
- •№1. Случайные события. Классификация. Действия над событиями.
- •№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
- •№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
- •№4. Теорема сложения. Следствия.
- •Теорема доказана.
- •№7. Формула полной вероятности и формула Байеса. Примеры.
- •№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
- •№9. Случайная величина. Функция распределения случайной величины и её свойства.
- •№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
- •№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
- •№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
- •№16. Нормальный случайный вектор.
- •№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
- •№20. Ряд распределения функции дискретной случайной величины.
- •№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.
- •24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.
- •№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.
- •№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.
- •№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.
- •№30. Точечные оценки и их свойства.
- •№31. Функция правдоподобия. Неравенство Рао-Крамера. Критерий эффективности Рао-Крамера.
- •№37. Критерий согласия . Пример.
№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
Условным законом распределения случайной величины, входящей в систему, называется её закон распределения, вычисленный при условии, что другая случайная величина приняла определённое значение.
Условные
функции распределения случайных величин
и
,
входящих в систему, обозначаются
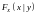 и
и
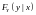 ,
а условные плотности распределения –
,
а условные плотности распределения –
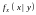 и
и
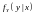 .
.
Теорема
умножения плотностей распределения:
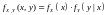 или
или
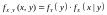 .
.
Для
независимых случайных величин
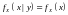 или
или
 .
.
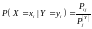 – условная вероятность.
– условная вероятность.
Случайные
величины
и
называют независимыми, если совместная
функция распределения
является произведением одномерных
функций распределения
 и
и
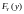 :
:
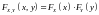 .
В противном случае случайные величины
называют зависимыми.
.
В противном случае случайные величины
называют зависимыми.
Для
независимых случайных величин
и
события
 и
и
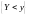 являются независимыми. Покажем, что
независимыми являются и все события
являются независимыми. Покажем, что
независимыми являются и все события
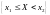 и
и
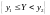 .
Действительно, в силу независимости
и
,
свойства 5 двумерной функции распределения
(
)
и свойства 3 одномерной функции
распределения (
)
имеем
.
Действительно, в силу независимости
и
,
свойства 5 двумерной функции распределения
(
)
и свойства 3 одномерной функции
распределения (
)
имеем
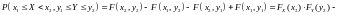
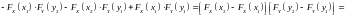
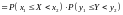 ,
что и означает независимость событий
и
.
,
что и означает независимость событий
и
.
Теорема:
Для того, чтобы непрерывные случайные
величины
и
были
независимыми, необходимо и достаточно,
чтобы для всех
и
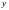
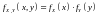 .
.
Доказательство:
I.
Необходимость.
Пусть случайные величины
и
независимы. Тогда, согласно определению
.
Имеем:
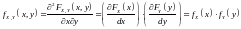 .
.
II.
Достаточность.
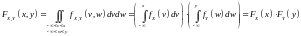 .
Теорема
доказана.
.
Теорема
доказана.
Теорема:
Дискретные случайные величины
и
являются
независимыми тогда и только тогда, когда
для всех возможных значений
и
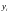
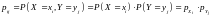 .
.
Случайные
величины
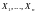 ,
заданные на одном и том же вероятностном
пространстве, называют независимыми в
совокупности, если
,
заданные на одном и том же вероятностном
пространстве, называют независимыми в
совокупности, если
 .
.
№18. Числовые характеристики случайного вектора.
Пусть
– случайный вектор, тогда
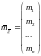 – математическое ожидание случайного
вектора
– математическое ожидание случайного
вектора
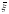 ,
,
 – его дисперсия.
– его дисперсия.
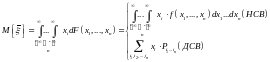
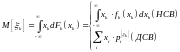
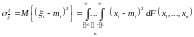
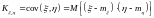 – ковариация (корреляционный момент)
– ковариация (корреляционный момент)

Свойства ковариации:
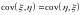 ;
;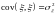 ;
;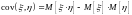
Доказательство:
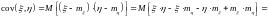
 ,
ч.т.д
,
ч.т.д
Если и независимы, то
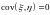 .
.
№19. Коэффициент корреляции и его свойства. Корреляционная матрица.
Коэффициентом
корреляции
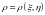 двух случайных величин
двух случайных величин
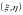 называется безразмерная величина
называется безразмерная величина
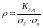 ,
где
,
где
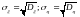 .
Коэффициент корреляции характеризует
степень тесноты линейной зависимости
между случайными величинами. Независимые
случайные величины являются
некоррелированными (для них
.
Коэффициент корреляции характеризует
степень тесноты линейной зависимости
между случайными величинами. Независимые
случайные величины являются
некоррелированными (для них
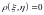 ).
).
Свойства:
 ;
;Если и независимы, то ;
 ,
при этом знак «плюс» нужно брать в том
случае, когда
,
при этом знак «плюс» нужно брать в том
случае, когда
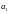 и
и
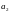 имеют одинаковые знаки, и минус – в
противном случае;
имеют одинаковые знаки, и минус – в
противном случае;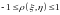 ;
;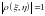 тогда
и только тогда, когда случайные величины
и
связаны линейной зависимостью (т.е.
тогда
и только тогда, когда случайные величины
и
связаны линейной зависимостью (т.е.
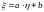 ).
).
Корреляционной
матрицей системы
случайных величин
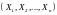 называется таблица, составленная из
корреляционных моментов всех этих
величин, взятых попарно
называется таблица, составленная из
корреляционных моментов всех этих
величин, взятых попарно
 ,
где
,
где
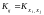 – корреляционный момент случайных
величин
– корреляционный момент случайных
величин
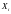 и
и
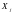 .
.
Корреляционная
матрица симметрична, поэтому обычно
заполняется лишь половина таблицы,
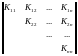 .
.
По
главной диагонали корреляционной
матрицы стоят дисперсии случайных
величин
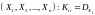 .
.
Нормированной
корреляционной матрицей системы
случайных величин называется таблица,
составленная из коэффициентов корреляции
всех этих величин, взятых попарно,
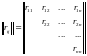 ,
где
,
где
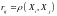 – коэффициент корреляции величин
и
.
По главной диагонали нормированной
корреляционной матрицы стоят единицы.
– коэффициент корреляции величин
и
.
По главной диагонали нормированной
корреляционной матрицы стоят единицы.
