Лабораторная работа № 7 Явление электромагнитной индукции. Исследование магнитного поля соленоида

0. I. Цель лабораторной работы

Выполнение лабораторной работы преследует следующие цели:

а) Экспериментальное изучение законов электромагнитной индукции

на конкретном примере образования и изменения магнитного поля внутри и вне соленоида.

б) Определение ёмкости …. двумя способами.

в) Обработка полученных результатов измерений на компьютере а также построение графических зависимостей с помощью электронных таблиц Excel.

г) Формулировка выводов по полученным результатам.

II. Теоретическая часть

1. Поток вектора В через поверхность. Для графического изобра­жения магнитного поля используют магнитные линии. Эти линии могут быть проведены через каждую точку пространства, в котором существу­ет магнитное поле, при этом вектор магнитной индукции В направлен по касательной к магнитной линии в любой ее точке.

Принято проводить линии гуще там, где поле сильнее, т. е. В боль­ше. Если принять густоту (количество линий, пересекающих поверхность площадью 1 м² перпендикулярно к ней) равной модулю вектора В, то мож­но определить численно поток вектора В через любую поверхность как количество линий пересекающих эту поверхность.

На рис. 1 магнитные линии пересекают две плоские площадки S_┴ и S, угол

между которыми равен α, (этот угол образуется также между норма­лью n и вектором В). Пусть эти площадки пересекает одинаковое количе­ство магнитных линий. Тогда поток через поверхность S_┴ равен численно Ф = N = 3 = B S_┴. Поток через поверхность S равен Ф = N = 3 = BS cos а (рис. 1 а). На рис. 1 б изображен вид со стороны магнитных линий.

Рис.1 Схема линий магнитного потока

2. Электромагнитная индукция. Закон Фарадея. В 1831 г. М. Фара­дей впервые обнаружил, что при изменении потока магнитной индукции через поверхность, ограниченную проводящим контуром, в нем возникает электрический ток. Это явление называют электромагнитной индукцией, а ток — индукционным.

Явление электромагнитной индукции свидетельствует о том, что при изменении магнитного потока в контуре возникает ЭДС индукции ε_i, при­чем она не зависит от способа изменения магнитного потока (изменение В, изменение S, поворот контура).

Закон фарадея имеет вид:

ε_i = -(dФ/dt) = - Ф. (1)

Знак «—» учитывает, что индукционный ток всегда направлен так, чтобы создаваемое им магнитное поле препятствовало изменению потока через поверхность контура (правило Ленца).

Для вычисления ε_i необходимо знать конкретный вид зависимости В(t).Вычисляя В, можно воспользоваться законом Био - Савара - Лапласа. В отдельных случаях специальной симметрии удобнее пользоваться тео­ремой о циркуляции вектора В.

Циркуляция В определяется как интеграл по контуру от скалярного произведение вектора В в произвольной точке и бесконечно малого пере­мещения dl от этой точки и обозначается как ∫В dl.

3. Теорема о циркуляции вектора В (для магнитного поля постоянных токов в вакууме). Циркуляция вектора В по замкнутому контуру Г равна произведению µ₀ на алгебраическую сумму токов I, пересекающих по­верхность контура Г:

∫В dl = µ₀∑I_i. (2)

Причем токи берутся со знаком «+», если их направления связаны с на­правлением обхода по контуру правилом правого винта и со знаком «—», если имеют противоположное направление (рис. 2).

Рис.2 Схема циркуляции вектора В по замкнутому контуру Г

4. Поле прямого тока. Используя теорему о циркуляции, удаётся вычислить поле прямого тока на расстоянии r от него.

Магнитные линии поля прямого тока представляют собой окружности в плоскости перпендикулярной проводу с током (рис 3). Поэтому в точках на этих окружностях поле одинаково по величине. Для контура, совпадающего с магнитной линией имеем:

∫В dl = 2πrB = µ₀∙I.

Из этого выражения получаем:

B = (µ₀∙I)/ 2πr.

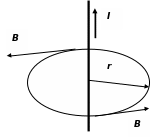
Рис.3 Магнитные линии поля прямого тока

5. Поле соленоида. Используя теорему о циркуляции, вычислим поле внутри соленоида. «Разрез соленоида» изображен на рис. 4. Из симметрии ясно, что поле внутри бесконечного (или тонкого по сравнению с длиной) соленоида однородно, а поле вне соленоида равно нулю. Взяв прямоуголь­ный контур со сторонами l и а, охватывающий области внутри и вне соле­ноида, напишем для него теорему о циркуляции:

∫В dl = В l + ВaCos(π/2) + 0∙l + ВaCos(π/2) = µ₀nlI,

откуда получаем:

Здесь n – число витков на единицу длины.

Рис.4 Схема «продольного разреза» соленоида