2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Первое: f1(x,y0)=0. Это дает одно из решений: y=y0=–2 – прямая, параллельная оси ОХ. Второе: f2(x0,y)=0 не добавляет решений: при фиксированном x=x0 переменная y остается произвольной.
a1. Учитывая, что теперь f2(x,y) ≠ 0, перепишем заданное ДУ: y′=2 .
a2. Применим преобразование: x=u+m; y=v+n, что определяет параллельный перенос системы координат XOY.
a3.
Выбираем числа: m, n
из системы:
Имеем: m=3,
n=–2.
Запишем обратное преобразование: u=x–3;
v=y+2
для использования при записи окончательного
выражения ответа.
a4.
Запишем преобразованное уравнение:
v′=
=2
=2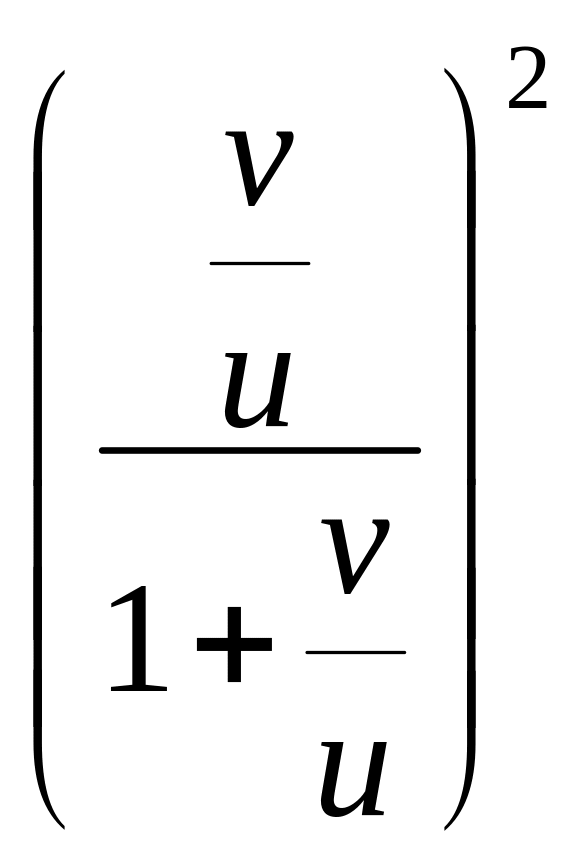
– однородное уравнение.
a5.
Примем
=z;
получим выражение: φ(z)=f(z)–z=–
.
a6. Проверим условие: φ(z0)= f(z0)– z0=0. Получаем решение: z=0, или v=0, или y+2=0, то есть прямая параллельная оси ОХ.
a7.
Учитывая, что теперь f(z)–z≠0,
запишем ДУ в виде: –
=
. (1)
a8.
Находим интеграл: J=–
=–
=–ln|z|–2arctgz.
a9.
Записываем результат интегрирования
уравнения (1):
–ln|z|–2arctgz=lnCu,
или в более удобной форме: –2arctgz=lnCuz
Записываем общее решение ДУ, учитывая
что z=
и u=x–3;
v=y+2
запишем: → –2arctg
=lnC(y+2).
Ответ: –2arctg =lnC(y+2) – общее решение ДУ, также y+2=0 (из общего не выделяется ни при каком значении С).
Пример 5–64: Решить дифференциальное уравнение: xy′=yln , y(1)=1.
Решение:
0). Представим ДУ в виде: y′ = ln . Деление на x≠0.
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «а» (см. Лекцию!):
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2. Примем = u; получим: φ(u)=f(u)–u=ulnu–u.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: невозможно!.
a4.
Учитывая, что теперь f(u)–u≠0,
запишем ДУ в виде (1):
=
.
a5. Интегрируем уравнение (1): ln|lnu–1|= lnCx, или lnu–1=Cx.
a6. Записываем общее решение. Учитывая что u= , получаем: ln =Cx+1.
a7.
Найдем частное решение: ln
=C1+1
→ C=–1
. Частное решение: ln
=1–x.
Ответ: Общее решение: ln =Cx+1; частное решение: ln =1–x.
Пример 6–173: Найти уравнение кривой, проходящей через точку (1,0), если длина отрезка оси абсцисс, отсекаемая её нормалью на 2 больше абсциссы точки касания.
В Примере 1–18 получены выражения: N=(х+yy′,0); – отсекаемого касательной на оси абсцисс, D =(х,0) – ординаты.
Р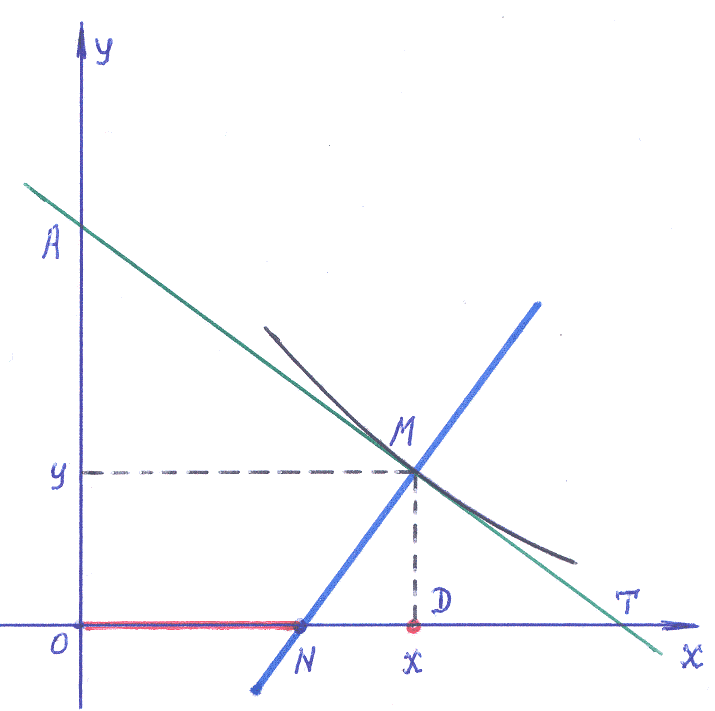
ешение:
Замечание: Условие задачи предполагает равенство величин: |ON|= (x+2).
Через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) с заданными свойствами, которые могут быть определены вариантами:
▪ [отрезок ОN]= [отрезок ОD+2] → х+yy′= х+2; (1)
▪ [отрезок ОN]=–[отрезок ОD+2]→ х+yy′=–(х+2).. (2)
Случай-1.
1). Запишем уравнение (1), в виде: yy′=2:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: их нет!
a2. Интегрируем уравнение (1): y2=4x+C– общее решение уравнения (1): семейство парабол
a3. Определим частное решение для точки А(1,0): C= –4, получаем: y2=4(x–1).
Случай-2.
2). Решим уравнение (2), записанное в виде: yy′=–2(х+1):
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: их нет!
a2. Интегрируем уравнение (1): y2= –2(х+1)2+C– общее решение уравнения (2): семейство концентрических окружностей с центром в точке (–1,0).
a3.
Определим частное решение для точки
А(1,0): C= 8,
получаем:
+
=1.
Ответ: Случай-1: y2=4(x–1). – частное решение; Случай-2: + =1 частное решение.
☻
Вопросы для самопроверки:
Какое уравнение называют дифференциальным?
Что такое решение ДУ, частное решение ДУ?
Что такое общее решение ДУ?
Что значит решить Задачу Коши?
Каковы стандартные формы однородных ДУ?
Какова стандартная схема решения однородных ДУ?
Какова стандартная форма уравнений, приводящихся к однородным ДУ?
< * * * * * >