
- •2). Данное уравнение решаем, применяя общий алгоритм «а» (см. Лекцию!):
- •2). Данное уравнение решаем, применяя общий алгоритм «в» (см. Лекцию!):
- •1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
- •2). Данное уравнение решаем, применяя общий алгоритм «а»:
- •3). В нашем случае:
- •1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
- •2). Данное уравнение решаем, применяя общий алгоритм «а»:
- •3). В нашем случае:
- •2). Данное уравнение решаем, применяя общий алгоритм «в» (см. 2-50):
- •2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
- •2). Данное уравнение решаем, применяя алгоритм «Случай-2» (см. Лекцию!):
- •2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
- •Домашнее задание
- •1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
- •2). Данное уравнение решаем, применяя общий алгоритм «а» (см. Лекцию!):
- •3). В нашем случае:
- •2). Данное уравнение решаем, применяя общий алгоритм «в» (см. Лекцию!):
- •1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
- •2). Данное уравнение решаем, применяя общий алгоритм «а» (см. Лекцию!):
- •3). В нашем случае:
- •2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
- •1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
- •2). Данное уравнение решаем, применяя общий алгоритм «а» (см. Лекцию!):
- •3). В нашем случае:
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «а»:
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2.
Примем
=
u; получим:
φ(u)=f(u)–u=u+![]() –u=
.
–u=
.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: u0= ±1, или y= ±x.
a4.
Учитывая, что теперь f(u)–u≠0,
запишем ДУ в виде (1):
![]() =
.
=
.
a5. Интегрируем уравнение (1): arcsinu=ln|x|+C, или u=sin(ln|x|+C).
a6. Записываем общее решение. Учитывая что u= , получаем: y=xsin(ln|x|+C).
Ответ: y=xsin(ln|x|+C) – общее решение ДУ, также y= ±x (из общего не выделяется).
Случай-2– x<0:
0). Представим ДУ в виде: y′ = – . Деление на x≠0.
1). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное!
2). Данное уравнение решаем, применяя общий алгоритм «а»:
3). В нашем случае:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0. Их нет.
a2. Примем = u; получим: φ(u)=f(u)–u=u– –u= – .
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Следует: u0= ±1, или y= ±x.
a4. Учитывая, что теперь f(u)–u≠0, запишем ДУ в виде (1): – = .
a5. Интегрируем уравнение (1): –arcsinu=ln|x|+C, или u=–sin(ln|x|+C).
a6. Записываем общее решение. Учитывая что u= , получаем: y=–xsin(ln|x|+C).
Ответ: y=–xsin(ln|x|+C) – общее решение ДУ, также y= ±x (из общего не выделяется).
Замечание: многие Случай-2 не выделяют (в шахматах это называют «зевок»!).
Пример 4–56: Решить дифференциальное уравнение: (x2 +y2)dy–2xydx=0.
Решение:
1). Признак, что задано однородное уравнение: множители при dx и dy – однородные функции 2-го порядка (одинакового!). Воспользуемся «стандартной схемой» решения.
2). Данное уравнение решаем, применяя общий алгоритм «в» (см. 2-50):
3). В нашем случае ДУ: (x2+y2)dy–2xydx=0.
a0. Выделяем возможные решения исходного уравнения f1(x,y)dx+f2(x,y)dy=0. Имеем: f1(x,y)= –2yx; f2(x,y)=(x2+y2). Первое дает решение: f1(x,y0)=0 при y0=0 – ось ОХ. Второе: f2(x0,y)=(x2+y2)≠0 при произвольных переменных!
a1.
Запишем наше уравнение в виде: y′=
=![]() =
=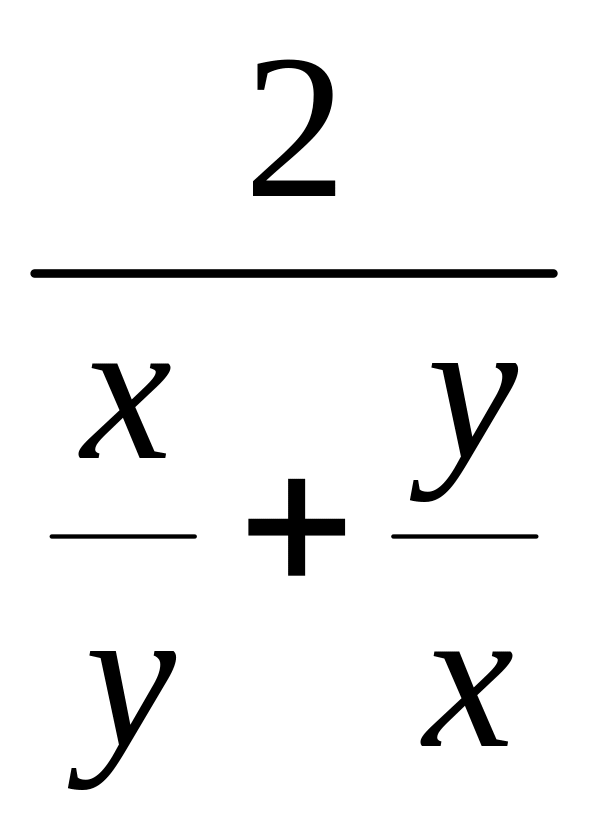 .
Здесь теперь учтено: f2(x,y)=
(x2+y2)
≠ 0 и x,y≠
0.
.
Здесь теперь учтено: f2(x,y)=
(x2+y2)
≠ 0 и x,y≠
0.
a2.
Примем
=
u; получим выражение:
φ(u)=f(u)–u=–![]() .
.
a3. Так как x,y≠ 0, то φ(u)≠0.
a4.
Учитывая, что теперь f(u)–u≠0,
записываем уравнение: –![]() =
. (1)
=
. (1)
a5.
Находим интеграл: J=–![]() → трудоемкий процесс!
→ трудоемкий процесс!
Так как исходная запись ДУ симметрична относительно переменных, то станем искать решение ДУ в виде функции: x=x(y). Алгоритм решения остаётся (с точностью до обозначений) прежним!
a1.
Запишем наше уравнение в виде: x′=![]() =
=![]() =
=![]() .
Здесь теперь учтено: x,y≠
0.
.
Здесь теперь учтено: x,y≠
0.
a2.
Примем
![]() =
u; получим выражение:
φ(u)=f(u)–u=–
=
u; получим выражение:
φ(u)=f(u)–u=–![]() .
.
a3. Проверим условие: φ(u0)=0. Имеем u0=±1, то есть y =± x – тоже решения.
a4.
Учитывая, что теперь f(u)–u≠0,
записываем уравнение: –![]() =
=![]() . (1)
. (1)
a5.
Находим интеграл: J=–![]() =–ln|u2–1|.
=–ln|u2–1|.
a6. Результат интегрирования уравнения (1): –ln|u2–1|=lnCy → (u2–1)y=C. Записываем общее решение ДУ. Учитывая что u = , получаем: y2– x2 =Cy.
Ответ: y2– x2 =Cy – общее решение ДУ, также y =± x (выделяется из общего при С=0).
Пример 5–59: Решить дифференциальное уравнение: (y+2)dx–(2x+y–4)dy =0.
Решение:
1).
Заданное ДУ – специального вида:
множители при dx
и dy
– линейные функции, их отношение образует
специальную дробь:
![]() .
Так как прямые l1:
0x+y+2=0
и l2:
2x+y–4=0
пересекаются: их нормальные векторы
.
Так как прямые l1:
0x+y+2=0
и l2:
2x+y–4=0
пересекаются: их нормальные векторы
![]() =(0,1)
и
=(0,1)
и
![]() =(2,1)
не коллинеарны, то имеем Случай-1 уравнения
специального вида. Далее используется
«стандартный алгоритм» для этого случая.
=(2,1)
не коллинеарны, то имеем Случай-1 уравнения
специального вида. Далее используется
«стандартный алгоритм» для этого случая.
