2). Данное уравнение решаем, применяя алгоритм «Случай-1» (см. Лекцию!):
a0. Выделяем возможные решения исходного уравнения y′= f(x,y). Нет таких: при фиксированном y=y 0 переменная x остается произвольной.
a1. Применим преобразование: x=u+m; y=v+n, что определяет параллельный перенос системы координат XOY.
a2.
Выбираем числа: m, n
из системы:
Имеем: m=–1,
n=–2.
Запишем обратное преобразование: u=x+1;
v=y+2
для использования при записи окончательного
выражения ответа.
a3.
Запишем преобразованное уравнение:
v′=
=tg
+
,
или v′= tg
+
–
однородное уравнение.
a4. Примем =z; получим выражение: φ(z)=f(z)–z=tg(z–2)+z–z= tg(z–2).
a6. Проверим условие: φ(z0)= f(z0)– z0=0. Получаем решения ДУ: z–2=πn, n Z, то есть z=2+πn, или v=u(2+πn), или y+2=(x+1)(2+πn), или y=x(2+πn)+πn – семейство прямых. При n=0 получаем выражение: y=2x – прямая, проходящая через начало координат. Замечание: подстановка y=2x в исходное ДУ подтверждает решение!
a7.
Учитывая, что теперь f(z)–z≠0,
запишем ДУ в виде:
=
. (1)
a8.
Находим интеграл: J=
=ln|sin(z–2)|.
a9.
Записываем результат интегрирования
уравнения (1):
ln|sin(z–2)|=lnCu,
или с учетом z: sin
=Cu.
Учитывая: u=x+1;
v=y+2,
записываем общее решение заданного ДУ:
sin
=C(x+1).
Ответ: sin =C(x+1) – общее решение ДУ, также y=x(2+πn)+πn, n Z.
Пример 8–177: Найти уравнение кривой, проходящей через точку (3,1), если длина отрезка, отсекаемого любой её касательной на оси ординат, равна поднормали.
В Примере 1–18 получены выражения: отрезка А=OА=(0,y–y′х), – отсекаемого касательной на оси ординат, ND =D–N=(x,0) – (х+yy′,0) =(–yy′,0) – поднормаль.
Решение:
1). Учитывая, что точка А может располагаться с точкой М по одну сторону от оси ОХ и по разные, запишем два варианта использования исходных данных:
▪ [отрезок ОА]= [отрезок ND] → y–y′х=yy′; (1)
▪ [отрезок ОА]= – [отрезок ND] → y–y′х=–yy′. (2)
С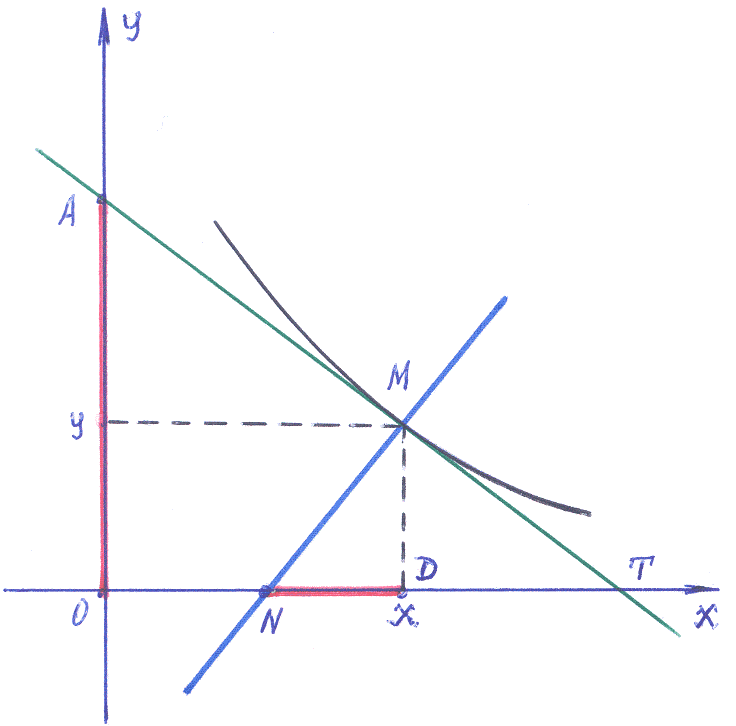
лучай-1.
2). Решим уравнение (1), записанное в виде: х′= +1:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: решение y0=0 геометрически тривиально!
a2. Примем =u; получим: f(u)–u=u+1–u=1.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Решений дополнительных нет.
a4. Учитывая, что f(u)–u≠0, запишем ДУ (1) в виде: du = . (3)
a5. Интегрируем уравнение (3): u= C+ lny.
a6.
Записываем общее решение ДУ. Учитывая
что u=
,
получаем: x= y(C+
lny), или y=С
–
общее решение уравнения (1).
Случай-2.
3). Решим уравнение (2), записанное в виде: х′= –1:
a1. Выделяем возможные решения исходного уравнения: f(x,y0)=0: решение y0=0 геометрически тривиально!
a2. Примем =u; получим: f(u)–u=u–1–u=–1.
a3. Проверим условие: φ(u0)= f(u0)–u0=0. Решений дополнительных нет.
a4. Учитывая, что f(u)–u≠0, запишем ДУ в виде (1): –du = . (4)
a5. Интегрируем уравнение (3): –u= lny+C, или (удобнее!): u =C– lny.
a6. Записываем общее решение ДУ. Учитывая что u= , получаем: x= y(C– lny).
4). Объединим результаты решения уравнений (1) и (2): x= y(C ± lny).
5). Выделим частное решение (интегральную кривую, проходящую через точку (3,1)):
3=1(C ± ln1) → C=3 → частное решение: x= y(3 ± lny).
Ответ: x= y(C ± lny) – общее решение ДУ; частное решение: x= y(3 ± lny).
Замечание: Нетрудно заметить совпадение результатов решения задачи в Примере 8–00 для Случая-2 и Случая-1 рассматриваемой задачи. По общим заданным свойствам семейства представленных кривых существенно отличаются, но решения совпадают!
* * * * * * * * * *