Суммы Дарбу. Их Свойства.

Определение:

Пусть ограничена на отрезке . Введём разбиение R этого отрезка.

R: , .

Тогда можем составить выражения:

- нижняя сумма Дарбу, - верхняя сумма Дарбу.

, .

Пусть ограничена на отрезке . Введём разбиение R этого отрезка.

R: , .

Тогда можем составить выражения:

- нижняя сумма Дарбу, - верхняя сумма Дарбу.

, .

Свойства сумм Дарбу:

1) , для одного и того же разбиения.

2) Рассмотрим два разбиения в случае, когда одно разбиение является продолжением другого. Т.е. - продолжение , если все точки являются точками .

Д обавление точек не увеличивает и не уменьшает . Пусть получается из добавлением одной точки.

, ,

,

,

Заметим, что если , то и . Отсюда заключаем:

, , , .

3) , ,

,

=> , т.е. .

- нижний интеграл (нижняя точная сумма Дарбу). .

- верхний интеграл (верхняя точная сумма Дарбу). .

.

Билет 40

Суммы Дарбу и интегрируемость функции по Риману.

Теорема:

Функция интегрируема на отрезке тогда и только тогда, когда .

Доказательство:

Докажем необходимость условия:

Функция интегрируема на отрезке .

Пусть , тогда , т.е. .

т.е. и .

Далее имеем: , т.е. .

Необходимость доказана.

Докажем достаточность условия:

.

.

.

Докажем, что .

,

,

, тогда , т.е. ,

.

Достаточность доказана.

Билет 41 Основная теорема о существовании определенного интеграла Римана.

Теорема (Основная)

Ограниченная функция f интегрируема на отрезке [a,b] тогда и только тогда, когда .

Доказательство:

П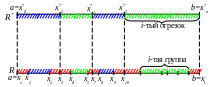 о теореме об интегрируемости (f интегрируема  ) функция интегрируема тогда и только тогда, когда (1). Надо доказать, что если . Т.е. если найдется одно R^*, удовлетворяющее неравенству (1), то оно (неравенство) будет выполняться для всех R. Возьмем произвольное . Нужно найти δ, такое чтобы выполнялось неравенство . По условию теоремы . Рассмотрим наше разбиение R^* и произвольное R, как показано на рисунке. Составим разность верхней и нижней сумм Дарбý для нового разбиения R: . Нужно сделать его меньше . Из условия имеем . Обозначим через Σ первую сумму и разобъем ее: Σ=Σ₁+Σ₂. Σ₁ – такие слагаемые, что элемент нового разбиения R содержит в себе хотя бы одну точку границы старого раазбиения R^*. Все остальное войдет в Σ₂. Рассмотрим отдельно Σ₁ и Σ₂:

Σ₁: т.к. функция f – ограничена (k - константа). Тогда (M и m – максимум и минимум на [a,b]). Получим Σ₁ , где λ_R<δ, а количество красных отрезков не превосходит 2n. Для того чтобы это неравенство выполнялось, достаточно взять δ< /8kn. Т.е. при δ< /8kn Σ₁< /2.

Σ₂: разобъем Σ₂ на повторные суммы, т.е. Σ₂=Σ(Σⁱ). Σⁱ≤ ≤ (M_i^*-m_i^*)ΣΔx_i^*, где M_j и m_j – максимум и минимум на j-том участке. Σⁱ – группировка тех новых j-тых участков, которые попали в один и тот же старый. Получим Σ₂ Σ₁+Σ₂<ε, т.е. Σ< . В итоге:

. Теорема доказана.

Следствие 1: Функция f – интегрируема на [a,b], если с : (если существует такая последовательность разбиений с мелкостью, стремящейся к нулю, что модуль разности последовательности интегральных сумм и интеграла стремится к нулю).

Следствие 2: Функция f – интегрируема на [a,b], если (если верхний интеграл равен нижнему).

Билет 42