§ 6. Однородные уравнения с постоянными коэффициентами

Рассмотрим теперь линейное однородное уравнение с постоянными коэффициентами

(17)

где постоянные числа. Мы покажем, что нахождение фундаментальной системы решений этого уравнения фактически сводится к решению алгебраического уравнения -й степени (квадратного при кубического при и т.д.).

Найдём вначале все решения этого уравнения, имеющие вид где Найдём производные этой функции: Подставим их в уравнение (16):

После сокращения на получим характеристическое уравнение

(18)

Случай 1. Предположим, что имеет место “самый хороший” случай: корни характеристического уравнения действительны и различны. Тогда уравнение можно считать решённым: действительно, в этом случае мы имеем линейно независимых функций являющихся решениями уравнения (16), а это означает, что , фундаментальная система решений этого уравнения. Следовательно, общее решение уравнения имеет вид

где произвольные константы.

Пример 1. Решить уравнение .

Решение. Полагая получим: откуда или Мы имеем две линейно независимые функции и удовлетворяющие уравнению, поэтому общее решение уравнения имеет вид

Случай 2. Если характеристическое уравнение имеет кратный корень , то, как будет показано ниже, решениями этого уравнения, наряду с функцией решениями этого уравнения будут также функции где кратность корня Докажем это.

Лемма. Пусть корень характеристического уравнения (18) и кратность этого корня. Тогда функции удовлетворяют уравнению (17).

Доказательство. Уравнение (17) запишем в виде где а Так как корень кратности то многочлен делится на т.е. где также многочлен от Выясним, как действует оператор на функцию Имеем:

и т.д.

Ясно, что при В частности, при а значит, Это показывает, что функция является решением уравнения (17). Лемма доказана.

Пример 2. Решить уравнение

Решение. Составим характеристическое уравнение: Разлагая левую часть на множители, получим: Отсюда Простой корень даёт функцию а двукратный корень – две функции: и Таким образом, – общее решение уравнения.

Завершим разбор ситуации, когда корни характеристического уравнения все являются действительными числами. Пусть корень кратности кратности , кратности Тогда Сумма равна степени многочлена поэтому где порядок данного уравнения. Функции

(19)

линейно независимы и являются (ввиду леммы) решениями уравнения (16). Так как количество этих функций равно то (19) – фундаментальная система решений уравнения

Случай 3. Перейдём теперь к рассмотрению случая, когда характеристическое уравнение имеет комплексные корни. Пусть комплексный корень этого уравнения. Функция – комплекснозначная функция действительного аргумента – является, очевидно, комплексным решением уравнения (17), но нам требуется найти действительные решения. Преобразуем эту функцию. Имеем:

где Проверим, что эти функции и сами являются решениями уравнения (17). Действительно, так как то Ввиду того, что многочлен с действительными коэффициентами, мы получаем:

В случае, когда комплексный корень кратности аналогичные рассуждения показывают, что функции удовлетворяют уравнению (17). Таким образом, комплексный корень кратности даёт линейно независимых решений уравнения (17). Причина того, что количество получаемых решений вдвое больше кратности корня состоит в том, что для числа и сопряжённого числа (которое обязательно тоже будет корнем характеристического уравнения) набор функций один и тот же.

Итак, рассмотрены все случаи, которые могут возникнуть при решении характеристического уравнения, и мы получаем теорему.

Теорема. Фундаментальная система решений уравнения -го порядка с постоянными коэффициентами состоит из ровно линейно-независимых функций – решений этого уравнения, причем если:

а) действительный корень кратности даёт решения

б) комплексный корень кратности ) дает решения ... ,

Пример 3. Проиллюстрируем теорему одним примером, а именно, найдём все решения уравнения Составим характеристическое уравнение: Его корни: Комплексными решениями уравнения являются функции и а их действительные и мнимые части образуют фундаментальную систему решений. Таким образом, общее решение уравнения имеет вид где произвольные константы .

В заключение этого параграфа разберём метод решения одного типа уравнений, сводящихся к уравнениям с постоянными коэффициентами. Однородным уравнением Эйлера называется уравнение вида

(20)

где действительные константы. Для решения этого уравнения введём новую независимую переменную полагая . Производные функции по надо теперь выразить через производные по Имеем:

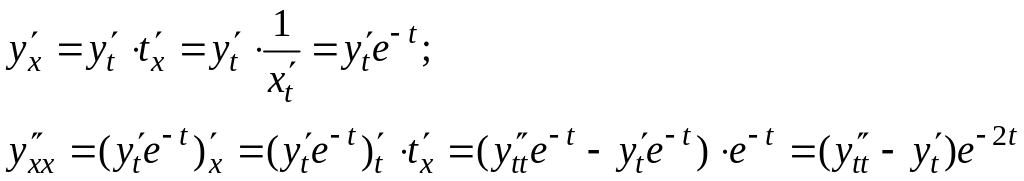
и т.д. Подставив эти выражения в уравнение (20), мы получим уравнение с постоянными коэффициентами. Заметим, что в области замена незаконна, но в этом случае можно сделать замену и уравнение (20) также сведётся к уравнению с постоянными коэффициентами.