
- •§ 6. Однородные уравнения с постоянными коэффициентами
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
- •§ 7. Линейные однородные системы с постоянными коэффициентами
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
- •§ 8. Линейные неоднородные уравнения и системы с постоянными коэффициентами со специальной правой частью
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
Разбор типовых примеров
Пример 1.
Найти все решения системы
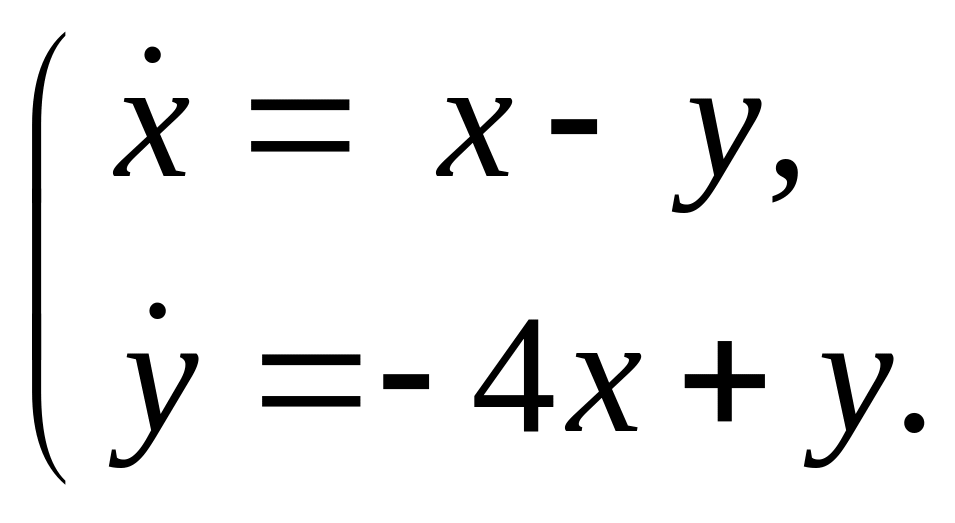
Решение.
Составим характеристическое уравнение:
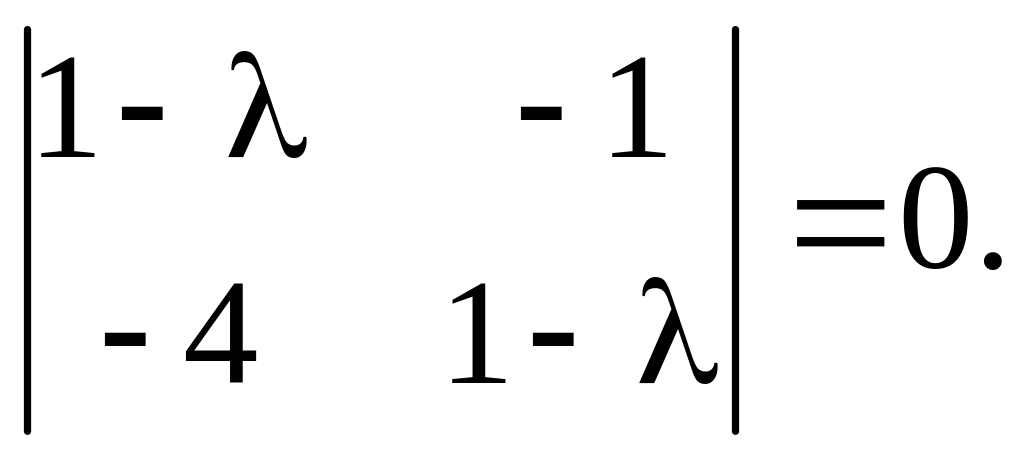 Его корни:
Его корни:
![]() Найдём собственные векторы из системы
Найдём собственные векторы из системы
![]() Для
Для
![]() имеем:
имеем:
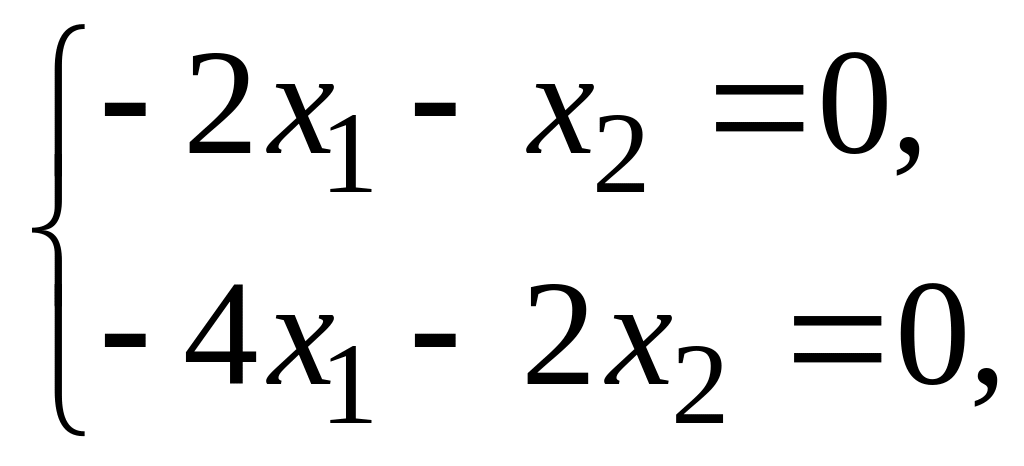 откуда
откуда
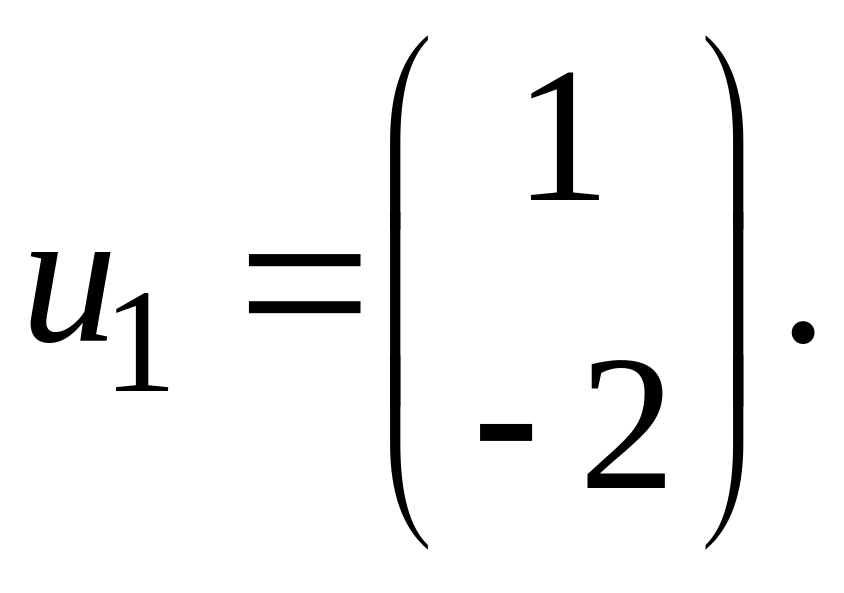 Для
Для
![]() имеем:
имеем:
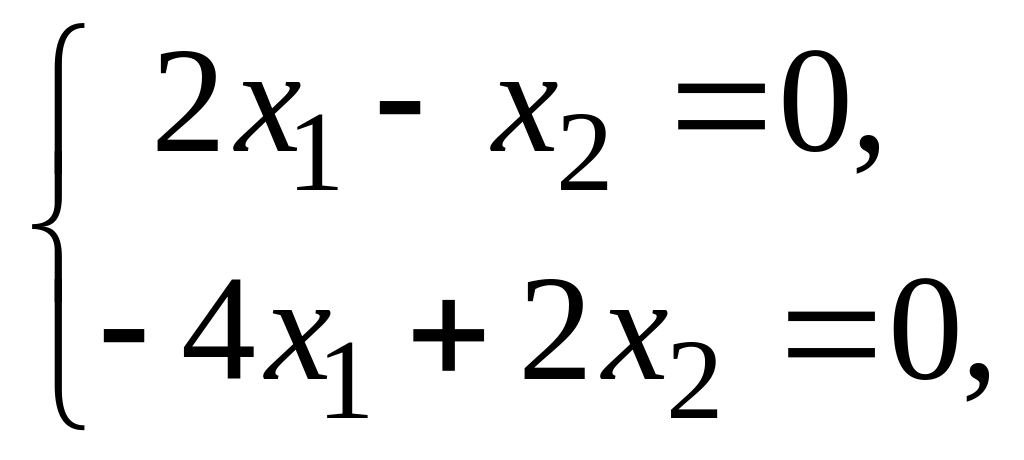 откуда
откуда
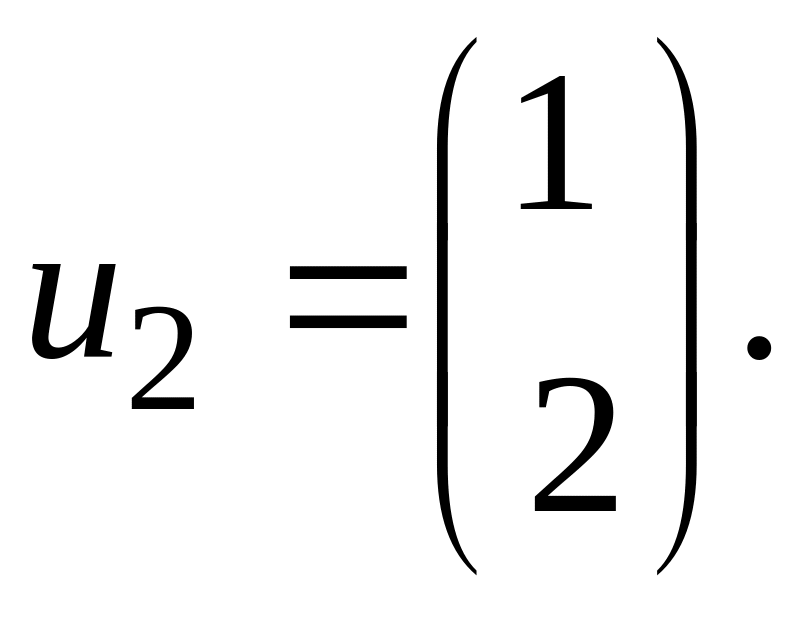
Таким образом, общее решение системы имеет вид
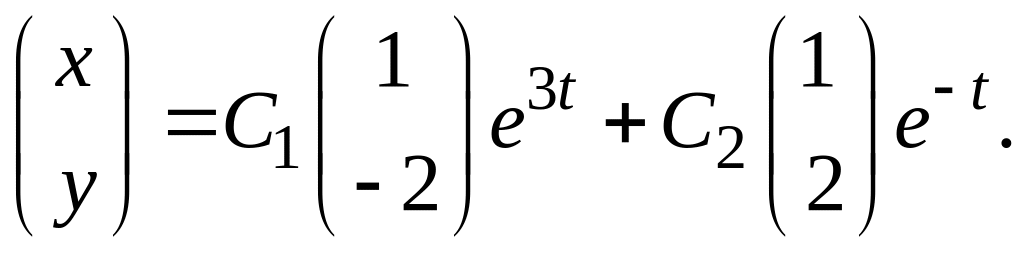
Пример 2.
Найти решение системы
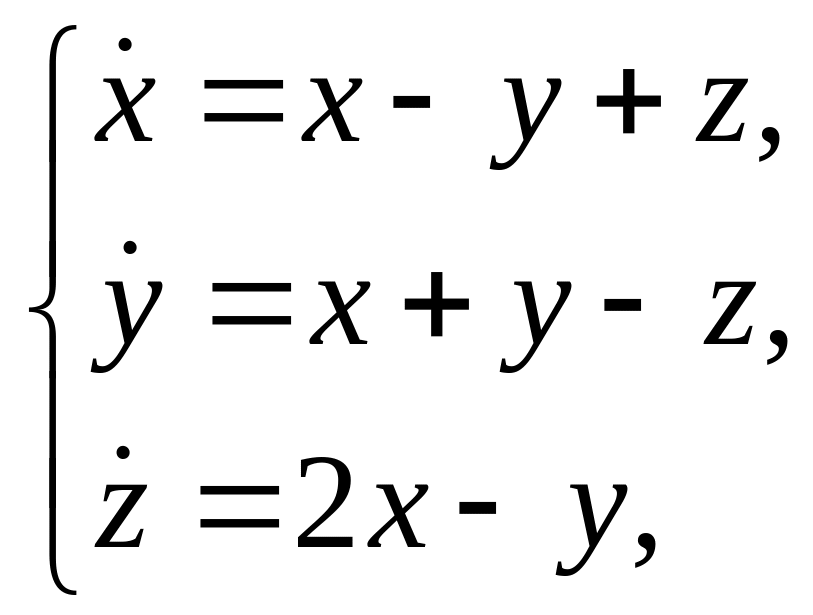 удовлетворяющее начальному условию
удовлетворяющее начальному условию
![]()
Решение.
Характеристическое уравнение
 имеет корни
имеет корни
![]()
![]()
![]() Для
имеем систему
Для
имеем систему
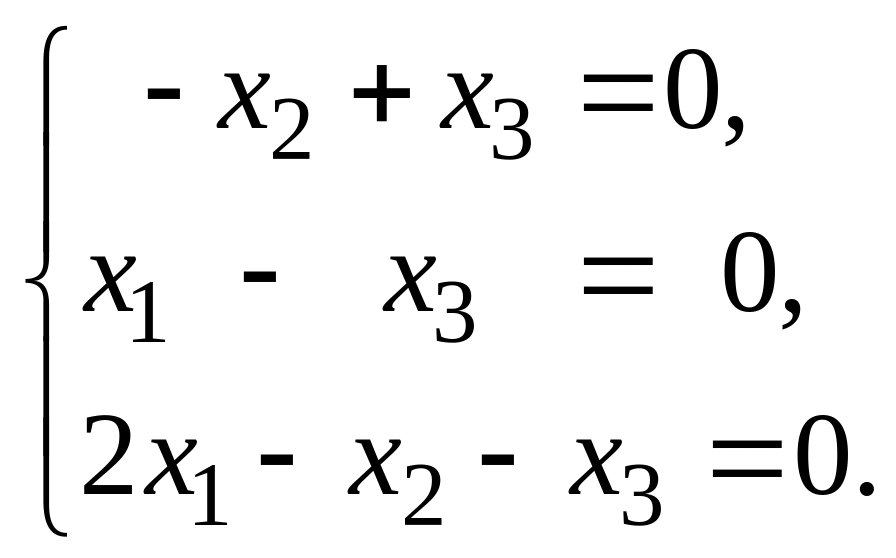 Её ненулевое решение:
Её ненулевое решение:
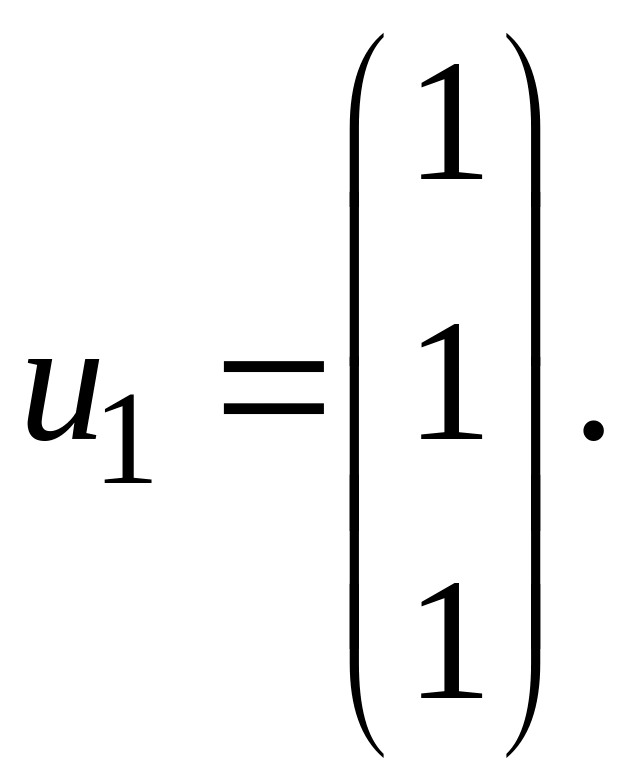 Для
имеем систему
Для
имеем систему
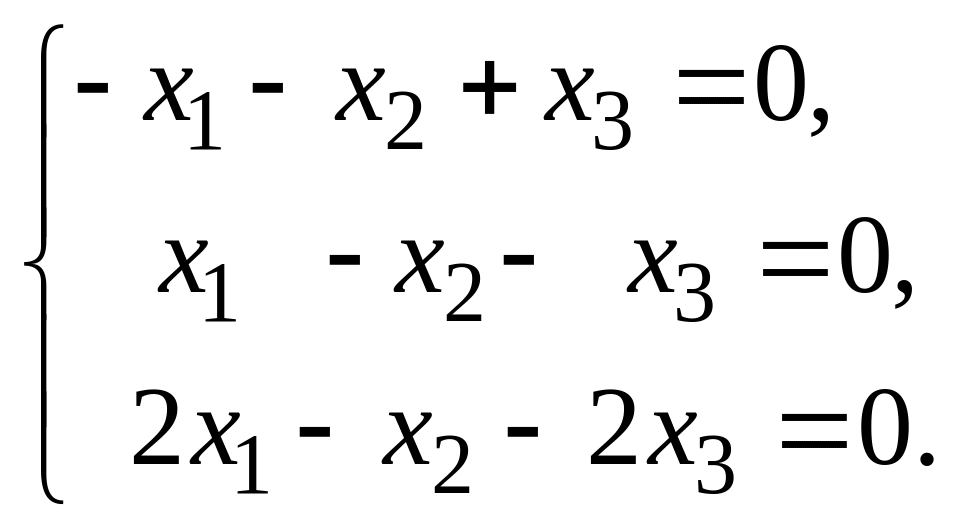 Её ненулевое решение:
Её ненулевое решение:
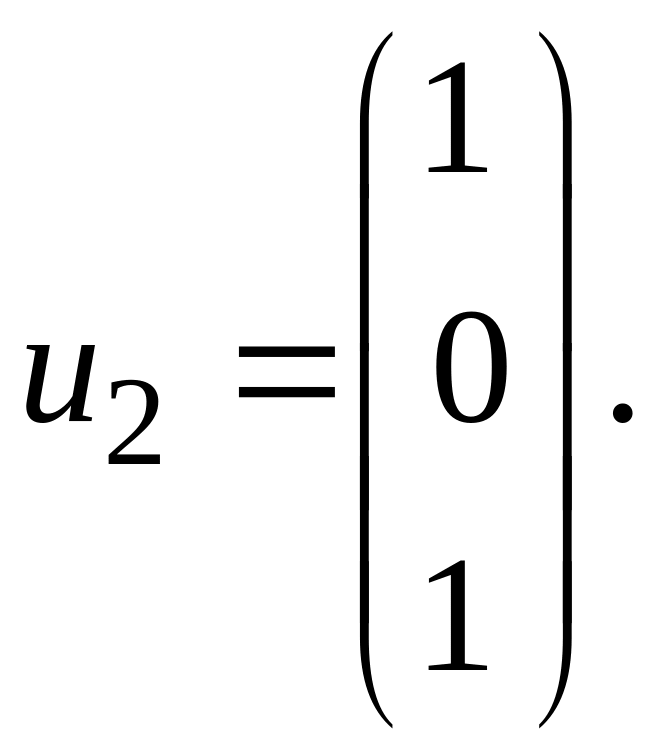 Наконец, для
имеем:
Наконец, для
имеем:
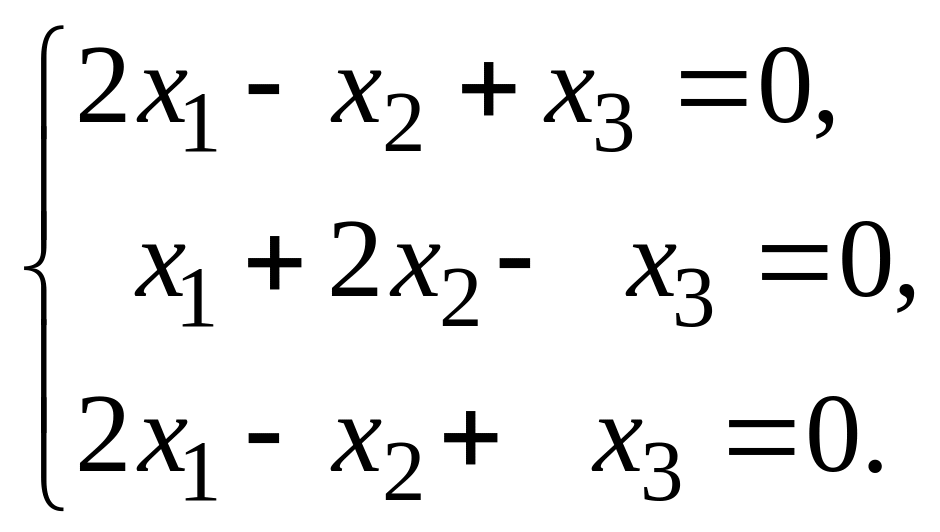 Её ненулевое решение:
Её ненулевое решение:
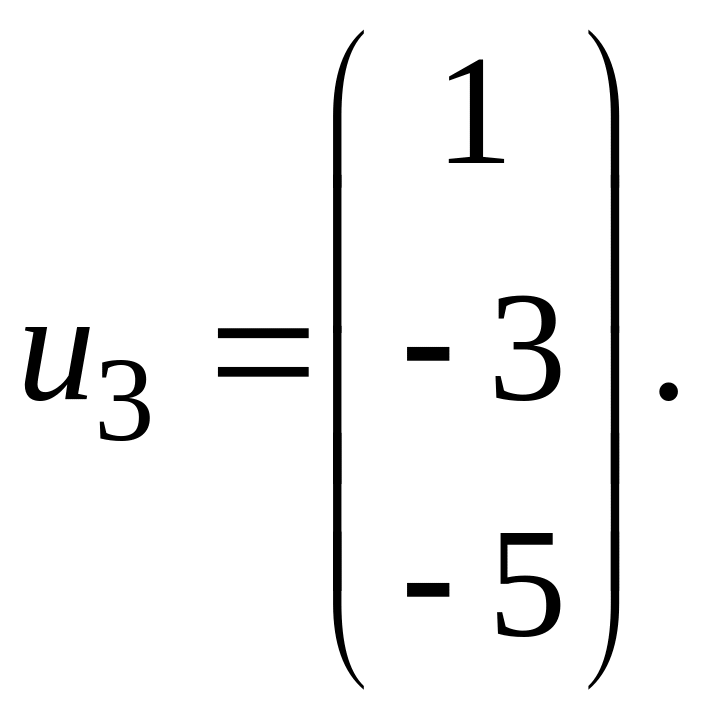 Таким образом, общее решение системы
имеет вид
Таким образом, общее решение системы
имеет вид
 Подставим в это равенство
Подставим в это равенство
![]() и воспользуемся начальным условием.
Тогда будем иметь
и воспользуемся начальным условием.
Тогда будем иметь
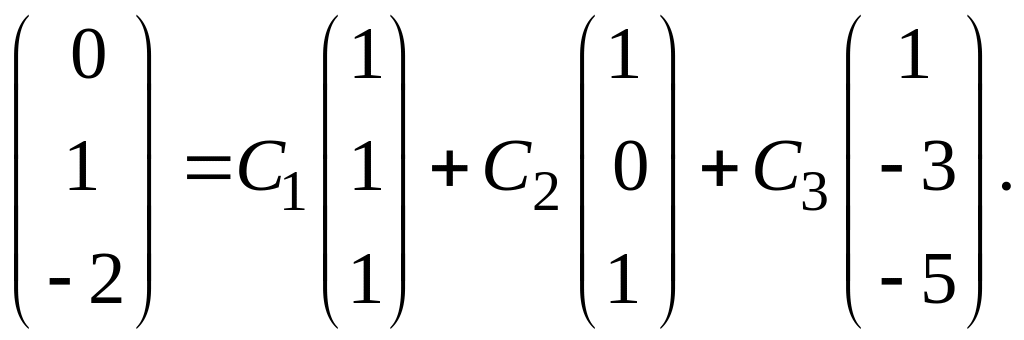
Мы получили систему
уравнений для нахождения
![]() Решив её, получим:
Решив её, получим:
![]()
![]()
![]() Отсюда получаем окончательный ответ:
Отсюда получаем окончательный ответ:
![]()
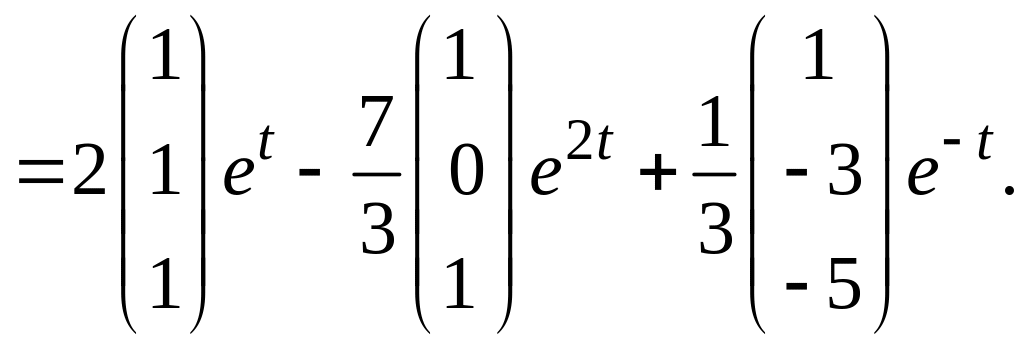
Пример 3.
Решить уравнение
![]() двумя способами: а) непосредственно и
б) сведением к системе. Сравнить полученные
решения.
двумя способами: а) непосредственно и
б) сведением к системе. Сравнить полученные
решения.
Решение.
Сначала решим это уравнение непосредственно.
Составим характеристическое уравнение:
![]() Его корни:
Его корни:
![]() Следовательно, общее решение уравнения
имеет следующий вид:
Следовательно, общее решение уравнения
имеет следующий вид:
![]()
Теперь сведём это
уравнение к системе. Положим
![]()
![]() Тогда
Тогда
![]() Значит, наше уравнение эквивалентно
системе
Значит, наше уравнение эквивалентно
системе
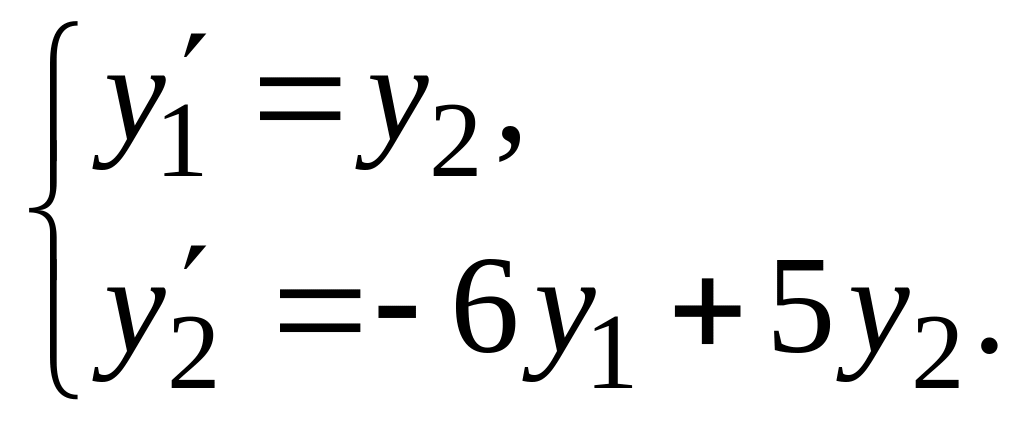 Матрица этой системы:
Матрица этой системы:
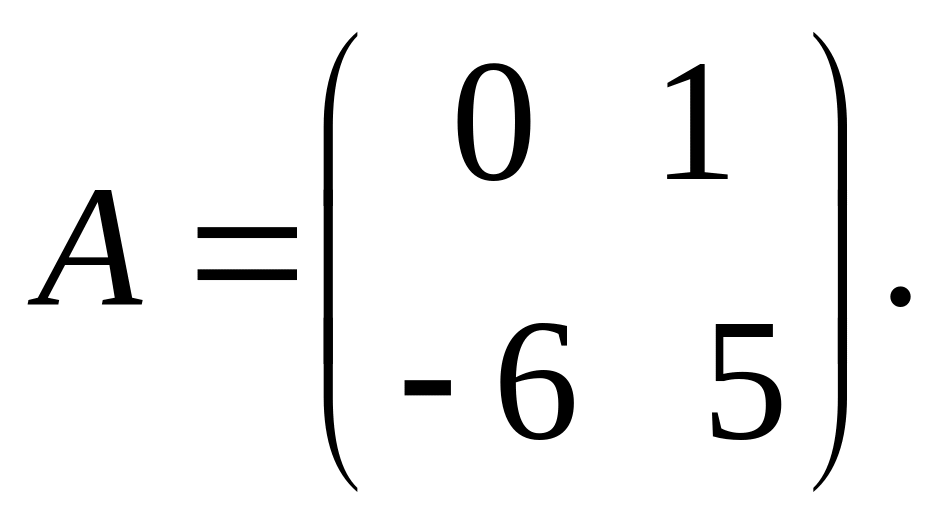 Характеристическое уравнение:
Характеристическое уравнение:
 Нетрудно видеть, что это уравнение
совпадает с характеристическим
уравнением, написанным ранее для
дифференциального уравнения. Для каждого
из корней характеристического уравнения
найдём соответствующий ему собственный
вектор. Если
Нетрудно видеть, что это уравнение
совпадает с характеристическим
уравнением, написанным ранее для
дифференциального уравнения. Для каждого
из корней характеристического уравнения
найдём соответствующий ему собственный
вектор. Если
![]() то мы получаем систему
то мы получаем систему
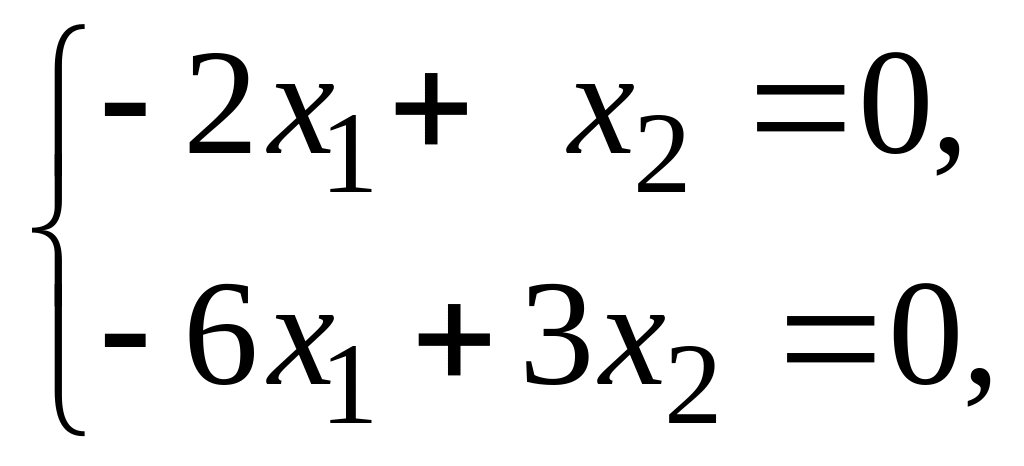 из которой находим собственный вектор
из которой находим собственный вектор
 Для корня
получаем систему
Для корня
получаем систему
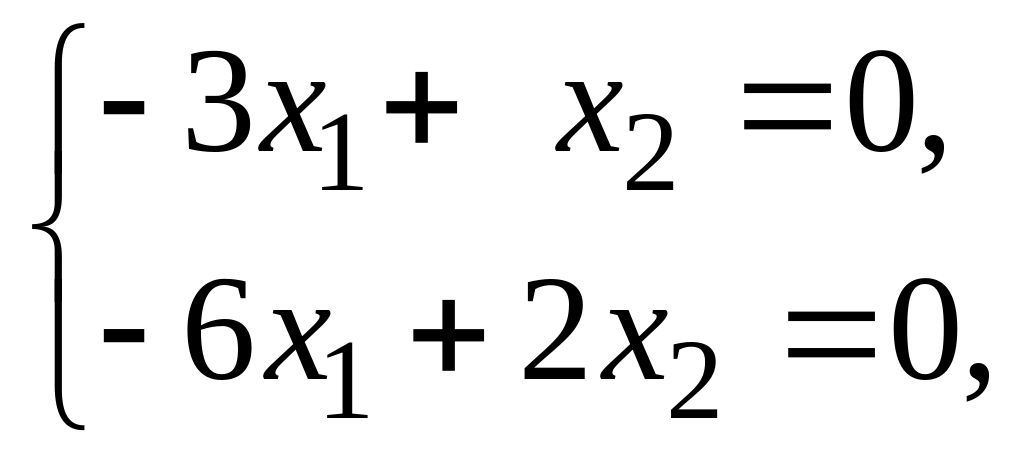 из которой находим
Отсюда следует, что общее решение системы
имеет вид
из которой находим
Отсюда следует, что общее решение системы
имеет вид
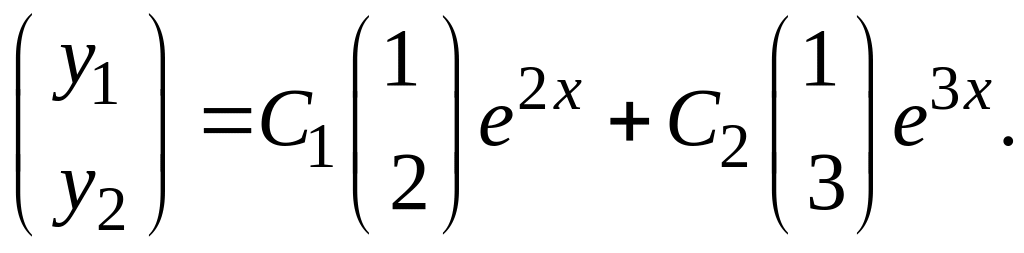 Взяв у векторов первые координаты,
получим:
Взяв у векторов первые координаты,
получим:
![]() Так как
Так как
![]() искомая функция, то мы получили общее
решение нашего уравнения:
Формула совпадает с той, которая была
получена непосредственным решением
уравнения.
искомая функция, то мы получили общее
решение нашего уравнения:
Формула совпадает с той, которая была
получена непосредственным решением
уравнения.
Пример 4.
Решить систему
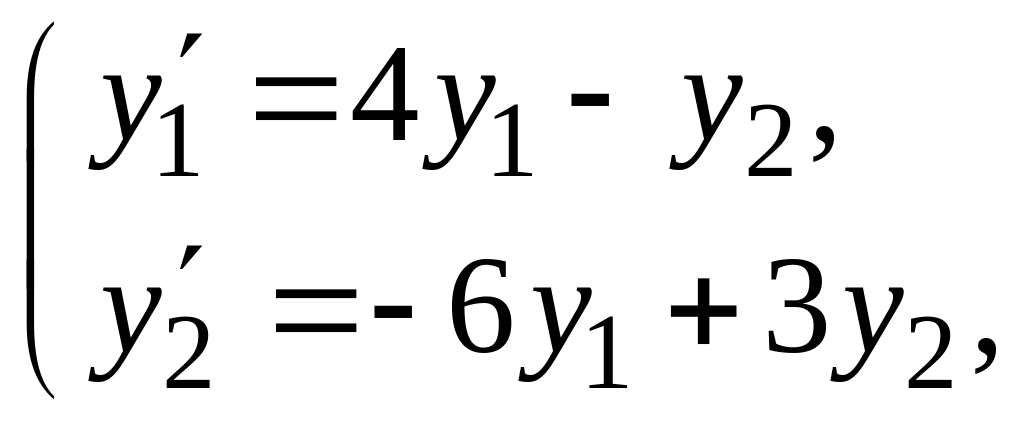 сведя её к одному уравнению второго
порядка.
сведя её к одному уравнению второго
порядка.
Решение.
Выразим
![]() из первого уравнения:
из первого уравнения:
![]() Подставим это выражение во второе
уравнение:
Подставим это выражение во второе
уравнение:
![]() откуда получаем для функции
откуда получаем для функции
![]() уравнение второго порядка:
уравнение второго порядка:
![]() Его характеристическое уравнение имеет
корни
Его характеристическое уравнение имеет
корни
![]() Следовательно,
Следовательно,
![]() Теперь находим функцию
Теперь находим функцию
![]()
![]()
Таким образом, общее решение системы имеет вид
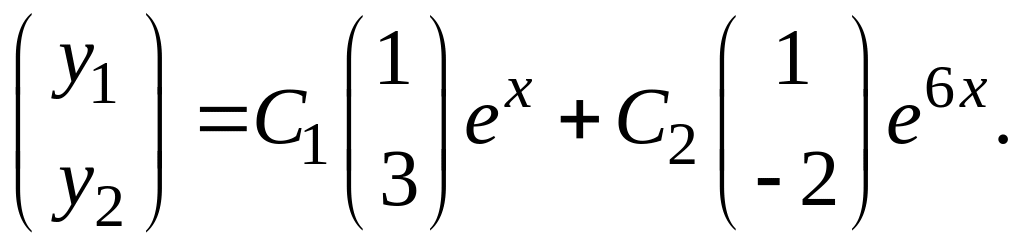
Замечание.
Не всякая система дифференциальных
уравнений сводится к одному уравнению.
Примером может служить система
![]()
![]() Однако, если, например, положить
Однако, если, например, положить
![]()
![]() то для функций
то для функций
![]() получится уравнение второго порядка:
получится уравнение второго порядка:
![]()
![]()
Задачи для самостоятельного решения
1. Найти все решения системы дифференциальных уравнений:
а)
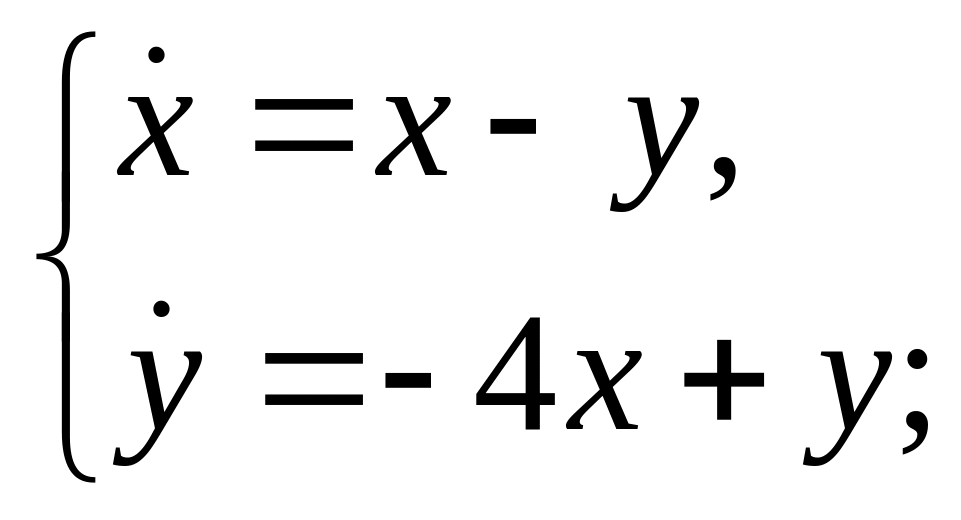 б)
б)
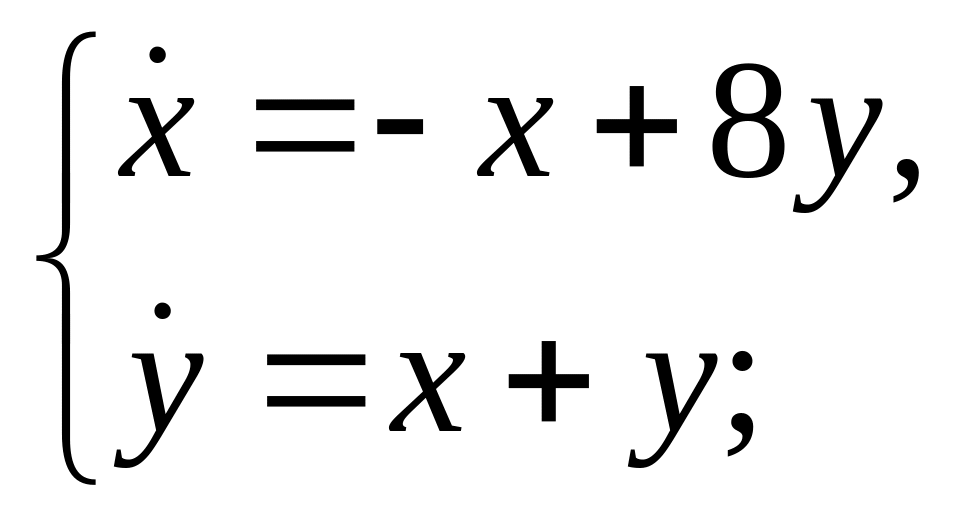 в)
в)
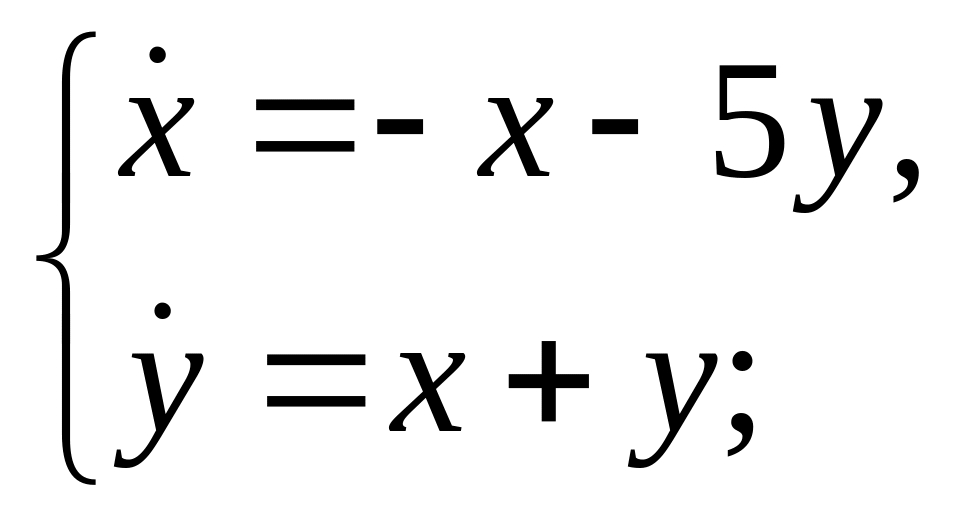
г)
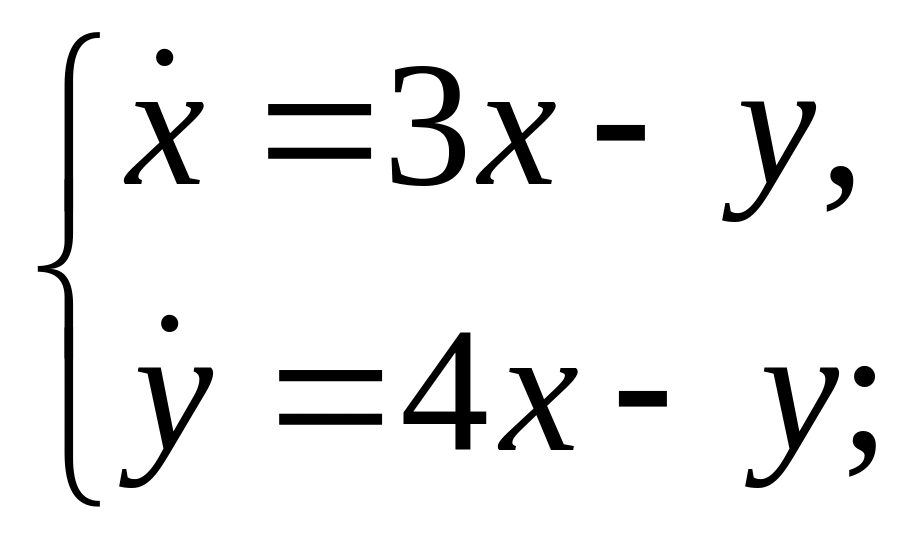 д)
д)
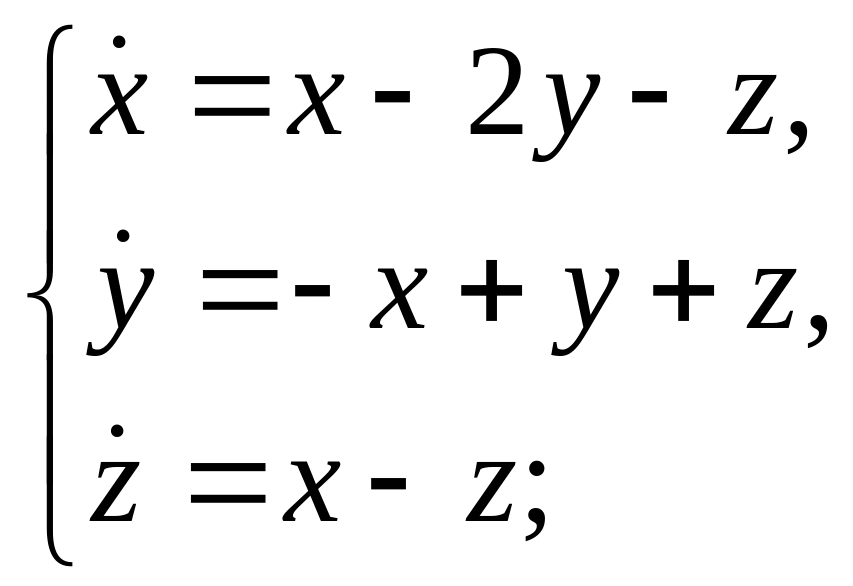 е)
е)
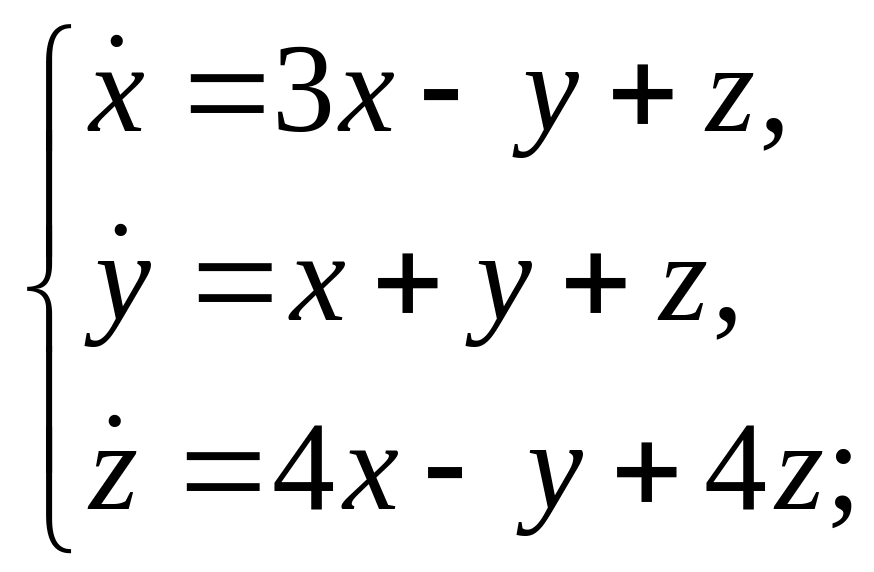
ж)
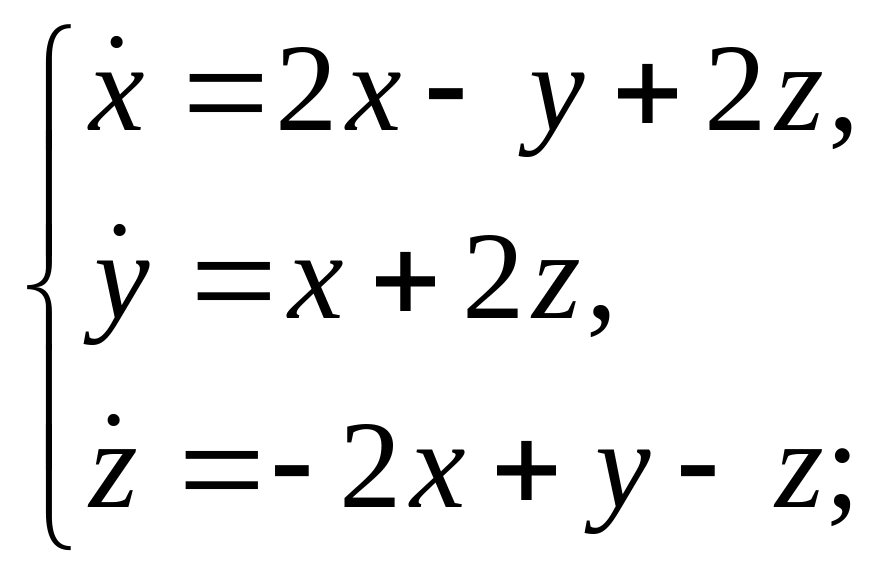 з)
з)
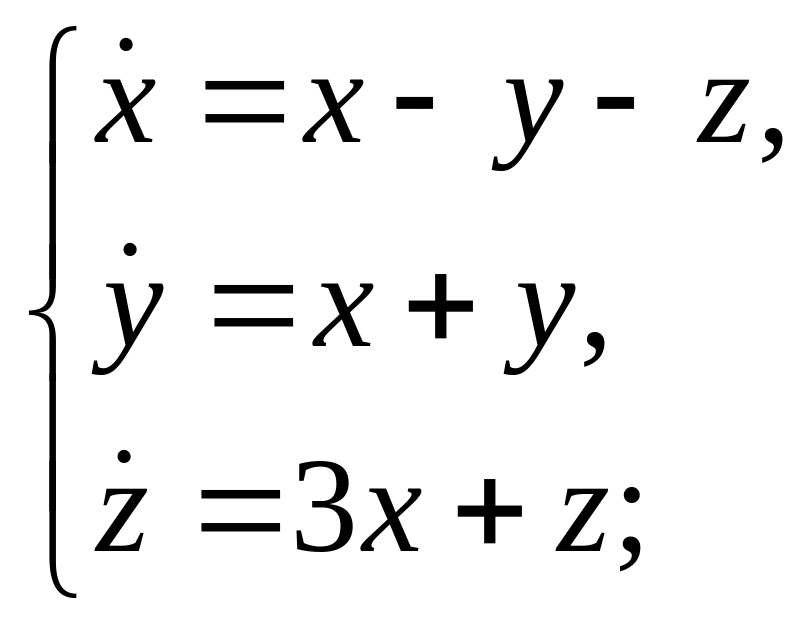 и)
и)
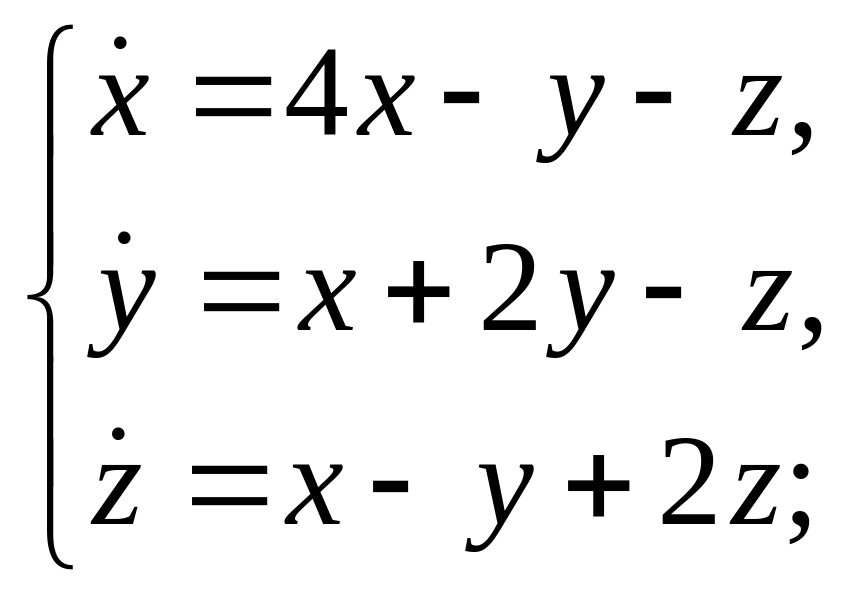
к)
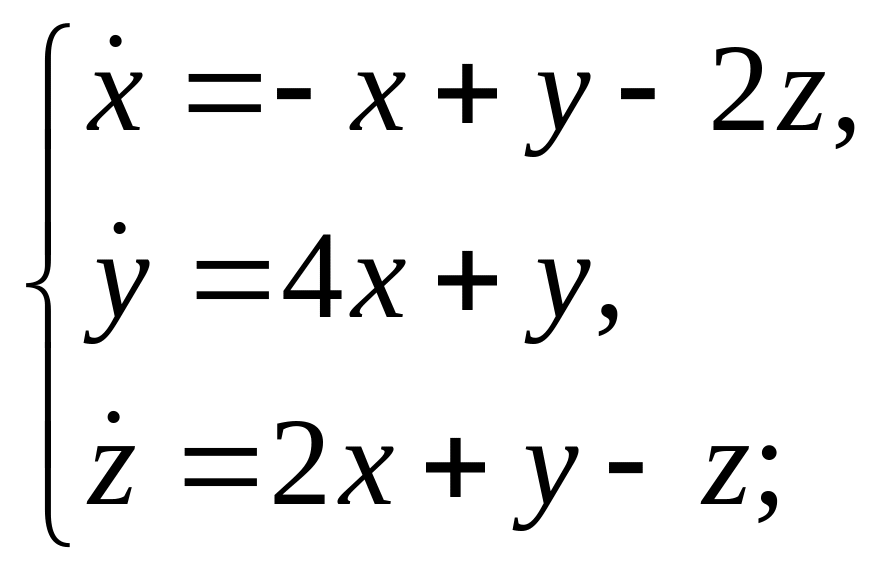 л)
л)
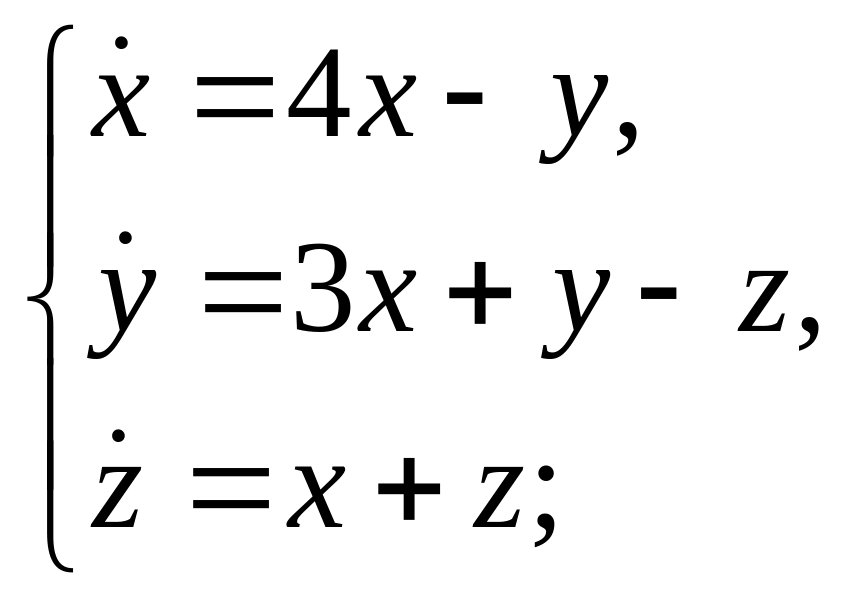 м)
м)
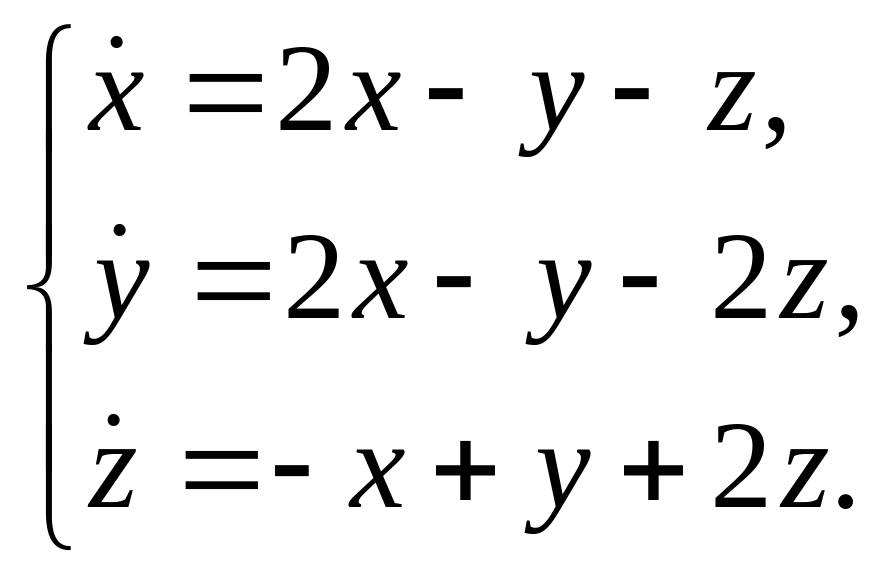
2.
Решить систему
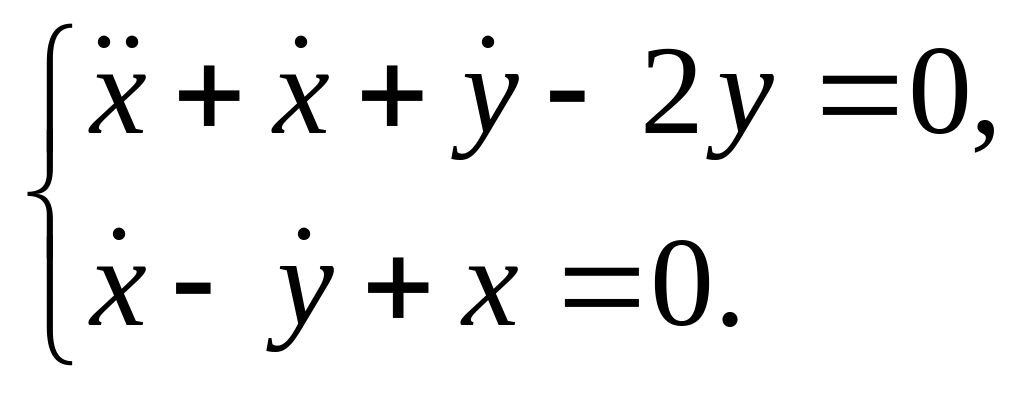
Ответы: 1. а)
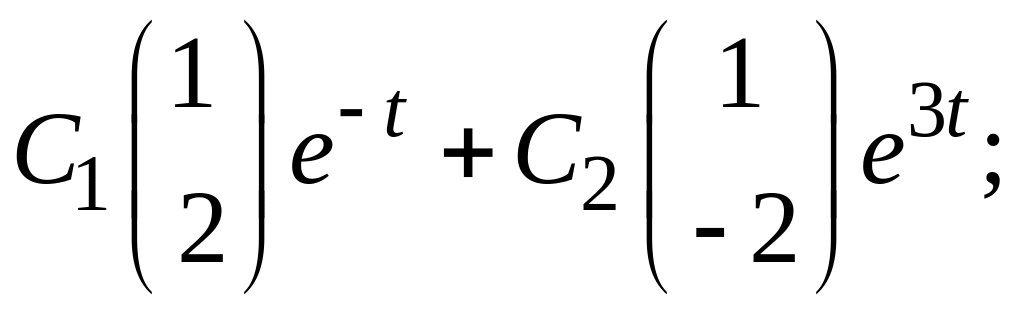 б)
б)
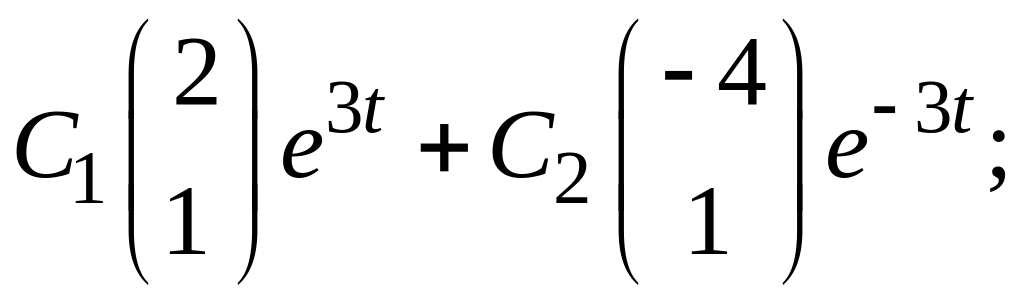 в)
в) 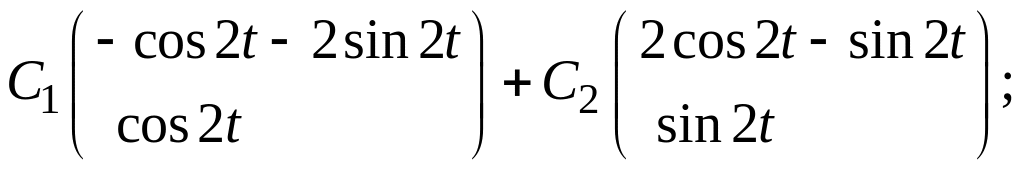 г)
г)
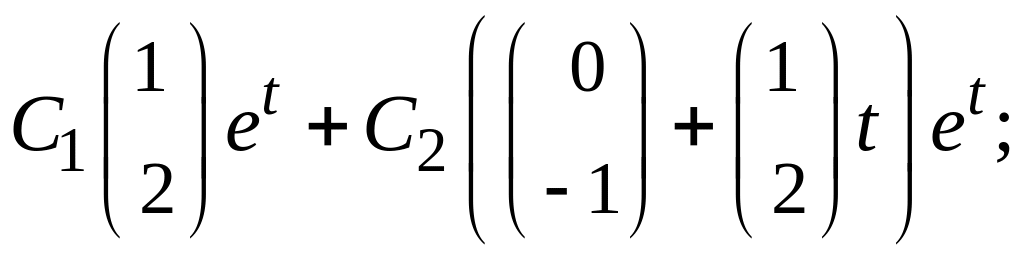 д)
д) 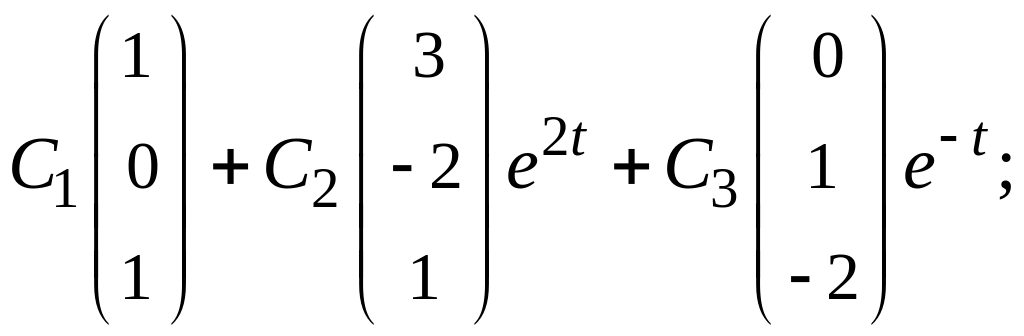 е)
е)
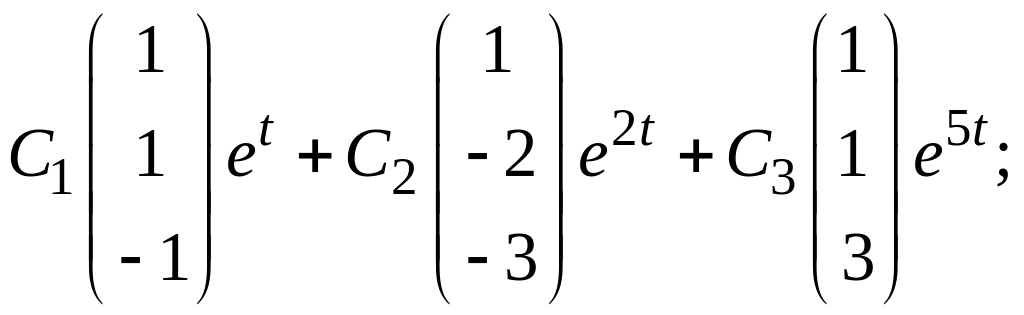 ж)
ж) 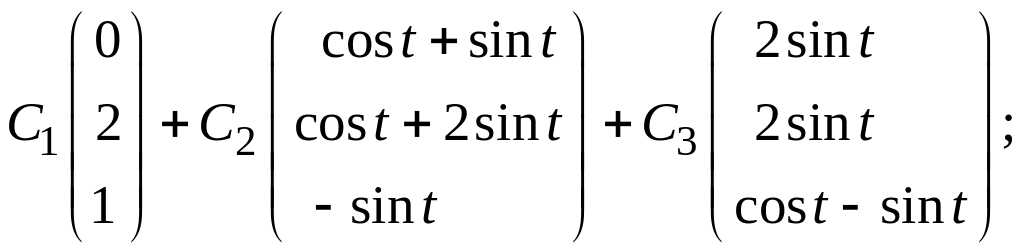 з)
з) 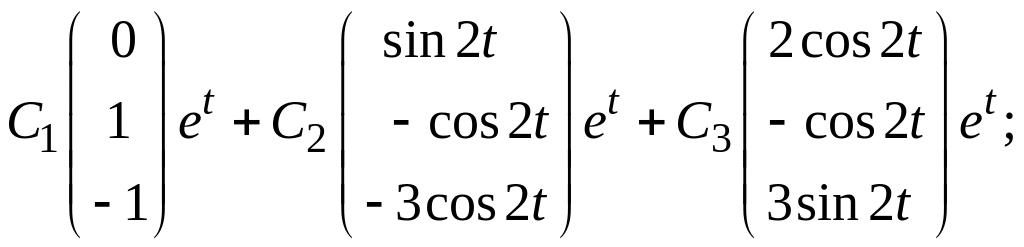 и)
и) 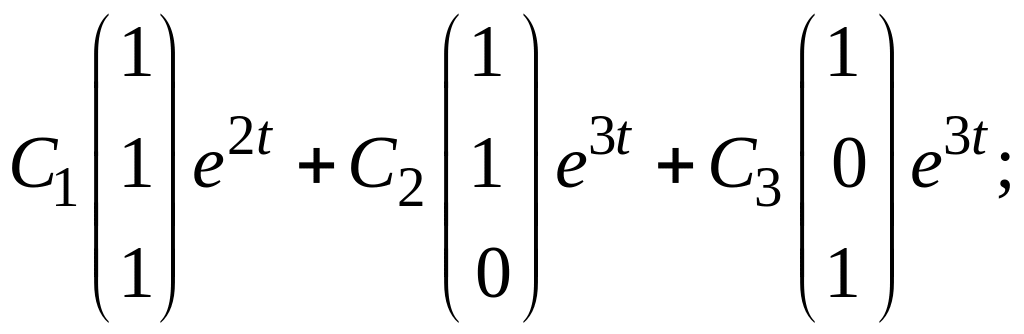 к)
к) ![]()
![]()
![]() л)
л) ![]()
![]()
![]() м)
м)
![]()
![]()
![]() 2.
2. ![]()
![]()
§ 8. Линейные неоднородные уравнения и системы с постоянными коэффициентами со специальной правой частью
Рассмотрим линейное неоднородное уравнение с постоянными коэффициентами
![]() (29)
(29)
В начале главы
было отмечено, что решение этого уравнения
будет получено, если удастся найти все
решения однородного уравнения
![]() и какое-либо (частное) решение уравнения
(29). Нахождение фундаментальной системы
решений однородного уравнения достаточно
подробно обсуждалось в предыдущих
параграфах, поэтому мы будем считать
её известной. Остаётся лишь найти частное
решение уравнения (29). Это может быть
сделано методом вариации постоянных
для любой функции
и какое-либо (частное) решение уравнения
(29). Нахождение фундаментальной системы
решений однородного уравнения достаточно
подробно обсуждалось в предыдущих
параграфах, поэтому мы будем считать
её известной. Остаётся лишь найти частное
решение уравнения (29). Это может быть
сделано методом вариации постоянных
для любой функции
![]() стоящей в правой части уравнения (29)
(единственным ограничением на функцию
является её непрерывность). Однако, если
имеет специальный вид, а именно, является
квазимногочленом,
то существует гораздо более эффективный,
чем метод вариации постоянных, способ
отыскания частного решения – это метод
неопределённых коэффициентов.
стоящей в правой части уравнения (29)
(единственным ограничением на функцию
является её непрерывность). Однако, если
имеет специальный вид, а именно, является
квазимногочленом,
то существует гораздо более эффективный,
чем метод вариации постоянных, способ
отыскания частного решения – это метод
неопределённых коэффициентов.
Назовём
квазимногочленом
функцию вида
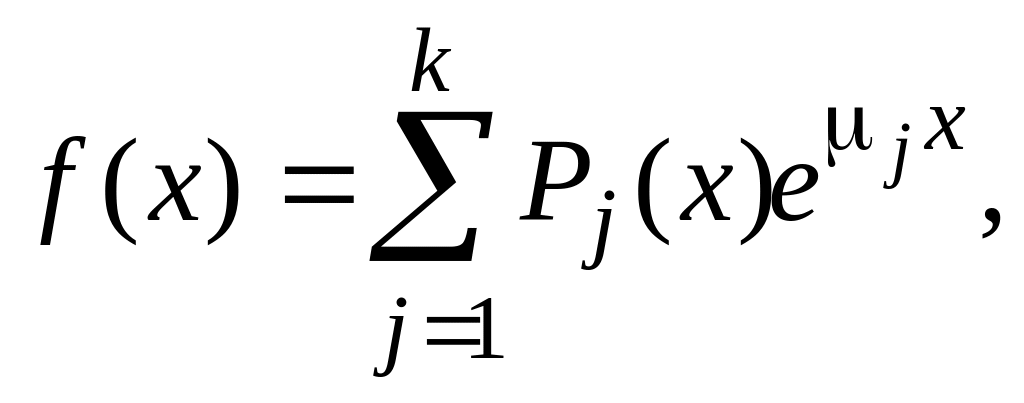 где
где
![]() обычный многочлен, а
обычный многочлен, а
![]() постоянные. При этом мы не исключаем
случай, когда числа
постоянные. При этом мы не исключаем
случай, когда числа
![]() комплексные. Так как
комплексные. Так как
![]() и
и
![]() то квазимногочленами оказываются
функции вида
то квазимногочленами оказываются
функции вида
![]()
![]()
![]()
![]() и т.д. Сделаем одно замечание.
и т.д. Сделаем одно замечание.
Замечание. Если уравнение (30) имеет вид
![]()
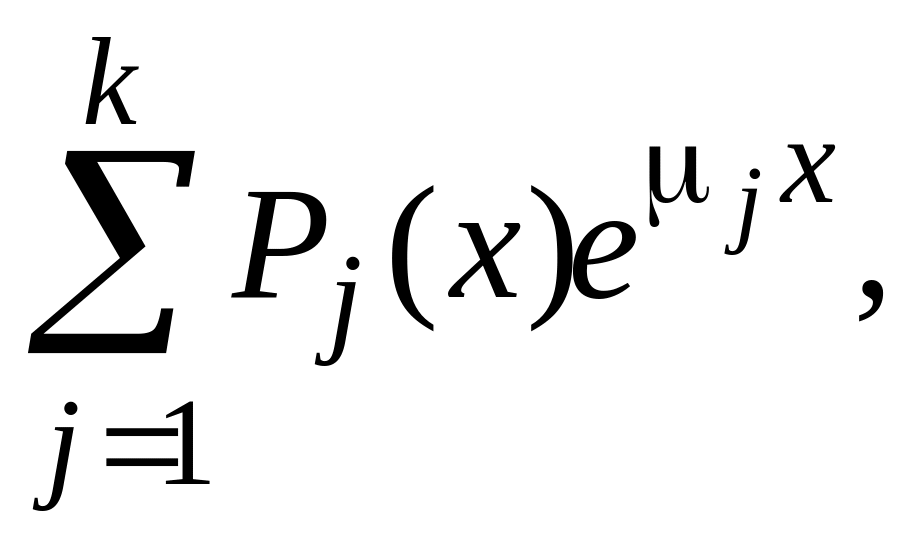 (30)
(30)
где
![]() дифференциальные операторы, то частное
решение уравнения (30) может быть
представлено в виде
дифференциальные операторы, то частное
решение уравнения (30) может быть
представлено в виде
![]()
где
![]() частное решение уравнения
частное решение уравнения
![]()
Доказательство высказанного утверждения очевидным образом следует из того факта, что линейный оператор.
Ввиду замечания нам достаточно научиться отыскивать частные решения уравнений вида
![]() (31)
(31)
Число
![]() может являться, а может и не являться
корнем характеристического уравнения
однородного уравнения
Если
не является корнем характеристического
уравнения, то будем говорить, что
может являться, а может и не являться
корнем характеристического уравнения
однородного уравнения
Если
не является корнем характеристического
уравнения, то будем говорить, что
![]() корень кратности 0. Таким образом,
корень кратности
многочлена
корень кратности 0. Таким образом,
корень кратности
многочлена
![]() в том и только том случае, если
в том и только том случае, если
![]() где
где
![]() многочлен, удовлетворяющий условию
многочлен, удовлетворяющий условию
![]() Ниже будет доказано, что уравнение (31)
обязательно имеет частное решение вида
Ниже будет доказано, что уравнение (31)
обязательно имеет частное решение вида
![]() (32)
(32)
где
кратность
в характеристическом уравнении, а
![]() степень многочлена
степень многочлена
![]() Используя
этот факт, можно сравнительно просто
найти частное решение уравнения
Используя
этот факт, можно сравнительно просто
найти частное решение уравнения
![]() Для этого достаточно равенство (32)
продифференцировать
раз и подставить производные в уравнение
(31). После подстановки мы получим систему
линейных алгебраических уравнений для
коэффициентов
Для этого достаточно равенство (32)
продифференцировать
раз и подставить производные в уравнение
(31). После подстановки мы получим систему
линейных алгебраических уравнений для
коэффициентов
![]() Решив её, найдём эти коэффициенты.
Решив её, найдём эти коэффициенты.
Теорема.
Линейное
уравнение с постоянными коэффициентами
![]() в котором
в котором
![]() многочлен, а
постоянная, имеет частное решение вида
многочлен, а
постоянная, имеет частное решение вида
![]() где
кратность
в характеристическом уравнении, а
степень многочлена
где
кратность
в характеристическом уравнении, а
степень многочлена
Доказательство теоремы мы не будем проводить во всех подробностях, а обрисуем лишь основные его этапы.
Обозначим через
![]() комплексное линейное пространство,
состоящее из всех линейных комбинаций
функций
комплексное линейное пространство,
состоящее из всех линейных комбинаций
функций
![]() Таким образом,
Таким образом,
![]() (здесь угловые скобки означают линейную
оболочку системы
векторов). Очевидно,
(здесь угловые скобки означают линейную
оболочку системы
векторов). Очевидно,
![]() базис пространства
базис пространства
![]() Рассмотрим два подпространства этого
пространства:
Рассмотрим два подпространства этого
пространства:
![]() и
и
![]() На пространстве
действует линейный оператор
переводя вектор
На пространстве
действует линейный оператор
переводя вектор
![]() в вектор
в вектор
![]() Так как
Так как
![]() то действие оператора
можно “расщепить” на два действия:
сначала оператором
то действие оператора
можно “расщепить” на два действия:
сначала оператором
![]() потом оператором
потом оператором
![]() Можно проверить, что оператор
Можно проверить, что оператор
![]() взаимно однозначно отображает пространство
взаимно однозначно отображает пространство
![]() на
на
![]() а оператор
а оператор
![]() взаимно однозначно отображает
взаимно однозначно отображает
![]() на
на
![]() Так как функция
Так как функция
![]() принадлежит подпространству
то она имеет прообраз
принадлежит подпространству
то она имеет прообраз
![]() при отображении
при отображении
![]() т.е.
т.е.
![]() Так как
Так как
![]() то
то
![]() имеет прообраз
имеет прообраз
![]() при отображении
т.е.
при отображении
т.е.
![]() Таким образом,
Таким образом,
![]() Так как
Так как
![]() то
то
![]() функция вида (32). Таким образом, уравнение
функция вида (32). Таким образом, уравнение
![]() имеет частное решение вида (32). Рассуждения
данной теоремы можно проиллюстрировать
следующим рисунком:
имеет частное решение вида (32). Рассуждения
данной теоремы можно проиллюстрировать
следующим рисунком:
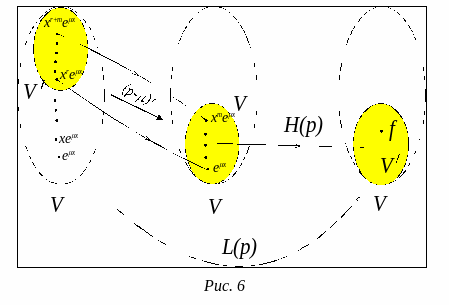
Утверждение,
аналогичное только что приведённой
теореме, справедливо для систем с
постоянными коэффициентами со специальной
правой частью. Отличие от уравнений
состоит в том, что вместо
![]() надо брать
надо брать
![]() Точное утверждение сформулируем в виде
теоремы, доказательство которой опустим.
Точное утверждение сформулируем в виде
теоремы, доказательство которой опустим.
Теорема.
Система
дифференциальных уравнений с постоянными
коэффициентами
![]() где
где
![]() постоянная
-матрица,
постоянная
-матрица,
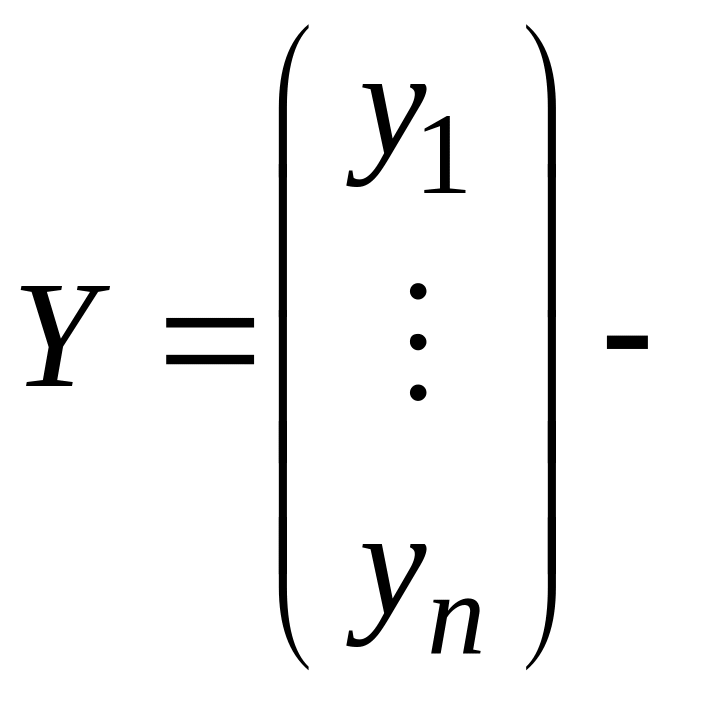 искомая вектор-функция, а
искомая вектор-функция, а
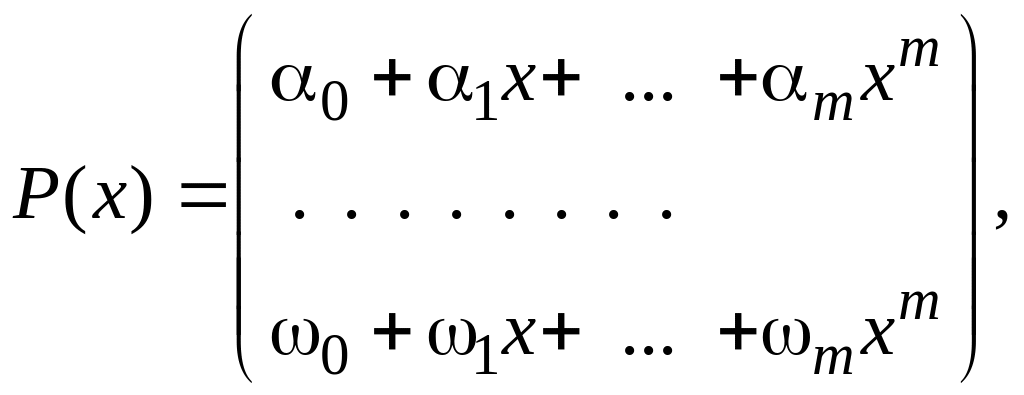 имеет частное решение вида
имеет частное решение вида
![]()
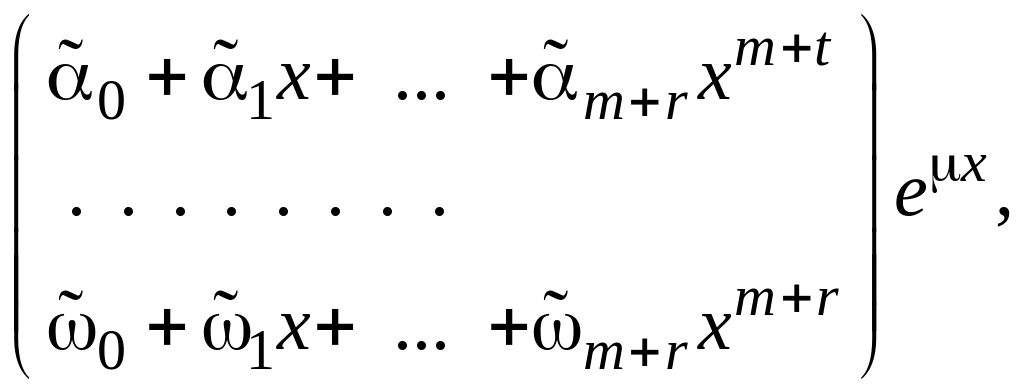 где
кратность
в характеристическом уравнении
где
кратность
в характеристическом уравнении
![]()
