
- •§ 6. Однородные уравнения с постоянными коэффициентами
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
- •§ 7. Линейные однородные системы с постоянными коэффициентами
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
- •§ 8. Линейные неоднородные уравнения и системы с постоянными коэффициентами со специальной правой частью
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
Разбор типовых примеров
Пример 1. Найти все решения уравнений:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() д)
д)
![]()
е)
![]() ж)
ж)
![]()
Решение.
а)
Составим характеристическое уравнение:
![]() Его корни:
Его корни:
![]() Следовательно, общее решение уравнения
имеет вид
Следовательно, общее решение уравнения
имеет вид
![]() где
где
![]() константы.
константы.
б)
Характеристическое уравнение:
![]() Его корни:
Его корни:
![]() Следовательно,
Следовательно,
![]()
в) Характеристическое
уравнение:
![]() т.е.
т.е.
![]() Корни:
Корни:
![]() Следовательно,
Следовательно,
![]()
г)
Здесь ищется функция
![]() Характеристическое уравнение:
Характеристическое уравнение:
![]() корни:
корни:
![]() Поэтому
Поэтому
![]()
д)
Имеем:
![]() Отсюда
Отсюда
![]() Базисные функции (т.е. функции, образующие
фундаментальную систему решений):
Базисные функции (т.е. функции, образующие
фундаментальную систему решений):
![]() и
и
![]() Следовательно,
Следовательно,
![]()
е)
Характеристическое уравнение:
![]() его корни:
его корни:
![]() Поэтому
Поэтому
![]()
ж)
Характеристическое уравнение:
![]() Его корни:
Его корни:
![]() Запишем число, стоящее под знаком корня,
в тригонометрической форме:
Запишем число, стоящее под знаком корня,
в тригонометрической форме:
![]() По формуле Муавра
По формуле Муавра
![]() где
где
![]()
Таким образом,![]()
![]()
![]()
![]()
Отсюда получается формула общего решения:
![]()
![]()
Пример 2. Составить дифференциальное уравнение, имеющее следующую фундаментальную систему решений:
а)
![]() б)
б)
![]() в)
в)
![]()
Решение.
а)
Корни характеристического уравнения
равны:
![]() Следовательно, характеристическое
уравнение имеет вид
Следовательно, характеристическое
уравнение имеет вид
![]() или
или
![]() Значит, дифференциальное уравнение
выглядит так:
Значит, дифференциальное уравнение
выглядит так:
![]()
б)
Здесь
![]() трёхкратный корень, поэтому
характеристическое уравнение имеет
вид
трёхкратный корень, поэтому
характеристическое уравнение имеет
вид
![]() или
или
![]() Следовательно, дифференциальное
уравнение имеет вид
Следовательно, дифференциальное
уравнение имеет вид
![]()
в)
Здесь
![]() поэтому характеристическое уравнение
имеет вид
поэтому характеристическое уравнение
имеет вид
![]() т.е.
т.е.
![]() Заменяя степени
на производные, получим дифференциальное
уравнение:
Заменяя степени
на производные, получим дифференциальное
уравнение:
![]()
Пример 3.
Решить уравнение Эйлера
![]()
Решение.
Положим
![]() Тогда
Тогда
![]()
![]() .
Подставив в уравнение, получим:
.
Подставив в уравнение, получим:
![]()
(здесь
![]()
![]() После упрощения будем иметь
После упрощения будем иметь
![]() Характеристическое уравнение
Характеристическое уравнение
![]() имеет корни
имеет корни
![]()
![]() Следовательно, общее решение имеет вид
Следовательно, общее решение имеет вид
![]() Возвращаясь к переменной
Возвращаясь к переменной
![]() получим:
получим:
![]() Такой же результат получается при замене
Такой же результат получается при замене
![]()
Пример 4.
Найти решения уравнений, удовлетворяющие
заданным начальным условиям: а)
![]()
![]()
![]() б)
б)
![]()
![]()
![]()
Решение.
а)
Составим характеристическое уравнение:
![]() Его корни:
Его корни:
![]() Общее решение уравнения:
Общее решение уравнения:
![]() Подставим в эту формулу
Подставим в эту формулу
![]()
![]() Найдём производную:
Найдём производную:
![]() Так как
Так как
![]() то мы получаем:
то мы получаем:
![]() Следовательно,
Следовательно,
![]() Отсюда
Отсюда
![]()
б)
Характеристическое уравнение:
Корни:
![]() Общее решение уравнения:
Общее решение уравнения:
![]() Так как
то
Так как
то
![]() Значит,
Значит,
![]() Дифференцируем:
Дифференцируем:
![]()
![]() Подставим начальные условия.
Подставим начальные условия.
![]()
![]() Таким образом,
Таким образом,
![]()
![]() Значит,
Значит,
![]() .
.
Задачи для самостоятельного решения
1. Найти все решения уравнения:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]()
ж)
![]() з)
з)
![]()
и)
![]() к)
к)
![]()
л)
![]() м)
м)
![]()
н)
![]() о)
о)
![]()
п)
![]()
2. Составить дифференциальное уравнение с постоянными коэффициентами, для которого данное множество функций является фундаментальной системой решений:
а)
![]() б)
б)
![]() в)
в)
![]()
3. Решить уравнение методом вариации постоянных:
а)
![]() б)
б)
![]()
в)
![]()
4. Найти решение уравнения, удовлетворяющее заданному начальному условию:
а)
![]()
![]()
б)
![]()
![]()
5. Решить однородные уравнения Эйлера:
а)
![]() б)
б)
![]()
в)
![]()
6.
Решить уравнение, считая
![]() известной функцией:
известной функцией:
а)
![]() б)
б)
![]()
7.
Найти решения уравнения, ограниченные
при
![]()
а)
![]() б)
б)
![]()
Ответы: 1. а)
![]() б)
б)
![]() в)
в)
![]() г)
г) ![]() д)
д)
![]() е)
е)
![]() ж)
ж) ![]() з)
з)
![]() и)
и)
![]() к)
к) 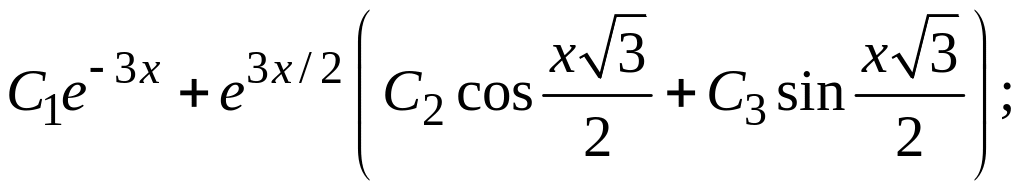 л)
л) ![]() м)
м) ![]() н)
н) ![]() о)
о)![]() п)
п) ![]() 2. а)
б)
2. а)
б) ![]() в)
в)
![]() 3. а)
3. а) ![]() б)
б) ![]()
![]() в)
в) ![]() 4. а)
4. а)
![]() б)
б) ![]() 5. а)
5. а)
![]() б)
б)
![]() в)
в) ![]() 5. а)
5. а) ![]() б)
б) ![]() 6. а)
6. а) ![]() б)
б) ![]()
