
- •Глава IV. Линейные дифференциальные уравнения и системы § 1. Общие замечания. Однородные и неоднородные уравнения и системы
- •§ 2. Фундаментальная система решений однородной системы и однородного уравнения
- •§ 3. Дифференцирование векторов, матриц, определителей. Комплекснозначные функции действительного аргумента
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
- •§ 4. Определитель Вронского
- •§ 5. Метод вариации постоянных для неоднородных уравнений и систем
- •Разбор типовых примеров
- •Задачи для самостоятельного решения
Глава IV. Линейные дифференциальные уравнения и системы § 1. Общие замечания. Однородные и неоднородные уравнения и системы
Линейным
дифференциальным уравнением
![]() -го
порядка
называется уравнение вида
-го
порядка
называется уравнение вида
![]() (1)
(1)
где
![]() непрерывные на некотором отрезке
непрерывные на некотором отрезке
![]() функции.
функции.
Системой линейных дифференциальных уравнений первого порядка называется система
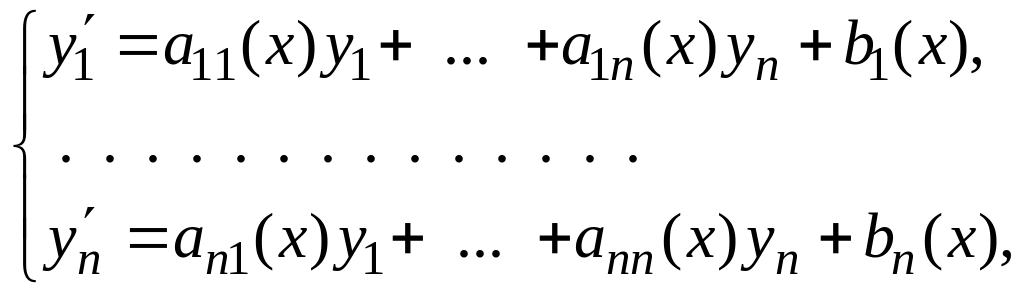 (2)
(2)
где
![]() непрерывные на отрезке
функции. Система (2) может быть записана
в матричной форме:
непрерывные на отрезке
функции. Система (2) может быть записана
в матричной форме:
![]() (3)
(3)
где матрицы
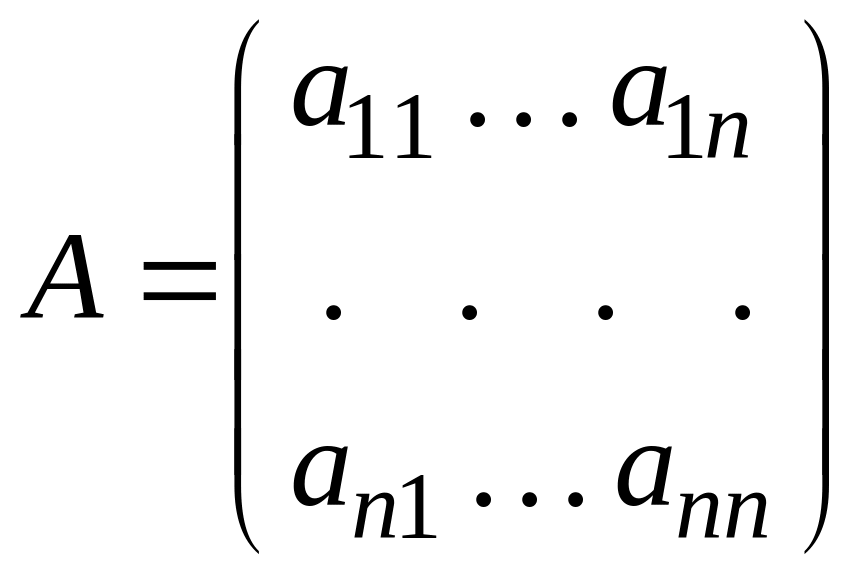 и
и
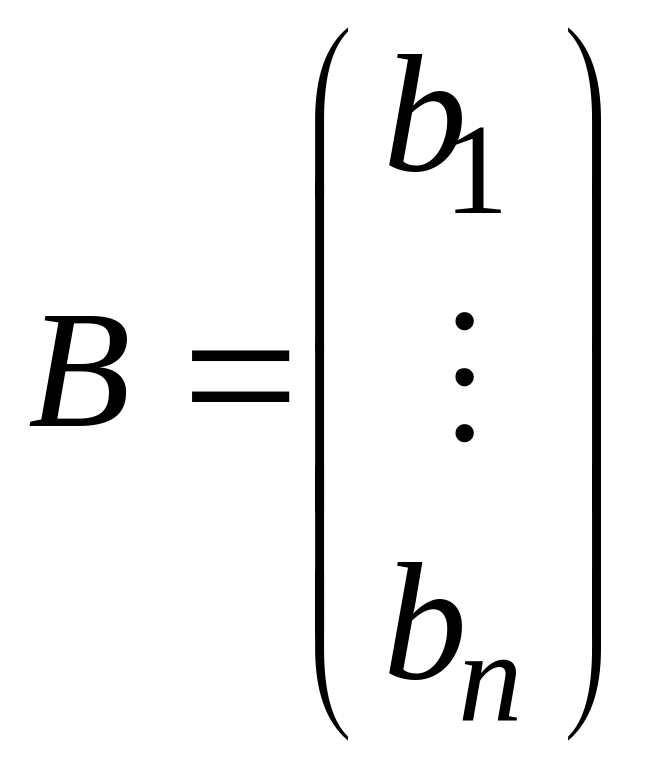 составлены из функций
составлены из функций
![]() а
а
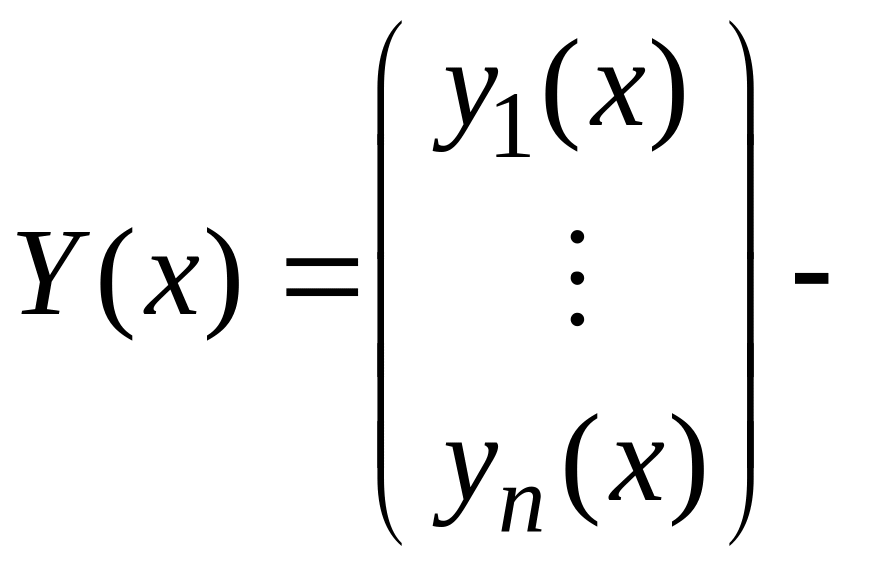 искомая вектор-функция.
искомая вектор-функция.
Введём в рассмотрение
оператор
дифференцирования
![]() Применение этого оператора к функции
будет обозначать её дифференцирование,
т.е.
Применение этого оператора к функции
будет обозначать её дифференцирование,
т.е.
![]() Произведение операторов – это оператор,
действие которого заключается в
последовательном применении этих
операторов к функциям. Следовательно,
Произведение операторов – это оператор,
действие которого заключается в
последовательном применении этих
операторов к функциям. Следовательно,
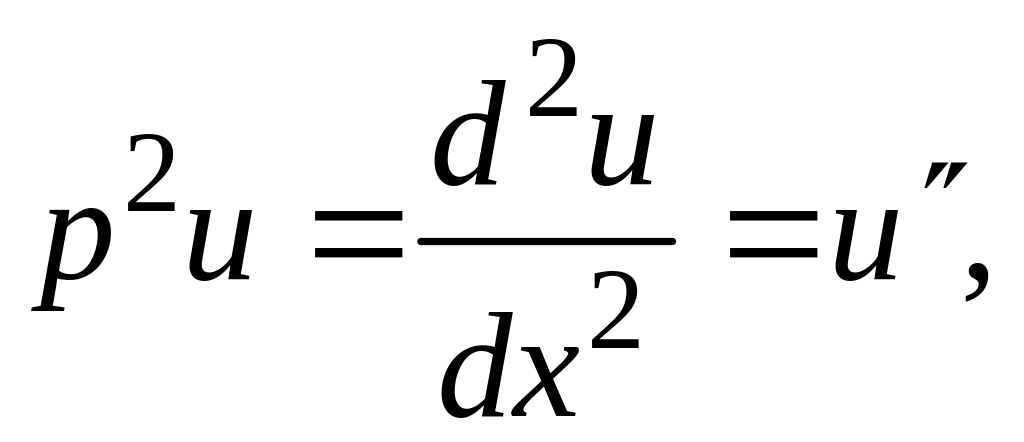
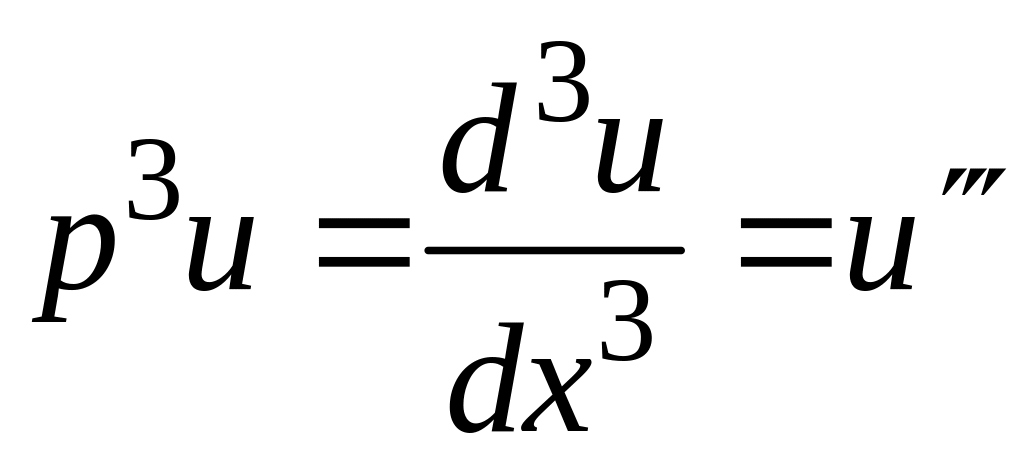 и т.д. Оператор
и т.д. Оператор
![]() является
линейным
в том
смысле, что
является
линейным
в том
смысле, что
![]() и
и
![]()
Если положить
![]() то уравнение (1) запишется короче:
то уравнение (1) запишется короче:
![]() (4)
(4)
Это уравнение называется линейным неоднородным, а уравнение
![]() (5)
(5)
линейным однородным. Аналогично этому система (3) – неоднородная, а система
![]() (6)
(6)
однородная. Заметим, что сумма двух решений однородного уравнения (или однородной системы) и вообще любая линейная комбинация решений также являются решениями уравнения (системы): действительно, если
![]() и
и
![]() то
то
![]()
Для систем доказательство аналогичное.
Если
![]() какое-либо решение неоднородной системы
(3), а
какое-либо решение неоднородной системы
(3), а
![]() решение однородной системы (6), то мы
имеем
решение однородной системы (6), то мы
имеем
![]() и
и
![]() Складывая эти два равенства, мы получим
Складывая эти два равенства, мы получим
![]() следовательно,
следовательно,
![]() является решением неоднородной системы.
Итак, сумма решения однородной системы
с решением неоднородной является
решением неоднородной. Пусть теперь
является решением неоднородной системы.
Итак, сумма решения однородной системы
с решением неоднородной является
решением неоднородной. Пусть теперь
![]() решения неоднородной системы. Тогда
решения неоднородной системы. Тогда
![]()
т.е.
![]() решение однородной системы. Так как
решение однородной системы. Так как
![]() то мы получим, что всякое решение
неоднородной системы получается из
другого решения этой системы прибавлением
к нему подходящего решения однородной
системы. Какое-либо фиксированное
решение однородной системы назовём
частным
решением.
Только что проведённые рассуждения
приводят к следующей теореме:
то мы получим, что всякое решение
неоднородной системы получается из
другого решения этой системы прибавлением
к нему подходящего решения однородной
системы. Какое-либо фиксированное
решение однородной системы назовём
частным
решением.
Только что проведённые рассуждения
приводят к следующей теореме:
Теорема 1.
Всякое
решение неоднородной системы
получается из какого-либо частного
решения этой системы прибавлением к
нему подходящего решения однородной
системы
![]()
Эту теорему можно записать символически следующим образом:
![]()
Таким образом, чтобы найти все решения неоднородной системы, достаточно найти какое-либо её решение (частное) и прибавить к нему все решения однородной системы.
Аналогичная теорема имеет место для линейных уравнений -го порядка. А именно:
Теорема 2.
Всякое
решение неоднородного уравнения
![]() является суммой какого-либо (частного)
решения этого уравнения и подходящего
решения однородного уравнения
является суммой какого-либо (частного)
решения этого уравнения и подходящего
решения однородного уравнения
![]()
Символическая запись этой теоремы имеет следующий вид:
![]()
§ 2. Фундаментальная система решений однородной системы и однородного уравнения
Пусть дана однородная
система
![]() где
где
![]() матрица, состоящая из непрерывных на
отрезке
функций
матрица, состоящая из непрерывных на
отрезке
функций
![]() Фундаментальной
системой решений
этой системы называется совокупность
вектор-функций
Фундаментальной
системой решений
этой системы называется совокупность
вектор-функций
![]() определённых на отрезке
и обладающих следующими свойствами: 1)
определённых на отрезке
и обладающих следующими свойствами: 1)
![]() линейно независимы; 2) всякое решение
линейно независимы; 2) всякое решение
![]() линейно выражается через
линейно выражается через
![]() т.е. представимо в виде
т.е. представимо в виде
![]() где
где
![]() постоянные.
постоянные.
Не случайно количество функций, входящих в фундаментальную систему решений, совпадает с количеством уравнений. Мы докажем, что система линейных уравнений первого порядка имеет фундаментальную систему решений, состоящую из функций.
Теорема 1.
Пусть дана
система
где
матрица размера
![]() состоящая из функций
состоящая из функций
![]() непрерывных на отрезке
непрерывных на отрезке
![]() Тогда существует фундаментальная
система решений
Тогда существует фундаментальная
система решений
![]() данной системы.
данной системы.
Доказательство.
Возьмём какие-нибудь
линейно независимых постоянных векторов
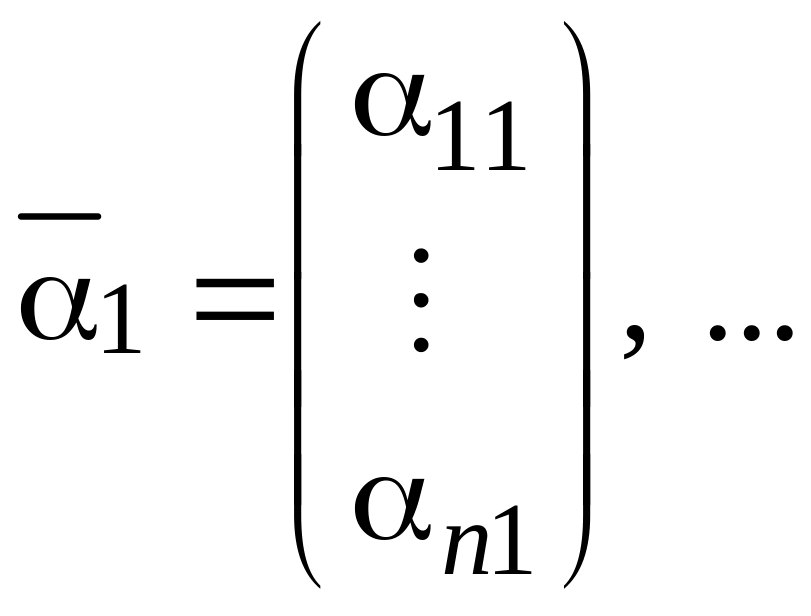
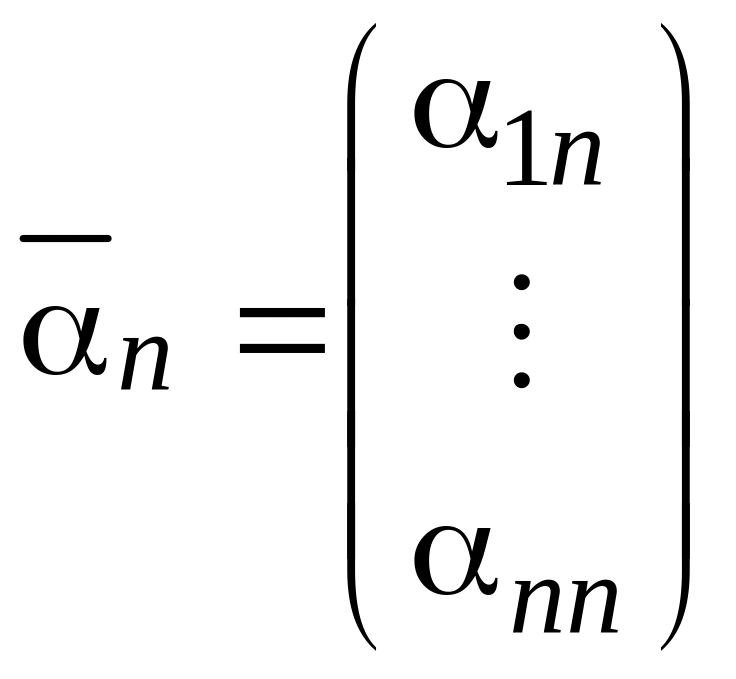 пространства
пространства
![]() например,
например,
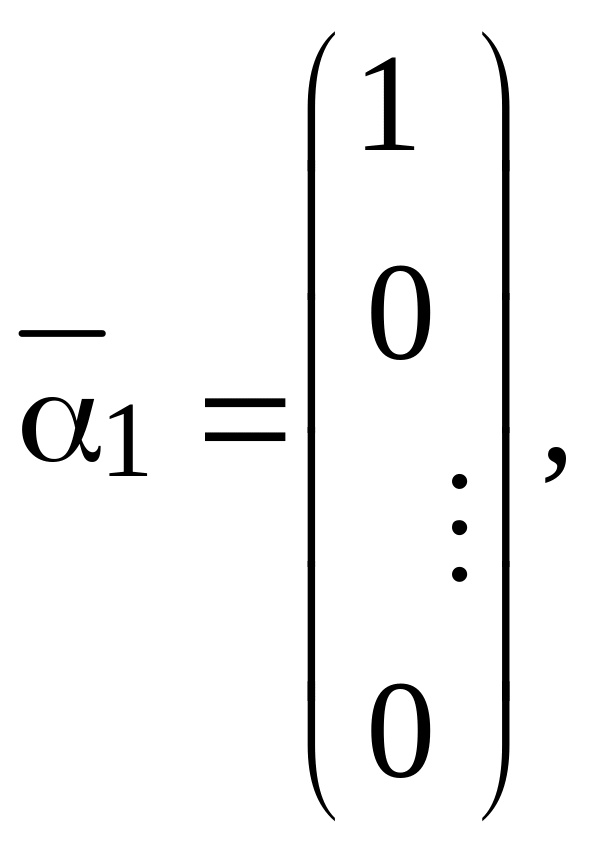
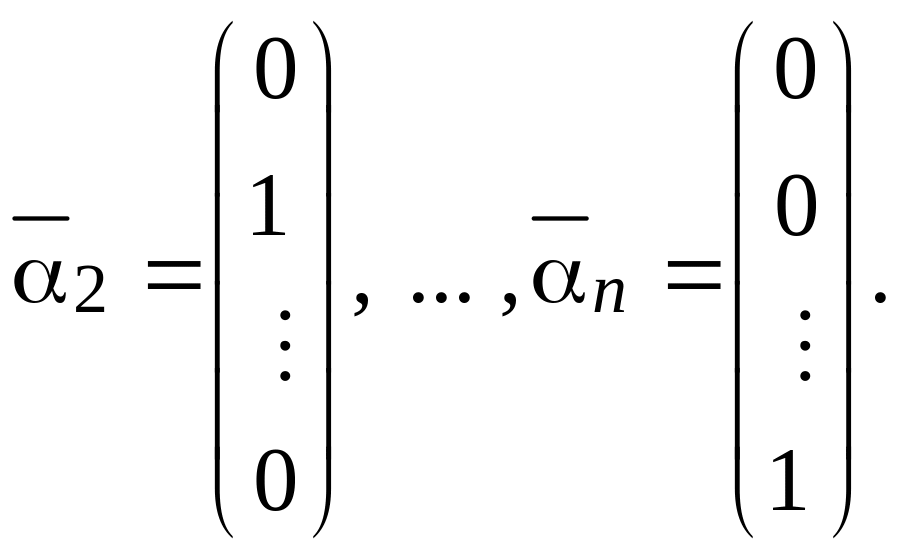 Пусть
Пусть
![]() точка отрезка
По теореме существования и единственности
решения системы можно найти такие
вектор-функцию
точка отрезка
По теореме существования и единственности
решения системы можно найти такие
вектор-функцию
![]() удовлетворяющих системе
и начальному условию
удовлетворяющих системе
и начальному условию
![]() Докажем, что
и есть фундаментальная система решений.
Докажем, что
и есть фундаментальная система решений.
Вначале докажем,
что функции
линейно независимы. Действительно,
пусть
![]() для некоторых
для некоторых
![]() Подставив в это тождество
Подставив в это тождество
![]() получим:
получим:
![]() т.е.
т.е.
![]()
Так как векторы
![]() линейно независимы, то
линейно независимы, то
![]() что и требовалось доказать.
что и требовалось доказать.
Теперь докажем,
что любое решение системы является
линейной комбинацией вектор-функций
![]() Пусть
Пусть
![]() любое решение системы. Тогда
любое решение системы. Тогда
![]() вектор из
вектор из
![]() Так как
Так как
![]() базис пространства
то
базис пространства
то
![]() для некоторых
для некоторых
![]() Положим
Положим
![]() Так как система дифференциальных
уравнений – линейная однородная и
функции
Так как система дифференциальных
уравнений – линейная однородная и
функции
![]() её решения, то функция
её решения, то функция
![]() как их линейная комбинация, также
является решением. Кроме того,
как их линейная комбинация, также
является решением. Кроме того,
![]()
Таким образом,
![]() и
и
![]() В виду единственности решения
В виду единственности решения
![]() Следовательно,
Следовательно,
![]()
Рассмотрим теперь линейное уравнение п-го порядка
![]() (7)
(7)
где
![]() функции, непрерывные на отрезке
Фундаментальной
системой решений
уравнения (7) называется совокупность
непрерывных на отрезке
функций
функции, непрерывные на отрезке
Фундаментальной
системой решений
уравнения (7) называется совокупность
непрерывных на отрезке
функций
![]() удовлетворяющих условиям:
удовлетворяющих условиям:
1)
![]() линейно независимые решения этого
уравнения;
линейно независимые решения этого
уравнения;
2) любое решение
![]() уравнения линейно выражается через
функции
уравнения линейно выражается через
функции
![]() т.е. представляется в виде
т.е. представляется в виде
![]() где
где
![]() постоянные числа.
постоянные числа.
Теорема 2. Всякое линейное однородное дифференциальное уравнение -го порядка имеет фундаментальную систему решений, состоящую из -линейно независимых функций решений этого уравнения.
Доказательство. Выведем эту теорему из теоремы 1, сведя уравнение -го порядка к системе. Очевидно, уравнение (7) равносильно системе дифференциальных уравнений первого порядка
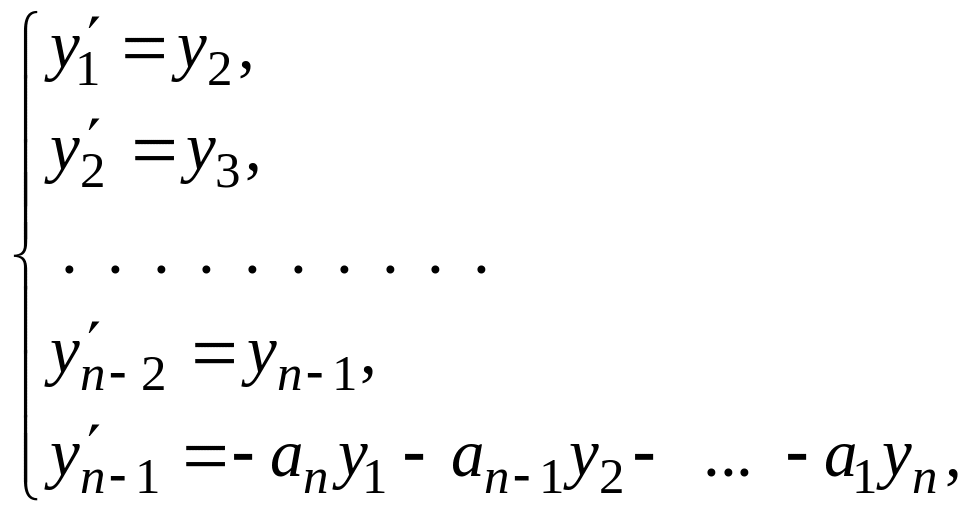 (8)
(8)
при этом
![]()
![]() По теореме 1 существует фундаментальная
система решений
системы (8). Из вида системы (8) следует,
что вектор-функции
По теореме 1 существует фундаментальная
система решений
системы (8). Из вида системы (8) следует,
что вектор-функции
![]() имеют вид
имеют вид
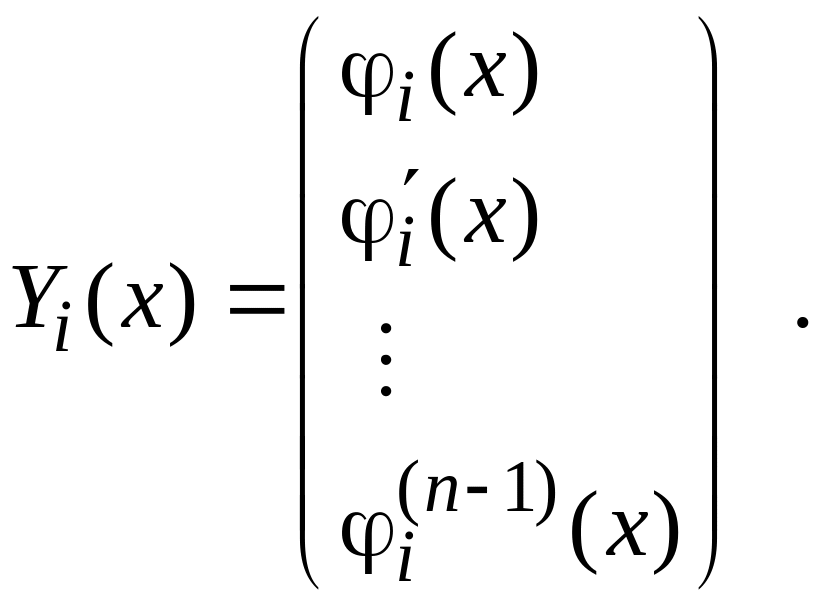 Проверим, что
и есть фундаментальная система решений
уравнения (7). Действительно, если
Проверим, что
и есть фундаментальная система решений
уравнения (7). Действительно, если
![]()
то, дифференцируя это равенство, будем получать
![]()
![]()
откуда следует
равенство
![]() Так как
линейно независимы, то
Так как
линейно независимы, то
![]() Если теперь
Если теперь
![]() любое решение уравнения (7), то
любое решение уравнения (7), то
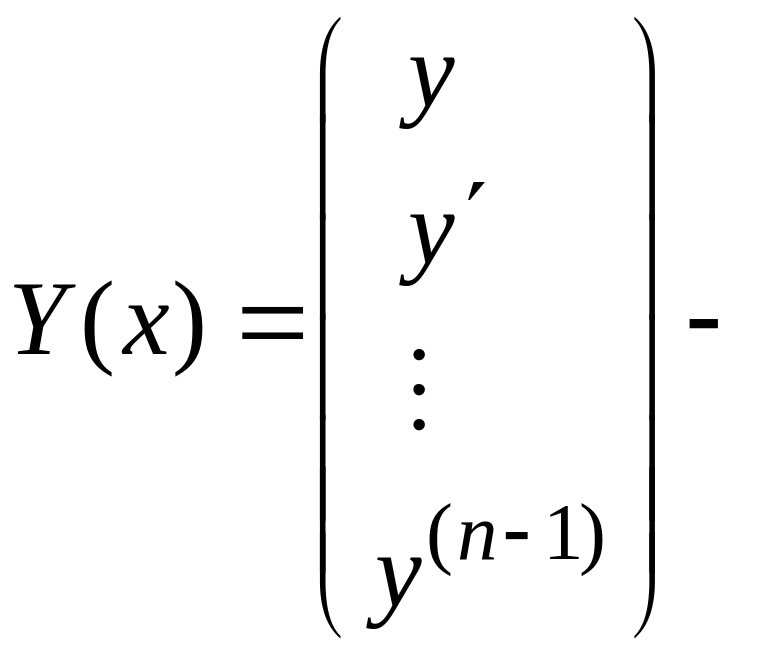 решение системы (8). Следовательно,
решение системы (8). Следовательно,
![]() для некоторых
для некоторых
![]() а значит,
а значит,
![]()
Замечание. Результаты этого параграфа показывают, что все решения линейной однородной системы дифференциальных уравнений первого порядка, а также все решения линейного однородного дифференциального уравнения -го порядка образуют линейное пространство над полем действительных чисел. Фундаментальная система решений – базис этого пространства.
