Разбор типовых примеров
Пример 1.
Решить уравнение методом вариации
постоянных:
Решение.
Сначала решим однородное уравнение
Его характеристическое уравнение имеет
вид
его корни:
Функции
и
образуют фундаментальную систему
решений однородного уравнения, а его
общее решение имеет вид
Решение неоднородного уравнения будем
искать в виде
Продифференцируем это равенство:
Потребуем, чтобы
(21)
Тогда
Отсюда
Подставим выражения
для
в исходное уравнение:
После
упрощения получаем:
Это равенство вместе с равенством (21)
составляют систему линейных уравнений
относительно
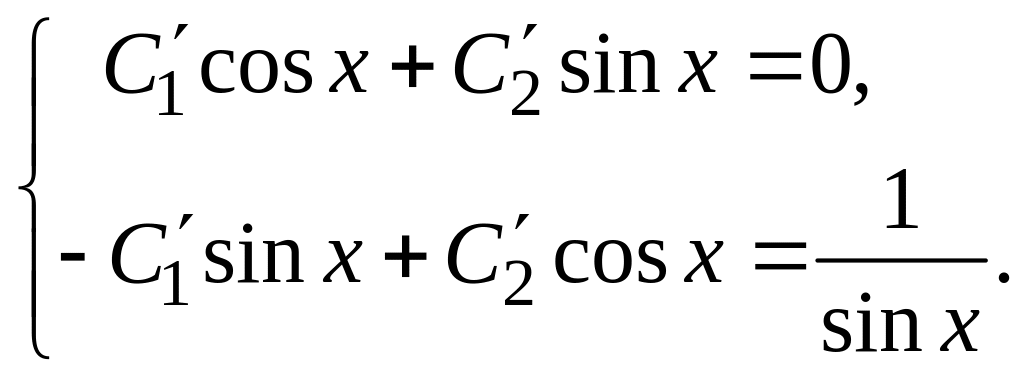
Решив эту систему,
получим:
Проинтегрировав эти равенства, получим:
где
постоянные. Следовательно, общее решение
уравнения имеет вид
Это окончательный ответ.
На примере данного
уравнения хорошо видно строение общего
решения неоднородного уравнения.
Действительно, перепишем последнюю
формулу в виде
Тогда мы увидим, что
частное решение неоднородного уравнения,
а
общее решение однородного.
Пример 2. Найти
общее решение
уравнения
.
Решение.
Найдем сначала общее решение
соответствующего однородного уравнения
.
Так как
,
то
,
,
.
Будем искать решение неоднородного
уравнения в виде
.
Неизвестные функции
и
определим из системы
;
;
.
;
.
;
.
.
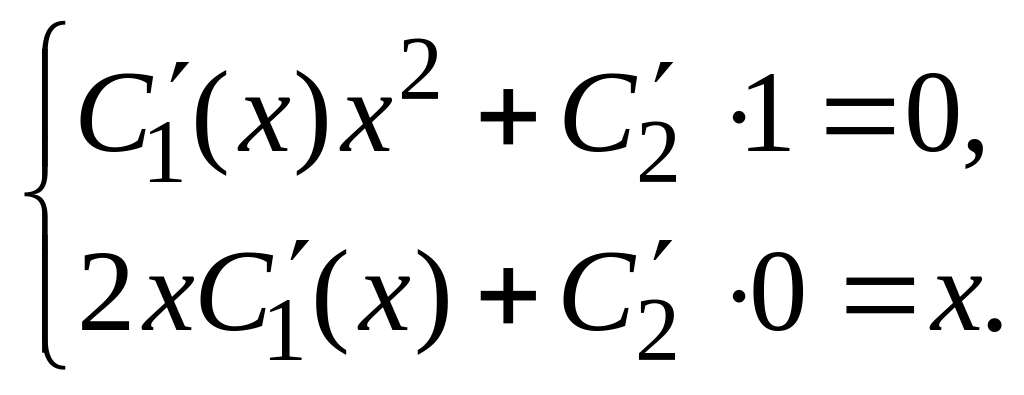
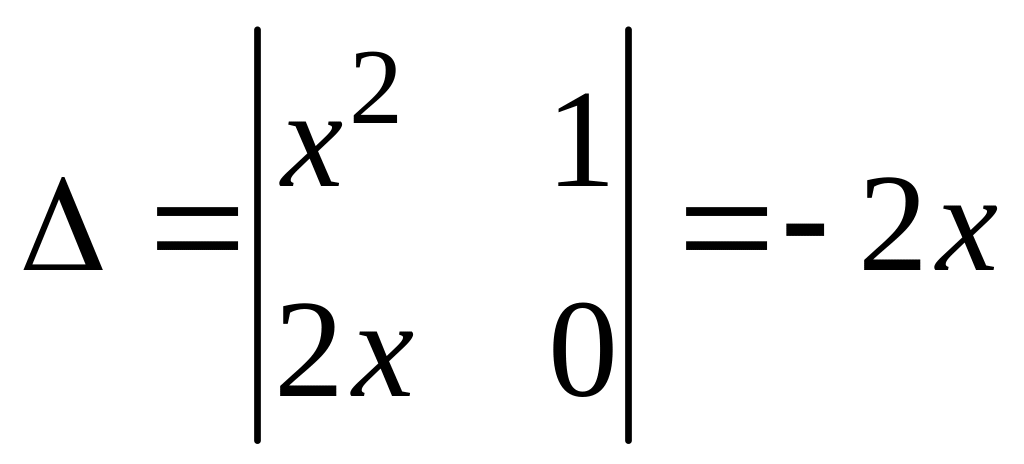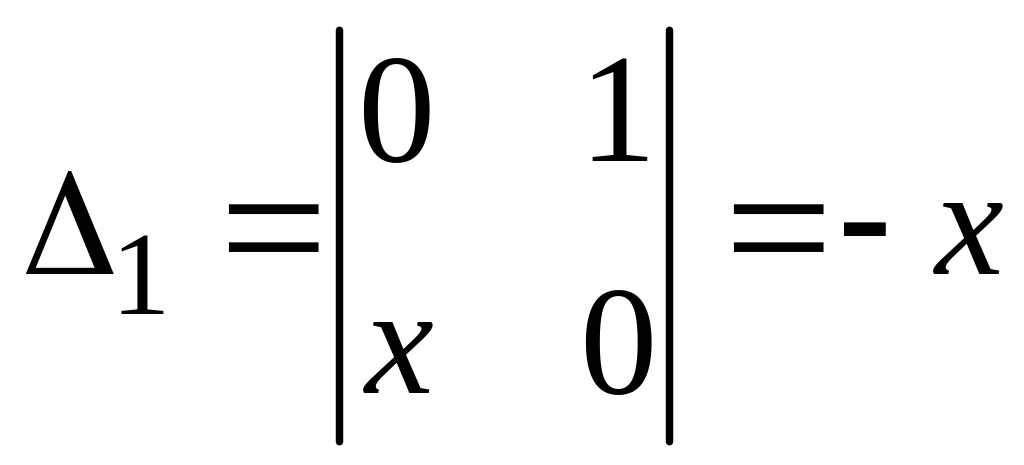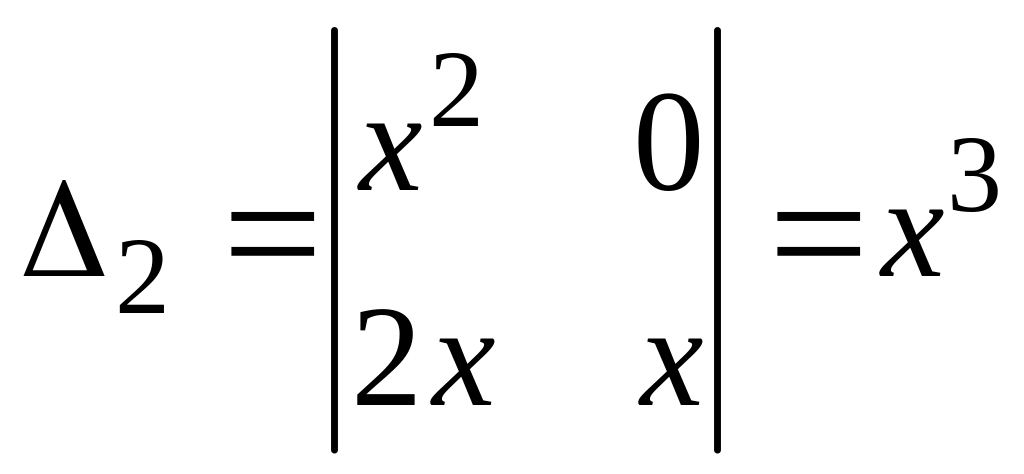Пример 3. Решить систему методом вариации постоянных:
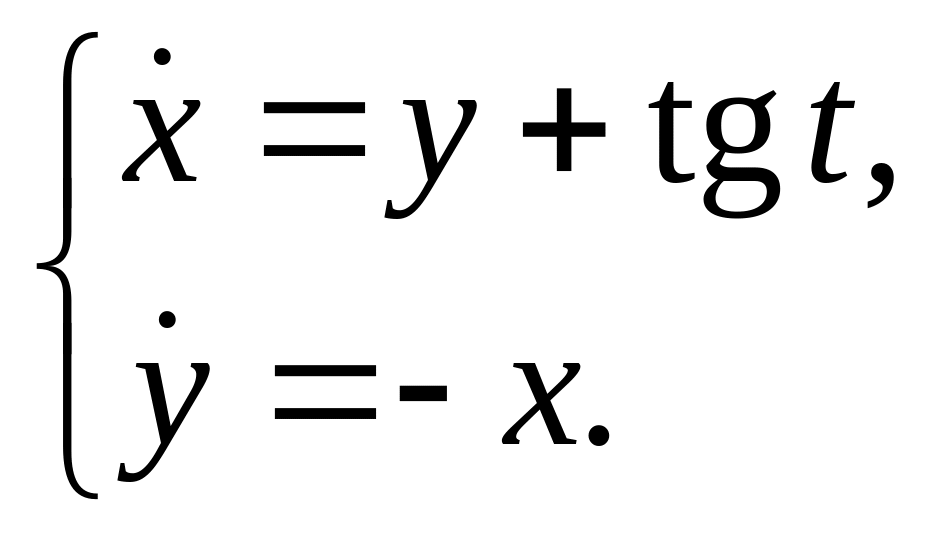
Решение.
Сначала решим однородную систему
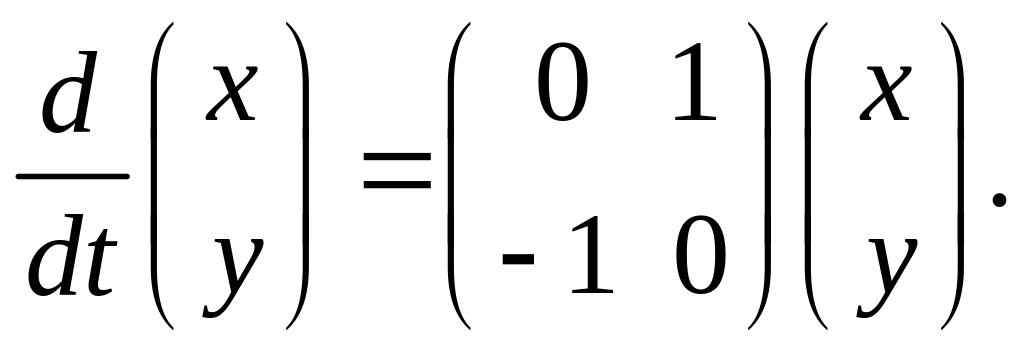Характеристическое уравнение
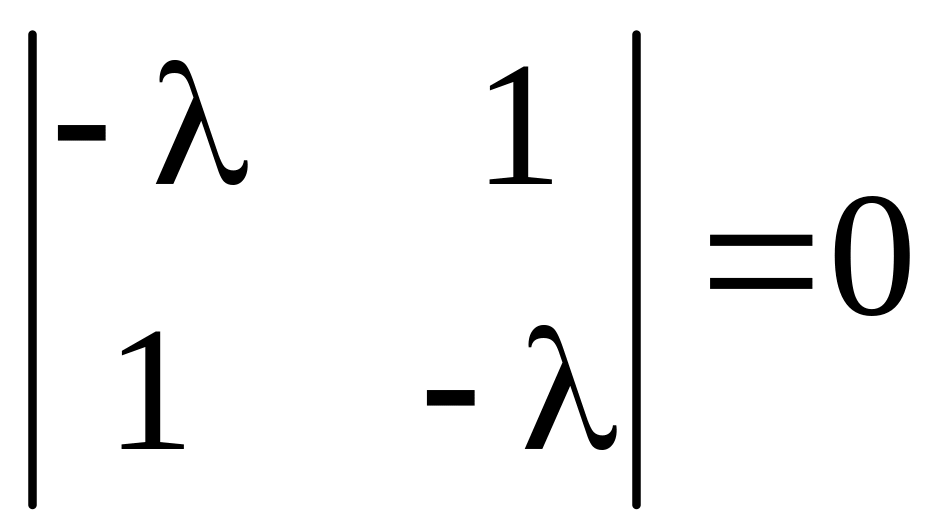имеет корни
Собственный вектор, соответствующий
равен
Поэтому
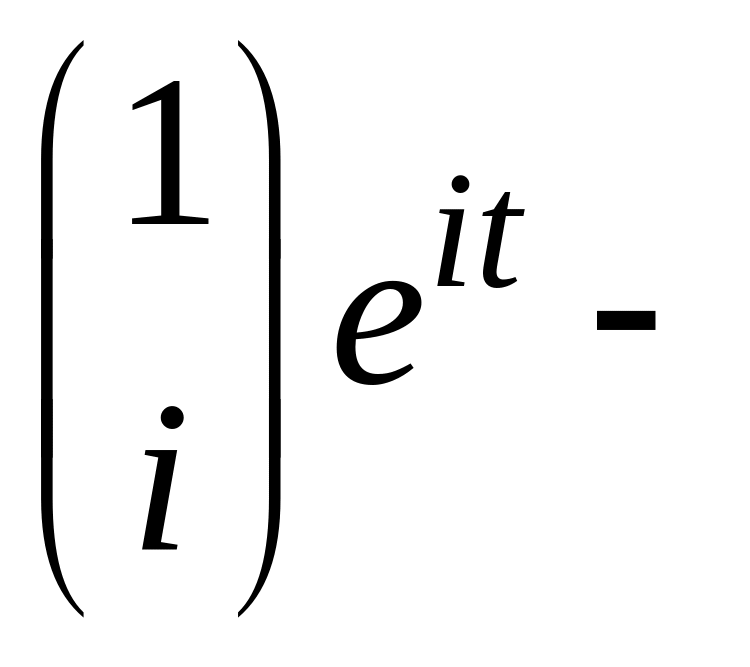комплексное решение системы. Выделим
действительную и мнимую части:
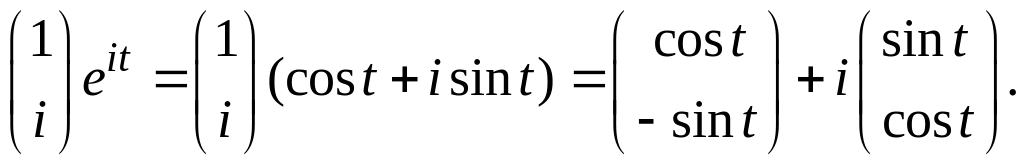
Значит, общее решение однородной системы имеет вид
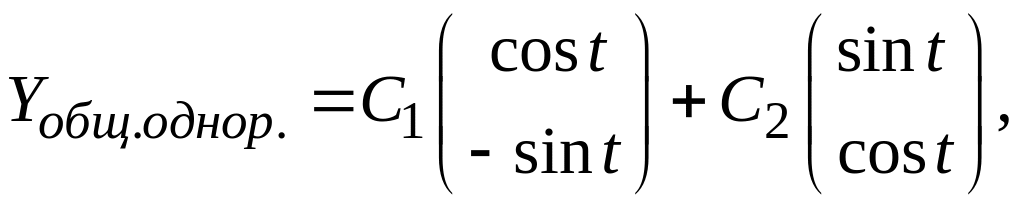где
постоянные.
Переходя к решению
неоднородной системы, будем далее
считать, что
Тогда
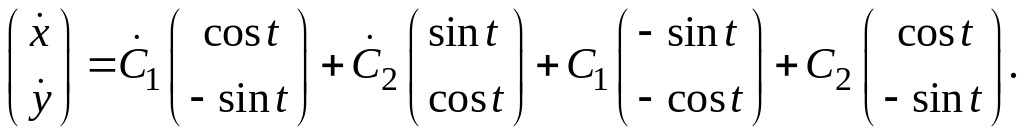
Подставив в исходную
систему, получим:
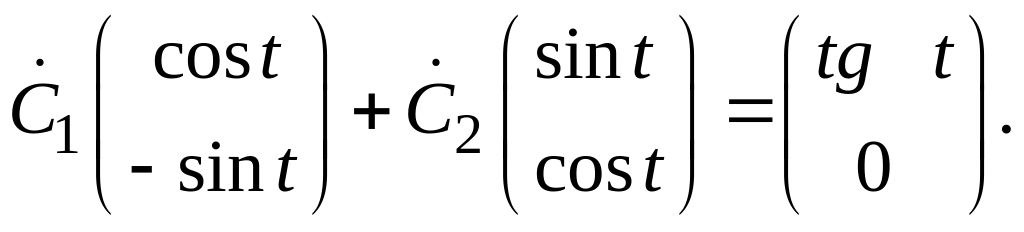Решив эту систему линейных алгебраических
уравнений относительно
получим:
Проинтегрировав эти равенства, будем
иметь
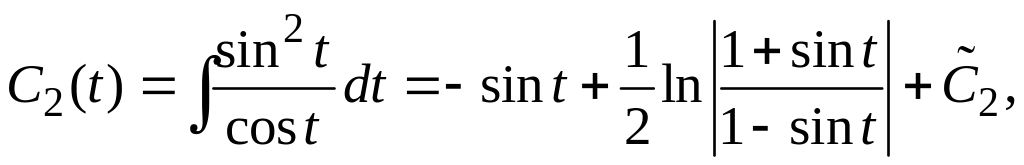где
постоянные. Таким образом, общее решение
исходной системы имеет вид
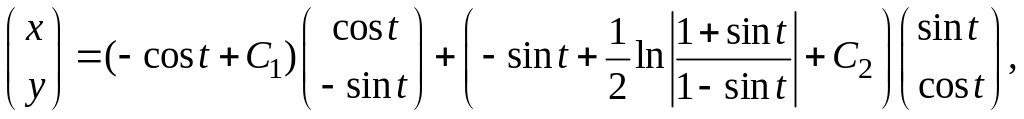
где постоянные.
Задачи для самостоятельного решения
Применяя метод вариации произвольных постоянных, проинтегрировать дифференциальные уравнения:
1. 
; 2. 
;
3. 
; 4. 
;
5. 
; 6. 
;
7. 
.
8. Решить
неоднородную систему методом вариации
постоянных
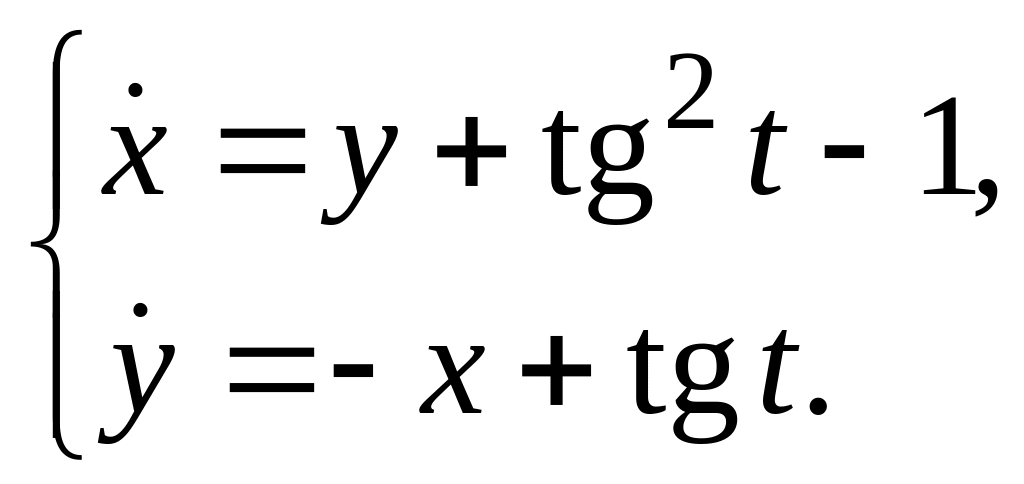
Ответы. 1. 
.
2. 
.
3. 
.
4. 
.
5. 
.
6. 
.
7. 
.
8. 
;
.