Интегрирование выражений вида .
Докажем,
что любой такой интеграл – берущийся
в элементарных функциях. Пусть
,
т.к.
.
Пусть m=НОК
,
.
Сделаем замену:
,
тогда
,
причем последнее выражение - рациональное,
т.к. m делится на любое
.
Тогда
получим, что x=φ(t), dx=φ΄(t)dt, где φ(t) и φ΄(t)dt
– рациональные выражения, поэтому:
- тоже рациональное выражение
Билет 33
Первая подстановка Эйлера (Леонарда)
Пусть
многочлен
имеет
вещественные корни.
Пусть
- корни, тогда
.
Рассмотрим
подстановку
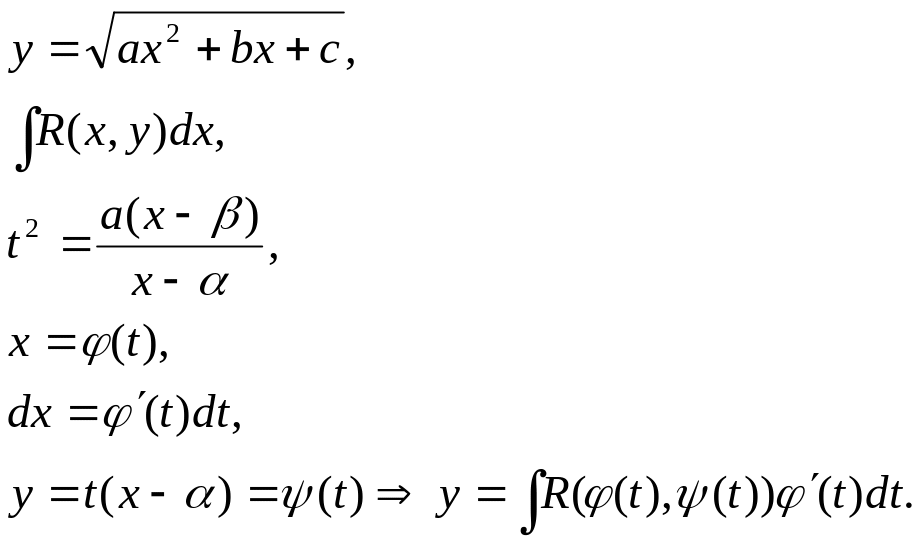
Билет 34
Вторая подстановка
Эйлера для
интегралов вида
,
где
.
Корни
трехчлена ax2+bx+c комплéксные. Тогда надо
считать, что a>0, иначе трехчлен был бы
отрицателен для всех x. Делаем
подстановку
.Возводя
это равенство в квадрат и заменяя
его выражением, получим:
Где x, y и dx – некоторые рациональные функции от t. В конечном счете получаем:
.
Билет 35
Интегрирование тригонометрических выражений.
Пусть
,
где
и
- многочлены от
и
.
1)
Если один из многочленов
,
четный по
,
а другой – нечетный по
,
то подстановка
рационализирует интеграл.
2)
Если один из многочленов
,
четный по
,
а другой – нечетный по
,
то подстановка
рационализирует интеграл.
3)
Если оба многочлена четные по
и
,
то подстановка
рационализирует интеграл.
3’)
Выражения вида
,
где
и
- четные. Они сходны с 3 случаем, где
4) Универсальная подстановка.
Рационализация
также достигается с помощью подстановки
,
которая называется универсальной.
В самом деле,
;
;
.
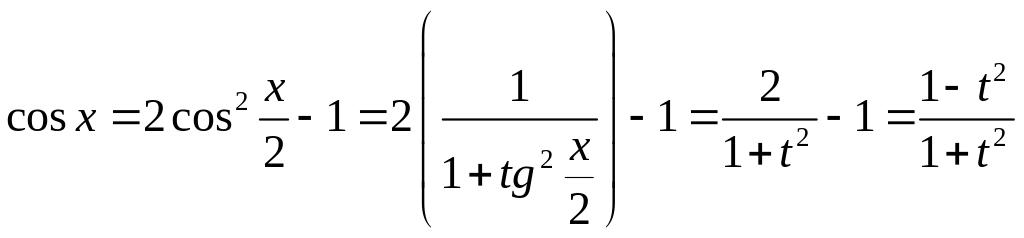5)
Выражения вида
;
;
.
Они рационализируются с помощью перевода
в тригонометрические суммы.
Билет 36
Тригонометрические подстановки.
Следующие интегралы превращаются в тригонометрические выражения при помощи тригонометрических подстановок:
Пример:
Билет 37
Определенный интеграл Римана. Эквивалентные определения. Условие Коши.
Пусть
задана функция f(x)
на отрезке
.
Составим разбиение R:
.
Это
интегральная сумма, соответствующая
разбиению R
и выбору точек
.
Если
существует предел при
интегральных
сумм
,
и он не зависит от R
и
,
то он называется определенным
интегралом Римана.
Определение по Коши:
По Гейне:
,
где
-
последовательность разбиений.
Критерий Коши:
Билет 38
Ограниченность интегрируемой функции.
Теорема:
Если
функция f(x)
интегрируема на [a,b]
и существует
,
то функция ограничена на этом отрезке.
Доказательство:
От
противного: пусть f(x)
неограниченна на [a,b].
Введем произвольное разбиение R:
.
Т.к. функция неограниченна на [a,b],
то она неограниченна хотя бы на одном
из отрезков
.
Пусть
-
номер того отрезка, на котором функция
неограниченна. Тогда рассмотрим
интегральную сумму:
-
т.е. выделили суммы одно слагаемое.
Обозначим
,
тогда получим:
(следует
из неравенства о модулях). Тогда возьмем
произвольное N
и сделаем разность
.
Для этого у нас должно быть
.
У нас функция неограниченна на отрезке
,
значит
.
Тогда интегральная сумма будет
,
т.е. будет являться величиной неограниченной,
т.е. не будет существовать ее предела,
а значит и
,
что противоречит условию.
Теорема доказана.
Билет 39