2.4.4. Метод моментів

Метод моментів ґрунтується на тому, що невідомі параметри теоретичного розподілу (розподілу генеральної сукупності) визначаються із рівнянь, які добуваються прирівнюванням важливіших числових характеристик (моментів) теоретичного розподілу відповідним числовим характеристикам емпіричного розподілу. Так, нехай заданий, наприклад, вид теоретичного розподілу , який визначається невідомим параметром . Для знаходження одного параметра необхідне одне рівняння відносно даного параметра. Для цього використовується момент 1-го порядку (математичне сподівання) теоретичного розподілу і відповідна числова характеристика емпіричного розподілу – вибіркове середнє. Знаходимо математичне сподівання як функцію від :

і функцію вибірки:

Порівнюючи їх, одержуємо рівняння для визначення оцінки невідомого параметра :

(2.28)

Для знаходження оцінок двох невідомих параметрів , звичайно беруть математичне сподівання і дисперсію теоретичного розподілу та відповідні їм числові характеристики емпіричного розподілу – вибіркове середнє і вибіркову дисперсію . Одержують два рівняння:

(2.29)

Розв’язуючи цю систему, знаходять відповідні оцінки .

Оцінки методу моментів звичайно є слушними, однак за ефективністю вони не є «найкращими». Тим не менш, метод моментів часто використовується на практиці, оскільки приводить до порівняно простих обчислень.

Приклад 2.2. Знаходження методом моментів оцінки невідомого параметра експоненціального розподілу.

Статистична модель. Генеральна сукупність має експоненціальний розподіл із щільністю розподілу , де – невідомий параметр. Вибіркові значення узяті із однієї і тієї ж генеральної сукупності. Знайдемо методом моментів оцінку невідомого параметра розподілу .

Розв’язання. Визначимо математичне сподівання експоненціального розподілу:

.

Далі по вибірці знаходимо вибіркове середнє емпіричного розподілу :

.

Із рівняння

знаходимо оцінку параметра :

Алгоритм у Mathсad

Початкові дані

Моделювання вибірки об’єму із генеральної сукупності розподіленої за експоненціальним законом з параметрам і одержання варіаційного ряду

Фрагмент вибірки

Середнє значення

m := mean(x) m = 0.103

Оцінка параметра

_◄

Приклад 2.3. Особливо зручне застосування методу моментів, коли шукані параметри розподілу самі є деякими числовими характеристиками. Знайдемо методом моментів оцінки невідомих параметрів a і нормального розподілу.

Статистична модель. Вибірка одержана із генеральної сукупності з нормальним розподілом із щільністю розподілу:

,

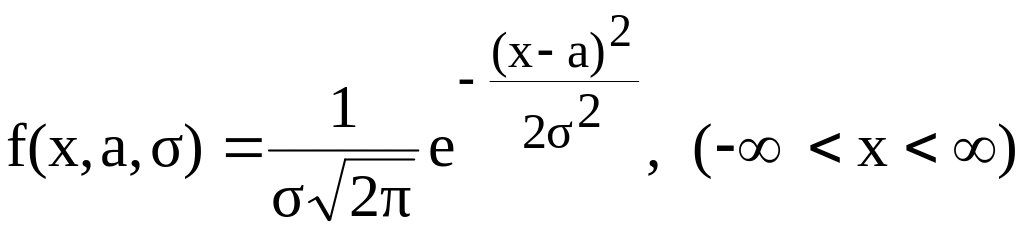де a і – невідомі параметри розподілу.

Знайдемо методом моментів оцінки невідомих параметрів a і .

Розв’язання. Визначимо математичне сподівання і дисперсію розподілу:

,

За даними вибірки знаходимо вибіркові числові характеристики і прирівнюємо їх до відповідних числових характеристик теоретичного розподілу:

У результаті одержуємо шукані оцінки параметрів:

Алгоритм у Mathсad

Початкові дані

Моделювання вибірки об’єму із генеральної сукупності розподіленої за нормальним законом з параметрами і одержання варіаційного ряду

Фрагмент вибірки

Середнє арифметичне і середнє квадратичне

_{Оцінки параметрів розподілу}

_◄