2.5.7. Оцінка ймовірності біноміального розподілу за частотою

Статистична модель. Нехай проводяться незалежні спостереження з невідомою ймовірністю появи події у кожному випробуванні. Необхідно оцінити невідому ймовірність по частоті, тобто знайти її оцінку і надійний інтервал.

За точкову оцінку ймовірності приймають частоту

(2.74)

де кількість появ події А, кількість випробувань.

Ця оцінка незсунена, тобто її математичне сподівання дорівнює ймовірності р. Дійсно, враховуючи, що одержимо

Якщо об’єм вибірки достатньо великий (практично при ) і ймовірність (частка ознаки) не дуже мала (так що при ), то для оцінки ймовірності може бути застосована асимптотична формула Лапласа. При цих умовах біноміальний розподіл добре апроксимується нормальним розподілом з параметрами

Використовуючи формулу ймовірності заданого відхилення нормальної випадкової величини від свого середнього значення, одержимо:

.

Для знаходження надійного інтервалу , який накриває оцінюваний параметр з надійністю , потрібно, щоб виконувалась умова:

, (2.75)

де – . Звідси знаходимо граничну похибку :

(2.76)

Таким чином, з імовірністю виконується нерівність:

.

Обидві частини нерівності додатні. Тому підвівши їх до квадрату, одержимо рівносильну нерівність

,

розв’язуючи яку відносно , одержимо границі надійного інтервалу:

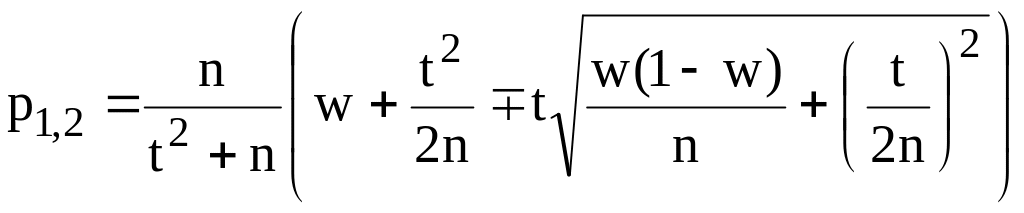(2.77)

Таким чином, надійний інтервал знайдений.

При великих значеннях доданки і дуже малі і множник . Тому вираз у дужках буде дорівнювати

. (2.78)

Отже, надійний інтервал для ймовірності біноміального розподілу (генеральної частки) при великому буде дорівнювати:

. (2.79)

Для безповторної вибірки середнє квадратичне треба замінити на

, (2.80)

де – об’єм генеральної сукупності. Тоді буде дорівнювати:

. (2.81)

Приклад 2.9. Проведені незалежні випробування з однаковою, але невідомою ймовірністю р появи події А у кожному випробуванні. Знайдемо надійний інтервал для оцінки ймовірності р біноміального розподілу з надійністю якщо у 80 випробуваннях подія А відбулась 16 разів.

Алгоритм у Mathcad

_{Вхідні дані задачі}

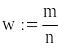
_{Квантиль нормованого нормального розподілу}

_{Границі надійного інтервалу}

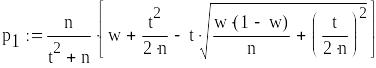
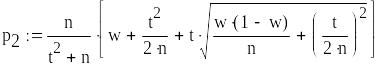
_{Надійний інтервал для імовірності появи події у схемі незалежних випробувань}

_◄

8. Оцінка математичного сподівання

експоненціального розподілу

Статистична модель. Вибірка об’єму одержана із генеральної сукупності, розподіленої за експоненціальним законом з параметром Припускається, що параметр невідомий. Треба визначити надійний інтервал для математичного сподівання цього розподілу.

Математичне сподівання і дисперсія генеральної сукупності відповідно дорівнюють

.

Для цього розподілу звичайно оцінюється не параметр , а обернена до нього величина , тобто математичне сподівання експоненціального розподілу

Побудова надійного інтервалу базується на тому, що випадкова величина , де – вибіркові значення, які мають експоненціальний розподіл з параметром , не залежить для математичного сподівання від і має розподіл з 2n ступенями свободи.

Алгоритм побудови надійного інтервалу

1. Обчислюється точкова оцінка середнього арифметичного

2. Задається рівень значущості і визначаються квантилі розподілу відповідних порядків і , де – функція, обернена до функції розподілу з 2n ступенями свободи. У квантилі обчислюються за функцією qchisq( ).

4. Обчислюються границі надійного інтервалу

.

Приклад 2.10. Вибірка об’єму одержана із генеральної сукупності, розподіленої за експоненціальним законом з невідомим параметром Вважаючи, що точне значення невідоме, при рівні значущості визначимо надійний інтервал для параметра і математичного сподівання досліджуваної генеральної сукупності.

Розв’язання. Змоделюємо вибірку об’єму у припущенні, що генеральна сукупність розподілена за експоненціальним законом з параметром Вибірку моделюємо за допомогою функції . Знаходячи квантилі – розподілу і визначаючи точності оцінок для параметра і параметра , знаходимо відповідні надійні інтервали.

_{Алгоритм у Mathcad}

_{Моделюємо вибірку}

_{Фрагмент вибірки}

Точкова оцінка математичного сподівання

_{Рівень значущості і кількість ступенів свободи}

Квантилі – розподілу

Границі надійного інтервалу для математичного сподівання

Надійний інтервал для математичного сподівання

Границі надійного інтервалу для параметра

Надійний інтервал для параметра

_◄