Алгоритм у Mathcad

Початкові дані

Моделювання вибірки об’єму із генеральної сукупності розподіленої за нормальним законом з параметрами і одержання варіаційного ряду

_{Фрагмент варіаційного ряду}

Визначення розмаху вибірки

Задання кількості інтервалів групування і визначення довжини інтервалів групування

_{Визначення масиву границь інтервалів групування}

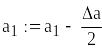
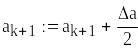
_{Визначення масиву частотного розподілу варіаційного ряду}

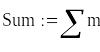
_{Числові характеристики: середнє арифметичне, дисперсія, середнє квадратичне відхилення емпіричного розподілу}

Медіана

Модальний інтервал ( номер модального інтервалу) і мода

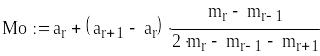
_{Коефіцієнт асиметрії}

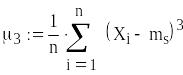
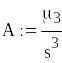
Ексцес

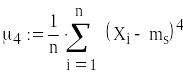
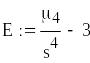
Щільність нормального розподілу з параметрами

Середини інтервалів

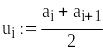
Емпірична функція розподілу

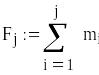
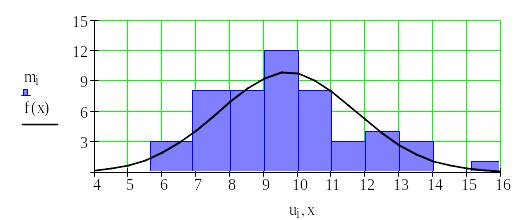
Рис.2.1. Гістограма частот і графік щільності нормального розподілу

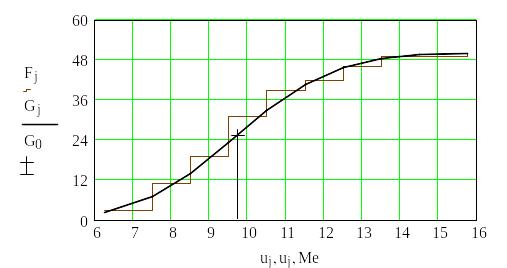
Рис. 2.2. Графіки емпіричної і теоретичної функцій розподілу F i G

і значення функції розподілу у точці (відмічено знаком +).

Теоретична функція розподілу з параметрами

_{Значення теоретичної функції розподілу у точці Ме}

◄

2.4. Статистичні оцінки параметрів розподілів

2.4.1. Поняття статистичної оцінки параметрів

Задача статистичного оцінювання параметрів розподілів полягає у тому, щоб за результатами вибірки оцінити як можна точніше значення характеристик генеральної сукупності, наприклад, середнього значення, дисперсії, частоти тощо.

Припустимо, що розподіл ознаки Х (генеральної сукупності) належить до відомого класу розподілів, який залежить від одного або декількох невідомих параметрів і задається функцією ймовірностей (для дискретної випадкової величини Х) або щільністю ймовірностей (для неперервної випадкової величини Х). Наприклад, це параметр для розподілу Пуассона або параметри і для нормального розподілу. У цьому випадку визначення невідомого розподілу зводиться до знаходження оцінок невідомих параметрів за вибіркою . Тут вибіркові значення можна розглядати як числа , якщо експеримент проведено і вибірка відбулась, і як n незалежних випадкових величин або n екземплярів випадкової величини до експерименту. Випадкові величини мають одну і ту ж функцію розподілу і закон розподілу будь-якої статистики однозначно визначається цією функцією, зокрема, невідомим параметром .

 Оцінкою параметра називається будь-яка величина, яка є випадковою функцією вибірки , так звана статистика, за значенням якої можна судити про значення параметра .

Отже, оскільки – випадкові величини, то і оцінка (на відміну від оцінюваного параметра – величини невипадкової, детермінованої) є випадковою величиною, яка залежить від закону розподілу випадкової величини Х і числа n.

Завжди існує множина функцій від результатів спостережень (від n екземплярів випадкової величини X), які можна прийняти за оцінку параметра . Наприклад, якщо параметр є математичне сподівання випадкової величини X, тобто генеральне середнє a, то за оцінку можна прийняти середнє арифметичне результатів спостережень – вибіркову середню .

Статистику треба підібрати так, щоб вона по можливості більш точно оцінювала невідомий параметр . Для цього вона повинна мати такі властивості як незсуненість, слушність і ефективність.

 Оцінка параметра називається незсуненою, якщо її математичне сподівання дорівнює оцінюваному параметру :

. (2.21)

У протилежному разі оцінка називається зсуненою.

Якщо ця рівність не виконується, то оцінка , одержана за результатами різних вибірок, буде у середньому або завищувати значення (якщо ), або занижувати його (якщо ). Таким чином, вимога незсуненності гарантує відсутність систематичних похибок при оцінюванні параметрів.

Якщо оцінка зсунена, то обчисливши її математичне сподівання і ввівши поправку, можна одержати незсунену оцінку.

Відзначимо, що усі вибіркові початкові моменти випадкової величини, включаючи вибіркове середнє, є незсуненими оцінками відповідних моментів розподілу генеральної сукупності. Однак вибіркова дисперсія є зсуненою (як і інші центральні вибіркові моменти). Далі буде показано, що:

. (2.22)

 Оцінка параметра називається слушною, якщо вона задовольняє закон великих чисел, тобто збігається за імовірністю до оцінюваного параметра:

(2.23)

Або, як кажуть, прямує до за імовірністю:

Якщо оцінка слушна, то практично вірогідно, що при достатньо великому n . Якщо оцінка є незсуненою, а її дисперсія при , то вона є слушною.

Умовам незсуненності і слушності можуть задовольняти декілька різних оцінок одного і того ж параметра. Тоді кращою з них буде та, яка має найменшу дисперсію:

. (2.24)

 Оцінка , яка має найменшу дисперсію, називається ефективною.

Якщо властивість незсуненності дає кращу оцінку, то властивість ефективності підвищує її точність. Це обумовлено тим, що від величини дисперсії оцінки безпосередньо залежить надійний інтервал, ширина якого пропорційна дисперсії. Таким чином, ефективність оцінки забезпечує найменший розкид можливих значень оцінки навколо істинного значення параметра .

Ефективність оцінок сильно залежить від розподілу генеральної сукупності. Так, якщо генеральна сукупність має нормальний розподіл, то вибіркове середнє і дисперсія будуть ефективними оцінками. Звичайно ефективна оцінка добувається на основі метода максимальної правдоподібності, у якому функція правдоподібності визначається, виходячи із припущення, що відомий клас розподілів, якому належить розподіл даної генеральної сукупності.

Нехай – незалежна вибірка, у якій кожне має щільність розподілу де невідомий параметр, а змінна щільності розподілу. Тоді при виконанні деяких умов регулярності має місце нерівність Крамера-Рао:

де незсунена оцінка параметра

Нерівність Крамера-Рао дає нижню границю для дисперсії незміщеної оцінки. Якщо для оцінки у цій нерівності досягається рівність, то ця оцінка буде ефективною.

 Ефективністю незміщеної оцінки називається величина

Із нерівності Крамера-Рао випливає, що Оцінка ефективна, якщо

Якщо оцінка параметра асимптотично нормальна з параметрами при то асимптотична ефективність визначається величиною Оцінка асимптотично ефективна, якщо