2.3. Числові характеристики статистичних розподілів

Статистичний розподіл вміщує повну інформацію про варіацію ознаки. Однак велика кількість числових даних, за допомогою яких він задається, ускладнює їх використання. Між тим, при розв’язанні багатьох задач ця інформація виявляється надмірною і може бути з успіхом замінена невеликою кількістю звідних характеристик розподілу.

Більш того, мистецтво статистичного аналізу якраз і визначається не безпосереднім використанням статистичного розподілу, а тим, наскільки успішно і повно вдається здійснити такий аналіз, спираючись на мінімальну кількість показників.

Для опису статистичних розподілів використовуються три види характеристик (показників):

● середні або характеристики центральної тенденції;

● характеристики мінливості варіант;

● характеристики, які відображають додаткові особливості розподілів, зокрема їх форму.

Усі вони обчислюються за результатами спостережень і побудованих у результаті їх первинної обробки статистичних розподілів. Тому їх називають статистичними. Розрахунок статистичних характеристик є другий після групування етап обробки даних спостережень. Цим, звичайно, не вичерпується статистичний аналіз, основною метою якого є встановлення загальних закономірностей змін ознаки. Однак, такий аналіз опирається на побудову теоретико-ймовірнісної моделі і буде розглядатись у подальшому після підготовки необхідного математичного апарату.

2.3.1. Середні величини

Кожній числовій характеристиці випадкової величини відповідає її статистична аналогія. Статистичні (вибіркові) числові характеристики є випадковими функціями вибіркових значень.

Середня величина характеризує типовий для сукупності розмір ознаки або, як іноді говорять, центральну тенденцію у розподілі. Очевидно практичне використання такої характеристики доцільне у тому випадку, коли окремі варіанти ряду розподілу концентруються поблизу деякого значення. Якщо ж сукупність дуже неоднорідна, результати спостережень значно відрізняються один від одного і не виявляють загальної тенденції, її використання стає чисто формальним.

Існують різні форми середніх. До вибору форми середнього слід підходити керуючись задачею дослідження і визначальною властивістю розподілу, яка повинна бути виражена цією характеристикою.

Основним видом середніх є середнє арифметичнє.

 Середнім арифметичним варіаційного ряду називається величина, яка обчислюється на основі вибіркових даних за формулами

Для незгрупованого ряду	Для згрупованого ряду	(2.5)

де – варіанти дискретного варіаційного ряду або середини інтервалів інтервального варіаційного ряду, – частоти, – відносні частоти,

.

Важливіша властивість середнього арифметичного – сума відхилень варіант від середнього значення дорівнює 0:

.

При розв’язанні практичних задач можуть застосовуватись і інші форми середньої – середнє геометричне і середнє гармонічне.

 Емпіричним середнім геометричним називається величина, яка обчислюється на основі вибіркових даних (для ознак з додатними можливими значеннями) за формулою:

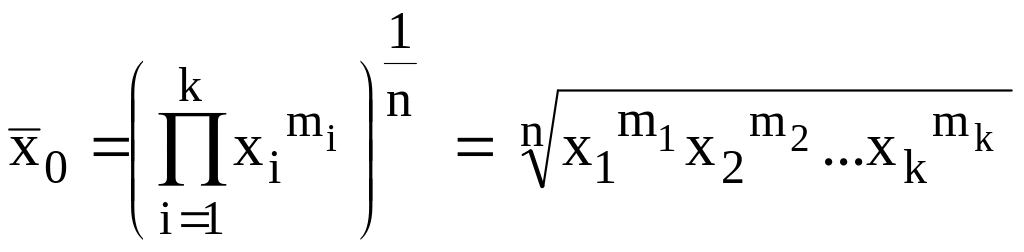(2.6)

Середнє геометричне знаходить застосування при розрахунках темпів зміни величин, зокрема, у тих випадках, коли мають справу з величиною, зміни якої відбуваються приблизно у прямо пропорційній залежності з досягнутим до цього моменту рівнем самої величини, наприклад, рівня доходу, або ж коли мають справу із середньою з відношень, наприклад, при розрахунках індексів цін.

 Емпіричним середнім гармонічним називається величина, яка обчислюється на основі вибіркових даних за формулою:

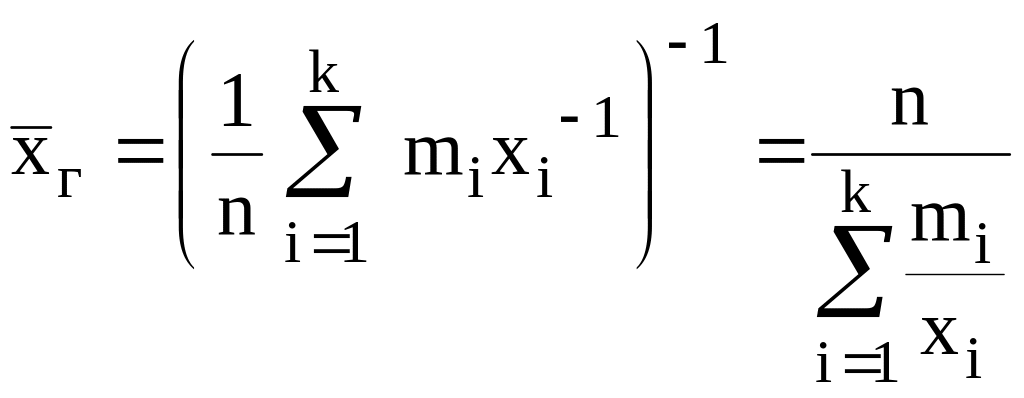(2.7)

Гармонічне середнє значення ряду чисел завжди менше середнього геометричного значення тих же чисел, а тим більше – їх середнього арифметичного. Область його застосування досить обмежена. У економіці, зокрема, користуються іноді середнім гармонічним при аналізі середніх норм часу, а також у деяких видах індексних розрахунків.

Окрім розглянутих середніх, які називаються аналітичними у статистичному аналізі, застосовують структурні або порядкові середні. Із них найбільш широко застосовуються медіана і мода.

 Медіаною Ме варіаційного ряду називається значення ознаки, яке розділяє ранжовану сукупність на дві рівні за чисельністю групи: перша містить варіанти із значеннями меншими Me, друга – із значеннями варіант більшими Me.

Із означення емпіричної функції розподілу (накопиченої частоти) випливає, що:

. (2.8)

Для дискретного варіаційного ряду з непарним числом членів медіана дорівнює середньому члену, а для ряду з парним числом членів – півсумі двох середніх членів.

Для інтервального варіаційного ряду знаходиться медіанний інтервал із умови . Значення медіани на цьому інтервалі знаходиться за допомогою інтерполяційної формули:

, (2.9)

де – накопичена частота, менша n/2, – наступна накопичена частота, більша або рівна n/2.

Зазначимо, що медіана може бути приблизно визначена за допомогою емпіричної функції розподілу або кумуляти як значення варіанти Me, для якої Це зручно зробити графічно.

 Модою Mo варіаційного ряду називається значення варіанти, якій відповідає найбільша частота.

У багатьох випадках мода є найбільш характерною для ряду розподілу і навколо неї концентрується більша частина варіант. При зміні крайніх членів ряду мода не змінюється, тобто вона має певну сталість до варіації ознаки. Тому її особливо зручно застосовувати при дослідженні рядів з невизначеними границями. Моду доцільно застосовувати також і в тому випадку, коли при вивченні варіації ознаки важко визначити одну превалюючу над усіма іншими частоту.

Для дискретного варіаційного ряду мода знаходиться безпосередньо за визначенням.

Для інтервального варіаційного ряду визначається модальний інтервал , якому відповідає найбільша щільність відносної частоти. Величина моди всередині модального інтервалу визначається за ітерполяційною формулою

, (2.10)

де , , – частоти відповідно модального, попереднього до модального і наступного за модальним інтервалів. У цій формулі замість частот можна використовувати частки.

Якщо визначений модальний інтервал, то реалізація такої формули не викликає труднощів.

Для строго симетричного розподілу, у якого частоти варіант, які рівновіддалені від моди, рівні, значення середньої арифметичної, медіани і моди співпадають, тобто . При порушенні симетрії ці три показника розходяться. Але якщо порушення симетрії не дуже сильно виражене, то між вказаними трьома видами середньої буде виконуватись наближена рівність

. (2.11)

На гістограмі розподілу мода визначається таким чином. Знаходиться прямокутник з найбільшою частотою (відносною частотою). З’єднуючи відрізками прямих вершини цього прямокутника з відповідними вершинами двох сусідніх прямокутників, одержують точку перетину цих відрізків (діагоналей), абсциса якої і буде модою варіаційного ряду.