2.5.3. Надійний інтервал для математичного сподівання нормального розподілу a при невідомому σ

Статистична модель. Випадкова величина X розподілена нормально. Необхідно знайти надійний інтервал для невідомого математичного сподівання a при невідомому середньому квадратичному відхиленні .

Визначимо за даними вибірки об’єму n із генеральної сукупності X вибіркове середнє і виправлену випадкову дисперсію (незсунену оцінку для ):

Випадкова величина розподілена нормально з параметрами a і .

Оскільки величина невідома, при побудові надійного інтервалу для a не можна користуватись нормальністю розподілу . У цьому випадку розглянемо статистику

. (2.47)

Доведено, що випадкова величина розподілена за законом Стьюдента з ступенями свободи, який не залежить від розподілу .

Нехай задана надійність оцінки . Знайдемо таке число , щоб виконувалась рівність

.

Замінивши нерівність у дужках рівносильною їй подвійною нерівністю, одержимо

(2.48)

Величину знаходимо за функцією , яка визначає квантиль розподілу Стьюдента.

Підставляючи знайдене значення у нерівність (2.48), одержимо надійний інтервал

(2.49)

який накриває невідомий параметр з надійністю γ.

Алгоритм побудови надійного інтервалу

1. Обчислюються точкові оцінки математичного сподівання і середнього квадратичного відхилення .

2. Задається надійна ймовірність або рівень значущості

3. Із рівняння , де – функція розподілу Стьюдента з ступенями свободи, обчислюється квантиль де функція, обернена до функції .

4. Обчислюється точність оцінки .

5. Визначається надійний інтервал .

Приклад 2.7. За даними вибірки об’єму одержаною із генеральної сукупності, розподіленої за нормальним законом з невідомим математичним сподіванням а і невідомим середнім квадратичним відхиленням , оцінимо невідоме генеральне середнє арифметичне (математичне сподівання ) по вибірковій середній і знайдемо для нього надійний інтервал з імовірністю .

Розв’язання. Змоделюємо за допомогою функції вибірку Х об’єму , розподілену за нормальним законом з параметрами . За даними цієї вибірки знаходимо вибіркове середнє і середнє квадратичне відхилення . За допомогою квантиля розподілу Стьюдента визначаємо точність оцінки і знаходимо відповідний надійний інтервал для математичного сподівання а.

Алгоритм у Mathcad

_{Початкові дані моделі}

_{Моделювання вибірки}

_{Фрагмент вибірки}

_{Вибіркові числові характеристики}

_{Квантиль розподілу Стьюдента}

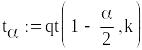
_{Точність оцінки}

Границі надійного інтервалу

Надійний інтервал

_◄

2.5.4. Надійний інтервал для генерального середнього

при малій вибірці

На практиці часто доводиться мати справу з вибірками невеликого об’єму . У цьому випадку наведений вище наближений метод побудови інтервальної оцінки для генеральної середньої не застосовний у силу двох обставин:

• не обгрунтованим стає припущення про нормальний розподіл вибіркової середньої 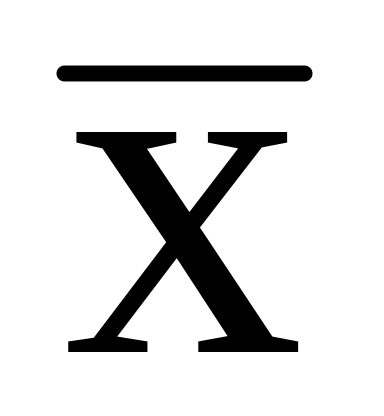, оскільки воно базується на центральній граничній теоремі при великих n;

• не обгрунтованою стає заміна невідомої генеральної дисперсії на її точкову оцінку 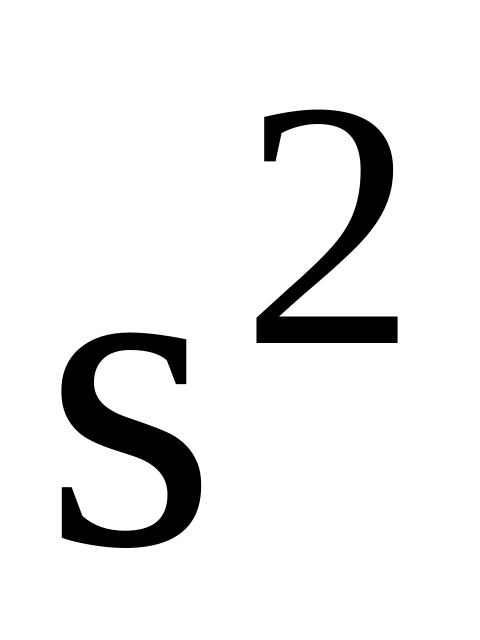, оскільки в силу закону великих чисел ця заміна можлива лише при великих n.

Задача побудови надійного інтервалу для генеральної середньої при малих вибірках може бути вирішена, якщо генеральна сукупність розглядуваної ознаки має нормальний розподіл.

Якщо ознака (випадкова величина Х) має нормальний розподіл з параметрами , , тобто , то вибіркова середня при будь-якому (а не тільки при ) має нормальний розподіл .

Таким чином, якщо була б відома генеральна дисперсія то надійний інтервал для математичного сподівання при малих можна було б побудувати аналогічно вище наведеному алгоритму. Зауважимо, що у цьому випадку нормальне відхилення вибіркового середнього

має стандартний нормальний розподіл , тобто нормальний розподіл з математичним сподіванням 0 і дисперсією 1.

Дійсно, використовуючи властивості математичного сподівання і дисперсії, одержимо:

,

.

Однак на практиці майже завжди генеральна дисперсія (як і оцінювана середня а) невідома. Якщо заміна її “найкращою” оцінкою по вибірці, а саме, виправленою вибірковою дисперсією , то інтерес представляє розподіл вибіркової характеристики (статистики)

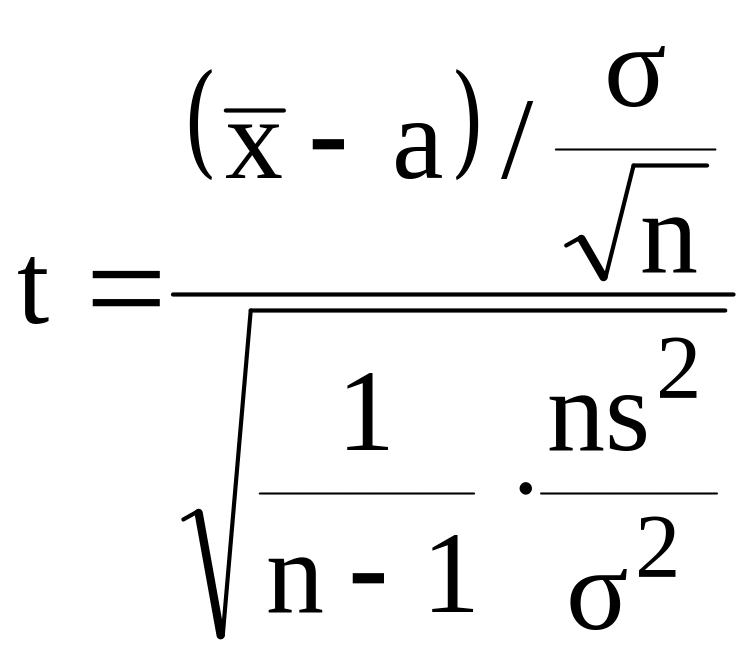. (2.50)

Чисельник виразу, як показано вище, має стандартний нормальний розподіл . Доведено, що випадкова величина має - розподіл з ступенями свободи. Цей розподіл не залежить від невідомих параметрів розподілу випадкової величини Х, а залежить від числа , яке називається числом ступенів свободи.

Число ступенів свободи визначається як загальне число n спостережень (варіант) випадкової величини Х мінус кількість рівнянь m, які пов’язують ці спостереження, тобто .

Так, наприклад, при визначенні числа ступенів свободи розподілу статистики одна ступінь свободи „губиться” при визначені вибіркової середньої (n спостережень пов’язані з одним рівнянням ).

Використовуючи -розподіл Стьюдента, можна знайти таке критичне значення що ймовірність того, що статистика за абсолютною величиною не перевищить величину дорівнює :

(2.60)

У Mathcad квантиль -розподілу Стьюдента визначається за функцією у вигляді

, де . (2.61)

Формула (2.39) для визначення надійного інтервалу для малої вибірки може бути представлена у вигляді:

, (2.62)

де – функція -розподілу Стьюдента, – гранична похибка малої вибірки. Надійний інтервал для генерального середнього, як і раніше, знаходиться за формулою:

(2.63)