2.5.5. Надійний інтервал для дисперсії нормального розподілу при відомому математичному сподіванні

Статистична модель. Нехай розподіл ознаки Х у генеральній сукупності є нормальним з параметрами а і Припустимо, що математичне сподівання (генеральне середнє) відоме. Потрібно знайти надійний інтервал для невідомої дисперсії і середнього квадратичного відхилення нормально розподіленої випадкової величини Х, якщо відоме її математичне сподівання а із заданим рівнем значущості .

Розглянемо вибіркову дисперсію повторної вибірки , яка характеризує варіацію ознаки відносно генеральної середньої а:

або

Для побудови відповідних надійних інтервалів введемо статистику

.

Враховуючи, що , , , легко показати, що , . Отже, величини мають нормований нормальний розподіл

Відомо, що розподіл суми квадратів n незалежних випадкових величин , кожна з яких має стандартний нормальний розподіл , представляє розподіл з ступенями свободи.

Таким чином, статистика має розподіл з ступенями свободи. Розподіл не залежить від невідомих параметрів випадкової величини , а залежить лише від числа ступенів свободи . Критичне значення , для якого ймовірність того, що випадкова величина, яка має - розподіл з ступенями свободи перевищить , тобто

визначається квантилем - розподілу.

Якщо – повторна вибірка із нормально розподіленої генеральної сукупності, то випадкова величина або має розподіл з ступенями свободи. Тому для заданої довірчої ймовірності можна записати

. (2.64)

Величини звичайно вибирають таким чином, щоб імовірності подій і були однакові:

.

Перетворивши подвійну нерівність в дужках у (2.64) до еквівалентного вигляду

,

одержимо формулу для надійної ймовірності для генеральної дисперсії:

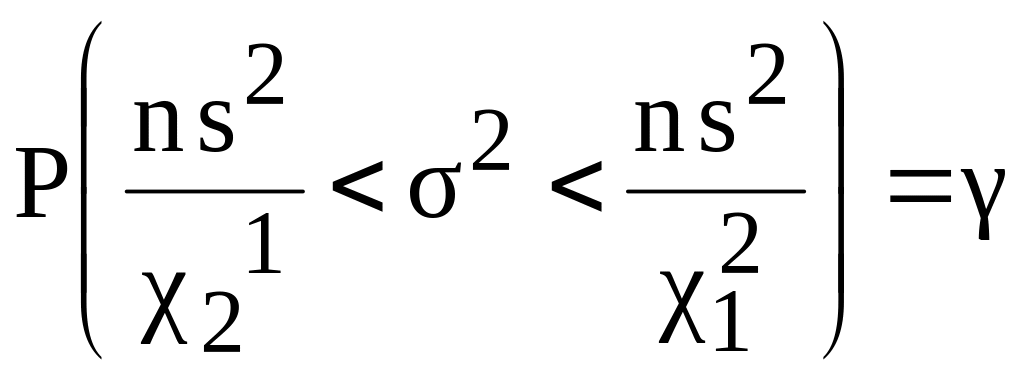, (2.65)

а також для середнього квадратичного відхилення

. (2.66)

У величини і обчислюються як квантилі порядку і розподілу з ступенями свободи за допомогою функції .

При використанні функції слід враховувати, що . Оскільки , то умова рівносильна умові

.

Таким чином, критичні значення знаходимо із виразів

(2.67)

Нижня і відповідно верхня границі надійного інтервалу для дисперсії дорівнюватимуть

(2.68)

Аналогічно для середнього квадратичного відхилення

(2.69)

2.5.6. Надійний інтервал для дисперсії нормального розподілу при невідомому математичному сподіванні

У практиці статистичного аналізу математичне сподівання , як правило, невідоме і доводиться мати справу не з середнім квадратичним відхиленням відповідно генеральної середньої а, а із вибірковою середньою , отже, і з вибірковою дисперсією або з виправленою дисперсією .

Статистична модель. Нехай розподіл ознаки Х у генеральній сукупності є нормальним з параметрами а і Припустимо, що математичне сподівання (генеральне середнє) невідоме. Потрібно із заданим рівнем значущості знайти надійні інтервали для невідомої дисперсії і середнього квадратичного відхилення цієї випадкової величини Х.

Визначимо для оцінку

,

де – оцінка невідомого математичного сподівання а.

Для побудови надійного інтервалу для дисперсії задамося рівнем значущості і визначимо величини так, щоб виконувались умови

.

Тоді

.

Звідси з імовірністю маємо нерівності

тобто

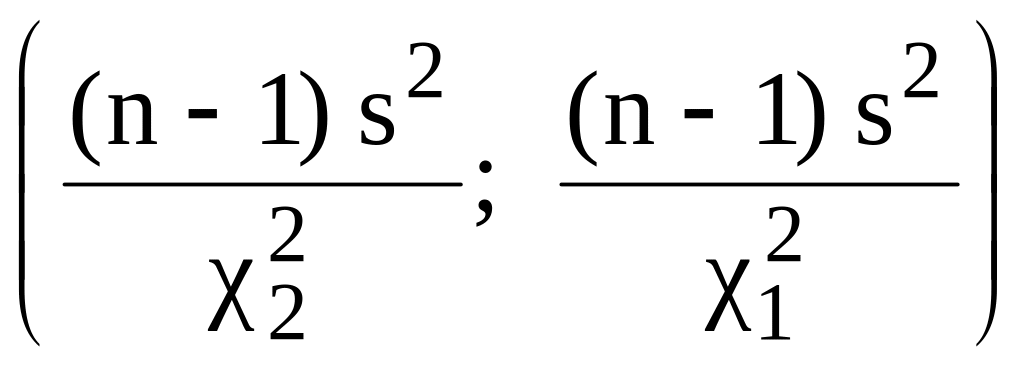(2.70)

– надійний інтервал для невідомої дисперсії при невідомому математичному сподіванні а.

Аналогічно надійний інтервал для середнього квадратичного відхилення при невідомому математичному сподіванні буде мати вигляд

. (2.71)

Критичні значення обчислюються як квантилі відповідного порядку з ступенями свободи. У Mathcad ці величини обчислюються відповідно за функціями .

При кількості ступенів свободи можна вважати, що випадкова величина має стандартний нормальний розподіл . Тому для визначення і слід записати:

, (2.72)

звідки і після перетворень одержуємо нерівність

Таким чином, при розрахунку надійного інтервалу треба покладати

, , (2.73)

де , тобто є квантиль розподілу і визначається за функцією Mathcad .

Знання точного значення математичного сподівання у загальному випадку несуттєво зменшує довжину надійного інтервалу у порівнянні надійним інтервалом, визначеним без використання точного значення математичного сподівання. Тому, якщо є сумніви у точному значенні математичного сподівання, слід використовувати метод побудови надійних інтервалів із невідомим математичним сподіванням.

Алгоритм побудови надійного інтервалу

1. Обчислюються точкові оцінки .

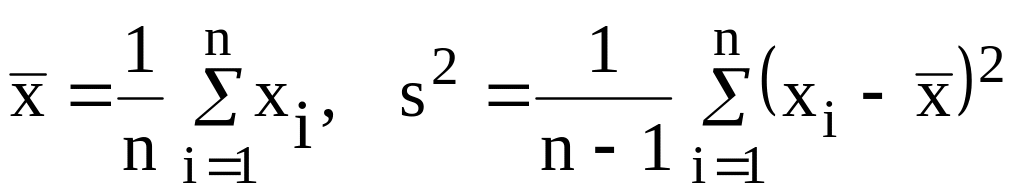2. Задається рівень значущості (довірча імовірність ).

3. Визначаються квантилі , де – функція, обернена до функції розподілу з ступенями свободи. У квантилі і обчислюються за функцією .

4. Обчислюються нижня і верхня оцінки точності для дисперсії і середнього квадратичного відхилення і _.

5. Визначаються надійні інтервали для дисперсії і середнього квадратичного відхилення.

Коментар. Метод не стійкий при відхиленні від нормальності.

Приклад 2.8. За даними вибірки об’єму одержаною із генеральної сукупності, розподіленої за нормальним законом з невідомим математичним сподіванням а і невідомим середнім квадратичним відхиленням , оцінимо невідоме генеральне середнє квадратичне відхилення за вибірковим середнім квадратичним відхиленням і знайдемо для нього надійний інтервал з імовірністю .

Розв’язання. Змоделюємо за допомогою функції вибірку Х об’єму , розподілену за нормальним законом з параметрами . За даними цієї вибірки знаходимо вибіркове середнє і середнє квадратичне відхилення . За допомогою квантиля розподілу визначаємо точність оцінки і знаходимо відповідний надійний інтервал для середнього квадратичного відхилення

Алгоритм у Mathcad

Початкові дані моделі

_{Моделювання вибірки}

_{Фрагмент вибірки}

_{Вибіркові оцінки математичного сподівання і середнього квадратичного відхилення}

Квантилі -розподілу

_{Точність нижньої і верхньої оцінки середнього квадратичного відхилення}

Надійний інтервал для середнього квадратичного відхилення з рівнем значущості

_◄