- •1.Определения и вычисление 2 и 3го порядка. Свойства определителей.
- •2.Матрицы,основные определения. Действия над матрицами.
- •3.Определение минора элемента, алгебраического дополнения.
- •4.Понятие обратной матрицы. Теорема об ее вычислении.
- •5.Понятие о ранге матрицы.
- •6.Системы линейных уравнений. Основные понятия.
- •7.Системы линейных однородных уравнений. Методы решения.
- •8.Правило Крамера.
- •Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •9.Метод Гаусса.
- •10) Решение линейных систем с помощью обратной матрицы.
- •11)Векторы. Основные определения. Сложение и вычитание векторов.
- •12)Умножение вектора на скаляр. Коллинеарные вектора. Необходимое и достаточное условия коллинеарности векторов.
- •13)Определение проекции вектора на ось. Теоремы о проекциях. Вектор в трехмерном пространстве. Направляющие косинусы. Разложение вектора по ортам.
- •14) Линейная зависимость и независимость векторов.
- •15)Скалярное произведение векторов. Геометрический и механический смысл. Свойства. Таблица умножения ортов. Угол между векторами.
- •16)Понятие тройки векторов. Левая, правая тройка, Определение векторного произведения. Геометрический смысл. Свойства. Векторное произведение в декартовых координатах.
- •17) Смешанное произведение векторов. Свойства и геометрический смысл. Компланарные векторы.
- •18) Полярная система координат
- •19) Прямая на плоскости. Общее уравнение прямой. Частные случаи. Расположение двух прямых на плоскости.
- •20)Эллипс.
- •21)Гипербола.
- •22)Парабола.
- •23)Уравнение линии и поверхности в пространстве.
- •24)Плоскость. Общее уравнение. Случаи расположения 2-х плоскостей в пространстве. Уравнение плоскости, проходящей через 3 точки.
- •25.Уравнение прямой в пространстве. Случаи расположения двух прямых. Угол между прямой и плоскостью. Формула расстояния от точки до плоскости.
- •26. Поверхности второго порядка. Построение методом сечений.
- •27.Определение функции. Способы задания. Классификация.
- •28.Предел числовой последовательности. Основные определения. Теорема об ограниченной последовательности.
- •29. Основные теоремы о пределах.
- •30.Определение множества и ограниченного множества. Супремум. Инфимум.
- •Ограниченное числовое множество.
- •Ограниченное множество в метрическом пространстве
- •Ограниченность в частично упорядоченном множестве
- •31.Определение предела числовой последовательности. Признаки существования предела, теорема о зажатой последовательности.
- •32.Предел функции. Теоремы о пределах. Способы вычисления пределов.
- •Алгоритм решения.
- •33.Определение предела функции. 1 и 2 замечательный предел.
- •Бесконечно большие f(X) и g(X) считаются величинами одного порядка, если
- •Если , то f(X) считается бесконечно большой более высокого порядка, чем g(X).
- •Бесконечно большая f(X) называется величиной k-го порядка относительно бесконечно большой g(X), если .
- •35.Односторонние пределы функции. Определение. Непрерывность функции в точке.
- •36.Непрерывность функции в точке.
- •37.Понятие проивзодной,ее физический и геометрический смысл.
- •38. Определение производной. Правило дифференцирования суммы и частного функции, разности и произведения функций.
- •39.Правило дифференцирования сложной функции. Теорема о производной обратной функции. Дифференцирование функции, заданной неявно. Понятие логарифмической производной.
- •40.Нахождение производной функции, заданной параметрически.
- •41.Дифференциал. Определение ,свойства, геометрический смысл.
- •42.Дифференциалы и производные высших порядков.
- •43.Теоремы Ферма, Ролля, Лагранжа и Коши и их геометрический смысл.
- •44.Правило Лопиталя. Следствие о раскрытии неопределенностей разных видов.
- •45.Формула Тейлора.
- •46.Выпуклость и вогнутость кривых. Определение. Определение точки перегиба.
- •47.Асимпоты. Определение. Классификация.
- •48.Комплескные числа.
- •49.Функции нескольких переменных.
- •50.Предел функции двух переменных. Непрерывные функции, частные производные.
- •51.Полный дифференциал. Производные сложной функции.
- •52.Неявные функции и их дифференцирование.
- •53.Касательная плоскость и нормаль к поверхности. Частные производные.
- •54.Дифференциалы высших порядков.
- •55.Первообразная функция и неопределенный интеграл .Свойства неопределенного интеграла.
- •56.Интегрирование методом замены и внесения под знак дифференциала.
- •57.Интегрирование по частям.
- •58. Интегрирование рациональных функций.
- •59.Интегрирование иррациональных функций.
- •1. Сделаем замену , тогда , а . Следовательно,
- •2. . Так как , а , выберем в качестве новой переменной . Тогда . Поэтому
- •60.Интегрирование тригонометрических функций.
49.Функции нескольких переменных.
Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.
Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.
Обозначения: z = f(x,y), z = z(x,y).
Примеры.
z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.
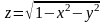 -
функция, областью определения которой
являются решения неравенства
-
функция, областью определения которой
являются решения неравенства
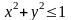 .
.
Замечание.
Так как пару чисел (х,у)
можно считать координатами некоторой
точки на плоскости, будем впоследствии
использовать термин «точка» для пары
аргументов функции двух переменных, а
также для упорядоченного набора чисел
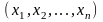 ,
являющихся аргументами функции нескольких
переменных.
,
являющихся аргументами функции нескольких
переменных.
Определение
1.3. .
Переменная z
(с областью
изменения Z)
называется
функцией
нескольких независимых переменных
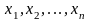 в множестве М,
если каждому набору чисел
из
множества М
по некоторому правилу или закону ставится
в соответствие одно определенное
значение z
из Z.
Понятия
аргументов и области определения
вводятся так же, как для функции двух
переменных.
в множестве М,
если каждому набору чисел
из
множества М
по некоторому правилу или закону ставится
в соответствие одно определенное
значение z
из Z.
Понятия
аргументов и области определения
вводятся так же, как для функции двух
переменных.
Обозначения: z = f , z = z .
Геометрическое изображение функции двух переменных.
Рассмотрим функцию z = f(x,y), (1.1)
о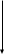 пределенную
в некоторой области М
на плоскости Оху.
Тогда множество точек трехмерного
пространства с координатами (x,y,z),
где
пределенную
в некоторой области М
на плоскости Оху.
Тогда множество точек трехмерного
пространства с координатами (x,y,z),
где
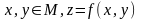 ,
является графиком функции двух переменных.
Поскольку уравнение (1.1) определяет
некоторую поверхность в трехмерном
пространстве, она и будет геометрическим
изображением рассматриваемой функции.
,
является графиком функции двух переменных.
Поскольку уравнение (1.1) определяет
некоторую поверхность в трехмерном
пространстве, она и будет геометрическим
изображением рассматриваемой функции.



 z
z
z = f(x,y)

 M
y
M
y
Примерами могут служить изучаемые в предыдущем семестре уравнения плоскости
z = ax + by + c
и поверхностей второго порядка:
z = x² + y² (параболоид вращения),
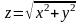 (конус) и т.д.
(конус) и т.д.
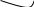

 Замечание.
Для функции трех и более переменных
будем пользоваться термином «поверхность
в n-мерном
пространстве», хотя изобразить подобную
поверхность невозможно.
Замечание.
Для функции трех и более переменных
будем пользоваться термином «поверхность
в n-мерном
пространстве», хотя изобразить подобную
поверхность невозможно.
50.Предел функции двух переменных. Непрерывные функции, частные производные.
Число А называется пределом функции нескольких переменных f в точке М0, если такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.
Обозначения:
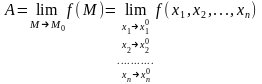 .
.
Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри δ-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности.
Примеры.
Покажем, что функция
 не имеет предела при М→О(0,0).
Действительно, если в качестве линии,
по которой точка М
приближается к началу координат, выбрать
прямую у =
х, то на этой
прямой
не имеет предела при М→О(0,0).
Действительно, если в качестве линии,
по которой точка М
приближается к началу координат, выбрать
прямую у =
х, то на этой
прямой
 .
Если же траекторией движения считать
прямую у =
2х,
то
.
Если же траекторией движения считать
прямую у =
2х,
то
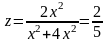 .
Следовательно, предел в точке (0,0) не
существует.
.
Следовательно, предел в точке (0,0) не
существует.Найдем повторные пределы функции
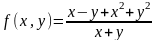 при х→0,
у→0.
при х→0,
у→0.
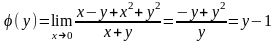 ,
,
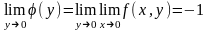 .
Если же произвести предельные переходы
в обратном порядке, получим:
.
Если же произвести предельные переходы
в обратном порядке, получим:
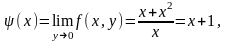
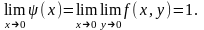 Таким
образом, повторные пределы оказались
различными (откуда следует, конечно,
что функция не имеет в точке (0,0) предела
в обычном смысле).
Таким
образом, повторные пределы оказались
различными (откуда следует, конечно,
что функция не имеет в точке (0,0) предела
в обычном смысле).
Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.
Функция
f
называется непрерывной
в точке М0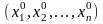 ,
если
,
если
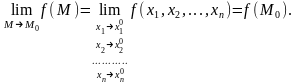 (1.2)
(1.2)
Если
ввести обозначения
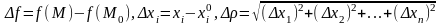 ,
то условие (1.2) можно переписать в форме
,
то условие (1.2) можно переписать в форме
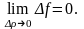 (1.3)
(1.3)
Частные производные.
Рассмотрим
изменение функции
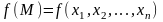 при задании приращения только одному
из ее аргументов – хi
, и назовем его
при задании приращения только одному
из ее аргументов – хi
, и назовем его
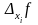 .
.
Частной
производной
функции
по
аргументу хi
называется
 .
.
Обозначения:
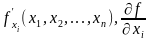 .
.
Таким образом, частная производная функции нескольких переменных определяется фактически как производная функции одной переменной – хi. Поэтому для нее справедливы все свойства производных, доказанные для функции одной переменной.
Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными.
Примеры.
1.
z
= 2x²
+ 3xy
–12y²
+ 5x
– 4y
+2,
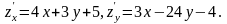
2.
z =
xy,
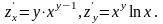
3.