
- •1.Определения и вычисление 2 и 3го порядка. Свойства определителей.
- •2.Матрицы,основные определения. Действия над матрицами.
- •3.Определение минора элемента, алгебраического дополнения.
- •4.Понятие обратной матрицы. Теорема об ее вычислении.
- •5.Понятие о ранге матрицы.
- •6.Системы линейных уравнений. Основные понятия.
- •7.Системы линейных однородных уравнений. Методы решения.
- •8.Правило Крамера.
- •Если система (2.3) имеет единственное решение, определяемое по формулам: .
- •9.Метод Гаусса.
- •10) Решение линейных систем с помощью обратной матрицы.
- •11)Векторы. Основные определения. Сложение и вычитание векторов.
- •12)Умножение вектора на скаляр. Коллинеарные вектора. Необходимое и достаточное условия коллинеарности векторов.
- •13)Определение проекции вектора на ось. Теоремы о проекциях. Вектор в трехмерном пространстве. Направляющие косинусы. Разложение вектора по ортам.
- •14) Линейная зависимость и независимость векторов.
- •15)Скалярное произведение векторов. Геометрический и механический смысл. Свойства. Таблица умножения ортов. Угол между векторами.
- •16)Понятие тройки векторов. Левая, правая тройка, Определение векторного произведения. Геометрический смысл. Свойства. Векторное произведение в декартовых координатах.
- •17) Смешанное произведение векторов. Свойства и геометрический смысл. Компланарные векторы.
- •18) Полярная система координат
- •19) Прямая на плоскости. Общее уравнение прямой. Частные случаи. Расположение двух прямых на плоскости.
- •20)Эллипс.
- •21)Гипербола.
- •22)Парабола.
- •23)Уравнение линии и поверхности в пространстве.
- •24)Плоскость. Общее уравнение. Случаи расположения 2-х плоскостей в пространстве. Уравнение плоскости, проходящей через 3 точки.
- •25.Уравнение прямой в пространстве. Случаи расположения двух прямых. Угол между прямой и плоскостью. Формула расстояния от точки до плоскости.
- •26. Поверхности второго порядка. Построение методом сечений.
- •27.Определение функции. Способы задания. Классификация.
- •28.Предел числовой последовательности. Основные определения. Теорема об ограниченной последовательности.
- •29. Основные теоремы о пределах.
- •30.Определение множества и ограниченного множества. Супремум. Инфимум.
- •Ограниченное числовое множество.
- •Ограниченное множество в метрическом пространстве
- •Ограниченность в частично упорядоченном множестве
- •31.Определение предела числовой последовательности. Признаки существования предела, теорема о зажатой последовательности.
- •32.Предел функции. Теоремы о пределах. Способы вычисления пределов.
- •Алгоритм решения.
- •33.Определение предела функции. 1 и 2 замечательный предел.
- •Бесконечно большие f(X) и g(X) считаются величинами одного порядка, если
- •Если , то f(X) считается бесконечно большой более высокого порядка, чем g(X).
- •Бесконечно большая f(X) называется величиной k-го порядка относительно бесконечно большой g(X), если .
- •35.Односторонние пределы функции. Определение. Непрерывность функции в точке.
- •36.Непрерывность функции в точке.
- •37.Понятие проивзодной,ее физический и геометрический смысл.
- •38. Определение производной. Правило дифференцирования суммы и частного функции, разности и произведения функций.
- •39.Правило дифференцирования сложной функции. Теорема о производной обратной функции. Дифференцирование функции, заданной неявно. Понятие логарифмической производной.
- •40.Нахождение производной функции, заданной параметрически.
- •41.Дифференциал. Определение ,свойства, геометрический смысл.
- •42.Дифференциалы и производные высших порядков.
- •43.Теоремы Ферма, Ролля, Лагранжа и Коши и их геометрический смысл.
- •44.Правило Лопиталя. Следствие о раскрытии неопределенностей разных видов.
- •45.Формула Тейлора.
- •46.Выпуклость и вогнутость кривых. Определение. Определение точки перегиба.
- •47.Асимпоты. Определение. Классификация.
- •48.Комплескные числа.
- •49.Функции нескольких переменных.
- •50.Предел функции двух переменных. Непрерывные функции, частные производные.
- •51.Полный дифференциал. Производные сложной функции.
- •52.Неявные функции и их дифференцирование.
- •53.Касательная плоскость и нормаль к поверхности. Частные производные.
- •54.Дифференциалы высших порядков.
- •55.Первообразная функция и неопределенный интеграл .Свойства неопределенного интеграла.
- •56.Интегрирование методом замены и внесения под знак дифференциала.
- •57.Интегрирование по частям.
- •58. Интегрирование рациональных функций.
- •59.Интегрирование иррациональных функций.
- •1. Сделаем замену , тогда , а . Следовательно,
- •2. . Так как , а , выберем в качестве новой переменной . Тогда . Поэтому
- •60.Интегрирование тригонометрических функций.
44.Правило Лопиталя. Следствие о раскрытии неопределенностей разных видов.
Если функции f(x) и g(x) удовлетворяют на некотором отрезке [ab] условиям теоремы Коши и f(a) = g(a) = 0, то отношение f(x)/g(x) не определено при х=а, но определено при остальных значениях х. Поэтому можно поставить задачу вычисления предела этого отношения при x→a. Вычисление таких пределов называют обычно «раскрытием неопределенностей вида {0/0}».
Теорема
20.3 (правило Лопиталя).
Пусть функции f(x)
и g(x)
удовлетворяют
на отрезке [ab]
условиям теоремы Коши и f(a)=g(a)=0.
Тогда, если
существует
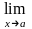
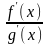 , то существует и
, то существует и
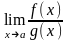 ,
причем
,
причем
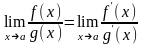 .
(20.2)
.
(20.2)
Доказательство.
Выберем
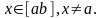 Из теоремы Коши следует, что
Из теоремы Коши следует, что
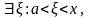 такое, что
такое, что
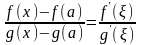 .
По условию теоремы f(a)=g(a)=0,
поэтому
.
По условию теоремы f(a)=g(a)=0,
поэтому
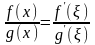 .
При
.
При
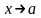
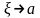 .
При этом, если существует
.
При этом, если существует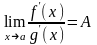 ,
то существует и
,
то существует и
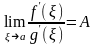 .
Поэтому
.
Поэтому
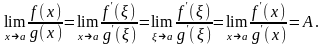 Теорема доказана.
Теорема доказана.
Пример.
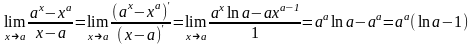 при a>0.
при a>0.
Замечание 1. Если f(x) или g(x) не определены при х=а, можно доопределить их в этой точке значениями f(a)=g(a)=0. Тогда обе функции будут непрерывными в точке а, и к этому случаю можно применить теорему 20.3.
Замечание
2. Если
f′(a)=g′(a)=0
и f′(x)
и g′(x)
удовлетворяют
условиям, наложенным в теореме 20.3 на
f(x)
и
g(x),
к отношению
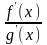 можно еще раз применить правило Лопиталя:
можно еще раз применить правило Лопиталя:
 и так далее.
и так далее.
Пример.
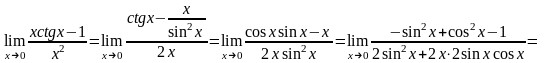
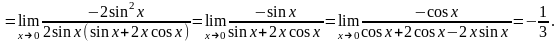
Правило
Лопиталя можно применять и для раскрытия
неопределенностей вида
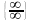 ,
то есть для вычисления предела отношения
двух функций, стремящихся к бесконечности
при
,
то есть для вычисления предела отношения
двух функций, стремящихся к бесконечности
при
Теорема
20.4. Пусть
функции f(x)
и g(x)
непрерывны и дифференцируемы при
 в окрестности точки а,
причем
в окрестности точки а,
причем
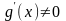 в этой окрестности. Тогда, если
в этой окрестности. Тогда, если
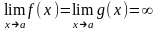 и существует
,
то существует и
,
причем
и существует
,
то существует и
,
причем
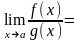 .
.
Доказательство.
Выберем
в рассматриваемой окрестности точки а
точки α и х
так, чтобы
α < x
< a
(или a
< x
< α). Тогда
по теореме Коши существует точка с
(a
< c
< x)
такая, что
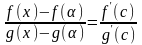 .
Так как
.
Так как
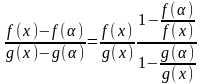 ,
получаем:
,
получаем:
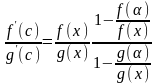 ,
откуда
,
откуда
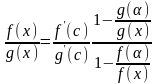 .
(20.3) Так как
,
можно для любого малого ε выбрать α
настолько близким к а,
что для любого с
будет выполняться неравенство
.
(20.3) Так как
,
можно для любого малого ε выбрать α
настолько близким к а,
что для любого с
будет выполняться неравенство
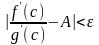 ,
,
или
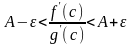 .
(20.4) Для этого же значения
ε из условия теоремы следует, что
.
(20.4) Для этого же значения
ε из условия теоремы следует, что
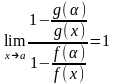 (так как
),
поэтому
(так как
),
поэтому
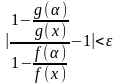 ,
или
,
или
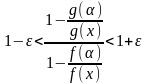 .
(20.5)
.
(20.5)
Перемножив неравенства (20.4) и (20.5), получим
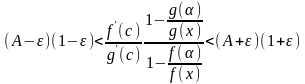 ,
или, после использования равенства
(20.3):
,
или, после использования равенства
(20.3):
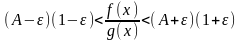 .
Поскольку ε – произвольно малое число,
отсюда следует, что
А=
.
Поскольку ε – произвольно малое число,
отсюда следует, что
А=
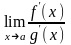 ,
что и требовалось доказать.
,
что и требовалось доказать.
Замечание
1. Теорема 20.4 верна и при А=
.
В этом случае
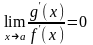 .
Тогда и
.
Тогда и
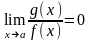 ,
следовательно,
,
следовательно,
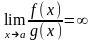 .
.
Замечание
2. Теоремы 20.3 и 20.4 можно доказать и для
случая, когда
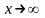 .
.
Пример.
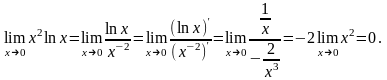
45.Формула Тейлора.
Рассмотрим функцию y=f(x), имеющую в окрестности точки х=а все производные до порядка (n+1) включительно, и поставим задачу: найти многочлен y=Pn(x) степени не выше n, для которого его значение в точке а, а также значения его производных по n-й порядок равны значениям при x=a выбранной функции и ее производных соответствующего порядка:
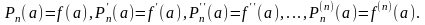 (21.1)
(21.1)
Пусть искомый многочлен имеет вид:
Pn(x)=C0+C1(x-a)+C2(x-a)²+…+Cn(x-a)n. (21.2)
При этом
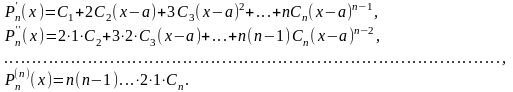
Тогда
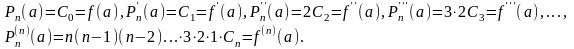 (21.3)
(21.3)
Из формул (21.3) можно выразить коэффициенты Сi через значения производных данной функции в точке а.
Замечание. Произведение последовательных натуральных чисел 1∙2∙3∙…∙(n-1)n называется факториалом числа n и обозначается
n! = 1∙2∙3∙…∙(n-1)n . (21.4)
Дополнительно вводится 0!=1.
Используя это обозначение, получим:
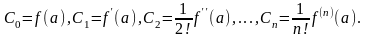 (21.5)
(21.5)
Таким образом, искомый многочлен имеет вид:
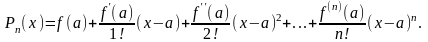 (21.6)
(21.6)
Обозначим через Rn(x) разность значений данной функции f(x) и построенного многочлена Pn(x): Rn(x) = f(x) – Pn(x), откуда f(x) = Pn(x) + Rn(x) или
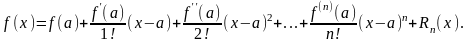 (21.7)
(21.7)
Полученное представление функции называется формулой Тейлора, а Rn(x) называется остаточным членом формулы Тейлора. Для тех значений х, для которых Rn(x) мало, многочлен Pn(x) дает приближенное представление функции f(x). Следовательно, формула (21.7) дает возможность заменить функцию y = f(x) многочленом y = Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn(x).
