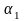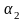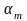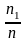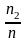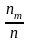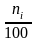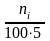Раздел 14. Элементы математической статистики.

Математическая статистика – раздел математики, изучающий математические методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей. Математическая статистика опирается на теорию вероятностей.

§1.Выборка. Обработка результатов.

В любой практической деятельности значительную роль играют статистические методы изучения случайных явлений. К этим методам прибегают всякий раз, когда требуется изучить распределение большой совокупности предметов, явлений, индивидуумов по некоторым признакам. Так как практически любой признак допускает количественную оценку, то можно говорить о распределении некоторой случайной величины Х.

Все возможные значения случайной величины Х называются генеральной совокупностью.

Способ «поголовного» обследования всей изучаемой совокупности связан с рядом трудностей. Поэтому обследование генеральной совокупности заменяют обследованием некоторой её наудачу выбранной части, которая называется выборкой или выборочной совокупностью.

Объёмом выборочной или генеральной совокупности называется число объектов этой совокупности.

Чтобы в выборке могли проявиться закономерности, существующие в генеральной совокупности, выборка должна быть достаточно большой, и все объекты генеральной совокупности должны иметь одинаковую вероятность попасть в выборку. При этом объекты выборки должны отбираться независимо друг от друга.

К сожалению, на практике не уделяют достаточного внимания анализу независимости отдельных измерений, что может привести к неприменимости выводов статистической теории.

Итак, предположим, что изучается некоторая случайная величина Х. С этой целью проводятся n независимых опытов (наблюдений), в результате которых величина Х приняла n числовых значений (статистические данные): х₁, х₂,…,х_n

Совокупность этих значений и есть произведённая нами выборка. n – объём выборки.

Первый этап обработки – это составление вариационного ряда: из выборки отбирают все различные значения и располагают их в порядке возрастания: 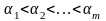,где 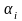– варианты.

Второй этап обработки – составление эмпирического (то есть полученного опытным путём) закона распределения. Форма его зависит от характера изучаемой случайной величины.

Пусть Х – дискретная случайная величина. Тогда естественной формой эмпирического закона распределения является таблица относительных частот, показывающая, с какой частотой наблюдалось то или иное значение.

Таблица частот имеет вид:

		….
		…

В первой строке – числа вариационного ряда, а во второй – их относительные частоты 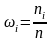, где n – число всех опытов, n_i – число опытов, в которых наблюдалось значение . Очевидно, что .

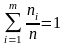Можно ожидать, что с увеличением числа опытов таблица частот будет все более приближаться к истинному закону распределения случайной величины Х.

Если на плоскости в прямоугольной системе координат соединить последовательно точки (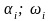 ) , то получим ломаную, называемую полигоном частот.

Пример 1. По журналу собраны данные о числе пропущенных занятий по математике у 25 студентов второго курса. В итоге получены значения: 2, 6, 0, 2, 6, 3, 0, 2, 6, 4, 0, 3, 3, 2, 2, 4, 0, 0, 2, 3, 6, 0, 3, 0, 2.

Здесь объем выборки n=25, а вариационный ряд состоит из пяти различных чисел (вариант): 0, 2, 3, 4, 6. Найдем относительную частоту появления каждого из чисел и составим таблицу частот:

0	2	3	4	6
7/25	7/25	5/25	2/25	4/25

Полигон частот:

Пусть Х – непрерывная случайная величина.

Пользоваться таблицей частот в прежнем её виде уже не имеет смысла. В этом случае составляют интервальную таблицу частот .

Диапазон изменения случайной величины Х разбивают на l интервалов [c₁;c₂], [c₂;c₃],…,[c_l,c_l+1].

Находим n_i – количество значений Х, лежащих в i-ом интервале и определяют частоту попадания в i-интервал .

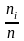Возникает вопрос, если значение попало на границу двух интервалов, то к какому его отнести? Это безразлично. Условимся относить к левому.

Интервальная таблица частот тогда имеет вид:

(с1;с2]	(с2;с3]	…	(сl;сl+1]
n1/n	n2/n	…	nl/n

Интервальная таблица частот изображается графически в виде гистограммы.

Это ступенчатая фигура, состоящая из прямоугольников с основанием [с_i;с_i+1] и площадью n_i/n, т.е. высоты прямоугольников

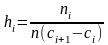- плотность частоты попадания в i- интервал.

Вероятностный смысл гистограммы: верхняя ступенчатая линия гистограммы приближенно представляет плотность распределения вероятности случайной величины Х.

Число интервалов следует брать не очень большим, чтобы после группировки вариационный ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака.

В литературе по статистической обработке экспериментальных данных рекомендуется выбирать количество интервалов (равной длины) в пределах:

, где п – объем выборки.

Пример 2. Расстояние до цели измеряется радиодальномером. Случайная величина Х – ошибка измерения расстояния. С целью установления точности прибора произведено п=100 измерений этой ошибки (в метрах):

ошибка (м)	(-20;-15]	(-15;-10]	(-10;-5]	(-5;0]	(0;5]	(5;10]	(10;15]
число ошибок ni	8	11	18	26	19	12	6

Построим гистограмму распределения.

Для этого составим интервальную таблицу частот, найдем плотность частоты попадания в каждый интервал:

ошибка (м)	(-20;-15]	(-15;-10]	(-10;-5]	(-5;0]	(0;5]	(5;10]	(10;15]
число ошибок ni	8	11	18	26	19	12	6
относительная частота =	0,08	0,11	0,18	0,26	0,19	0,12	0,06
плотность частоты hi=	0,016	0,022	0,036	0,052	0,038	0,024	0,012

Построение гистограммы частот - на каждом i-ом интервале как на основании строим прямоугольник высоты h_i :

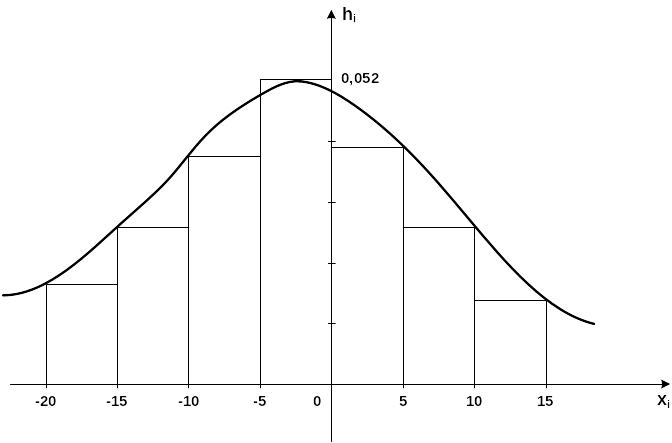
Из рисунка видно, что распределение величины Х (ошибки измерений) по форме близко к нормальному.