
- •Раздел 14. Элементы математической статистики.
- •§1.Выборка. Обработка результатов.
- •§ 2.Эмпирическая функция распределения.
- •§ 3 Оценки параметров.
- •Оценка для математического ожидания.
- •Оценки для дисперсии.
- •Оценки для среднего квадратического отклонения.
- •Оценки для моментов случайной величины.
- •§4. Методы нахождения оценок.
- •§5. Доверительные интервалы.
- •Доверительный интервал для m при неизвестном σ.
- •§6. Понятие о статистических гипотезах.
Оценка для математического ожидания.
Рассмотрение конкретных оценок мы начинаем с наиболее важного случая -оценки для математического ожидания.
Пусть в результате n испытаний случайная величина X принимает значения
, ,…, .
В
качестве оценки для математического
ожидания естественно принять выборочное
среднее
(эмпирическое среднее):
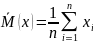 .
.
Или
выборочное среднее :
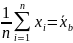
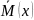 также случайная
величина (т.к. зависит от случайных
значений выборки), поэтому найдем для
нее математическое ожидание:
также случайная
величина (т.к. зависит от случайных
значений выборки), поэтому найдем для
нее математическое ожидание:
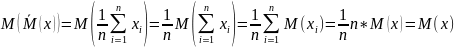
Следовательно, оценка является несмещённой.
Найдем теперь дисперсию:
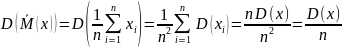
Как видно, дисперсия стремится к 0 при n, стремящемся к ∞. Следовательно, оценка является состоятельной.
Пример 1 (см.выше).

Оценки для дисперсии.
Т.к
по определению
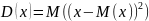 , то
, то

- выборочная (эмпирическая) дисперсия (среднее арифметическое квадратов отклонений от выборочного среднего).
Вычисление
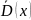 удобно производить
по формуле (аналог D(x)=M(x2
)-(M(x))2):
удобно производить
по формуле (аналог D(x)=M(x2
)-(M(x))2):
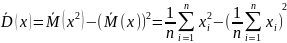
также случайная величина (т.к. зависит от случайных значений выборки), поэтому найдем для нее математическое ожидание:
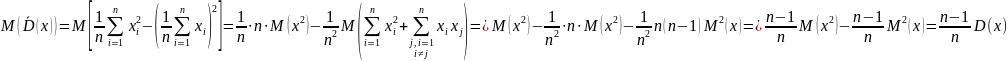
Следовательно, оценка является смещённой. Очевидно, несмещённая оценка дисперсии может быть задана формулой:
 - исправленная
дисперсия,
или
- исправленная
дисперсия,
или
 .
.
Можно показать,
что оценки
и
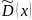 являются состоятельными.
являются состоятельными.
Оценки для среднего квадратического отклонения.
Выборочным средним квадратическим отклонением называется :
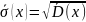
Исправленным средним квадратическим отношением называется :
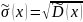
Но оценка
 является всё же смещённой (из несмещённости
является всё же смещённой (из несмещённости
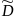 не следует несмещённость
не следует несмещённость
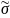 ).
).
Замечание
. Если изучаемая случайная величина
непрерывная с интервальной таблицей
частот, то при вычислении
 ,
,
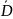 ,
в качестве
,
в качестве
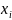 берут середину
интервала
берут середину
интервала
 ,
т.е.
,
т.е.
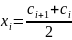 .
.
Оценки для моментов случайной величины.
В качестве оценок начальных и центральных моментов принимают соответствующие выборочные средние значения:
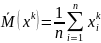 -оценка для начальных
моментов k-порядка;
-оценка для начальных
моментов k-порядка;
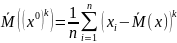 -
оценка для центральных
моментов k-порядка.
-
оценка для центральных
моментов k-порядка.
Статистические оценки начальных моментов являются несмещёнными и состоятельными.
Оценки центральных моментов оказываются состоятельными, но смещёнными.
Замечание. Оценки для математического ожидания, дисперсии, моментов это числовые характеристики выборки. В качестве описательных характеристик вариационного ряда используются мода, медиана, размах вариации и т.д.
Модой
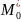 вариационного
ряда называется варианта, имеющая
наибольшую частоту.
вариационного
ряда называется варианта, имеющая
наибольшую частоту.
Медианой
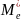 вариационного ряда называется значение,
приходящееся на середину ряда. При этом:
вариационного ряда называется значение,
приходящееся на середину ряда. При этом:
если n=2i+1(нечётное число значений), то
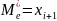 ;
;если n=2i (чётное), то
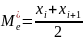 .
.
Размахом вариации R называется разность между наибольшей и наименьшей вариантами.
Пример
1(см.выше).
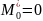 и
и

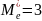 R=6-0=6
R=6-0=6
§4. Методы нахождения оценок.
Метод моментов (К.Пирсон)
Этот метод заключается в том, что определенное количество выборочных моментов (начальных или центральных) приравнивается к соответствующим моментам теоретического распределения, являющимся функциями от неизвестных оцениваемых параметров. Решая полученную систему уравнений относительно этих параметров, находим искомые оценки.
Рассматриваемое количество моментов должно быть равно числу подлежащих оценке параметров.
Этот метод не требует сложных вычислений, он даёт состоятельные оценки, но зачастую малоэффективные.
Пример. Найти по выборке x1; х2;…; xn точечную оценку неизвестного параметра λ показательного распределения.
Решение.
Начальный теоретический момент 1-ого порядка (математическое ожидание):
M(x)
=
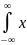 f(x)
dx
=
f(x)
dx
=
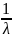
Выборочный начальный момент 1-ого порядка:
(x)
=
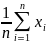 =>
=
=>
=>
=
=>
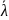 =
=
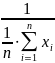 (искомая оценка равна величине, обратной
выборочному среднему).
(искомая оценка равна величине, обратной
выборочному среднему).
Метод максимального правдоподобия
Имеется независимая выборка значений величины X: x1; х2;…; xn.
Предположим, что вид закона распределения X задан, но неизвестен параметр t, от которого зависит этот закон.
В качестве оценки берется функция (функция правдоподобия), которая приводит к наибольшей вероятности появления именно той выборки, которая получена.
Пусть X – дискретная случайная величина.
L(x1; х2;…; xn; t) = p(x1; t)∙ p(x2; t)∙…∙p(xn; t) - функция правдоподобия (где p(xi ,t) - вероятность того, что в результате испытания X= xi).
В качестве оценки принимается такое значение t, при котором функция правдоподобия достигает максимума.
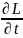 =0 – уравнение
правдоподобия.
=0 – уравнение
правдоподобия.
Замечание. В случае, когда имеется несколько параметров распределения, дифференцируют функцию правдоподобия по каждому из параметров, приравнивают все частные производные к 0 и, решая полученную систему уравнений, находят искомые оценки параметров.
Функции
L
и
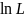 достигают
максимума при одном и том же значении
t,
поэтому рассматривают логарифмическую
функцию правдоподобия:
достигают
максимума при одном и том же значении
t,
поэтому рассматривают логарифмическую
функцию правдоподобия:
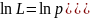 ;
t) +
;
t) +
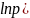 ;
t)+…+
;
t)+…+
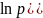 ;
t)
;
t)
Пусть X – непрерывная случайная величина.
L(x1; х2;…; xn; t) = f(x1; t)∙ f(x2; t)∙ …∙ f(xn; t) - функция правдоподобия
(где f(x,t)-плотность вероятности).
Важность метода максимального правдоподобия связана с его оптимальными свойствами. Оценки являются состоятельными, несмещенными. Основной недостаток - трудность вычислений.
Пример. Найти оценку для вероятности p наступления некоторого события A по данному числу m появления этого события в n независимых испытаниях.
Решение.
Составим функцию правдоподобия:
L(x1;
х2;…;
xn;
p)
=
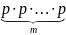
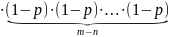 =
=
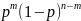
=
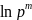 +
+
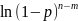 =
m
=
m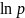 + (n-m)
+ (n-m)
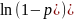 - логарифмическая функция правдоподобия.
- логарифмическая функция правдоподобия.
Уравнение правдоподобия:
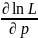 =
=
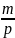 +
+
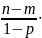 (-1) =
(-1) =
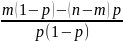 = 0
= 0
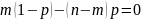
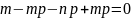
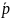 =
=
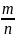 . Оценка
. Оценка
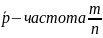 .
.
Метод наименьших квадратов
Оценка определяется из условия минимизации суммы квадратов отклонений выборочных данных от определяемой оценки. Это один из наиболее простых приемов.
Пример.
Над системой (X;Y) произведено n-независимых опытов, в результате которых получены данные: (x1; y1), (х2, у2), …, (хn; уn).
Требуется найти такие a,b, чтобы y=ax+b.
Решение.
Ф
(а; b) =
 2
2

После преобразований можно получить:
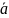 =
=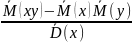
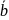 =
(y)
–
(x)
=
(y)
–
(x)
y= x + - эмпирическое (или выборочное) уравнение регрессии Y на X.
Метод наименьших квадратов получил самое широкое применение в практике статистических исследований, так как, во-первых, не требует знания закона распределения выборочных данных, во-вторых, достаточно хорошо разработан в плане вычислительной реализации.
