- •Раздел 14. Элементы математической статистики.
- •§1.Выборка. Обработка результатов.
- •§ 2.Эмпирическая функция распределения.
- •§ 3 Оценки параметров.
- •Оценка для математического ожидания.
- •Оценки для дисперсии.
- •Оценки для среднего квадратического отклонения.
- •Оценки для моментов случайной величины.
- •§4. Методы нахождения оценок.
- •§5. Доверительные интервалы.
- •Доверительный интервал для m при неизвестном σ.
- •§6. Понятие о статистических гипотезах.
§ 2.Эмпирическая функция распределения.
Пусть наблюдается некоторая случайная величина Х. Ее функция распределения F(х) неизвестна. Как с помощью опытных данных получить приближение этой функции?
Пусть n – объем выборки, nx - число наблюдений, при которых полученное значение величины Х меньше x.
Тогда относительная
частота события (X
< x
) равна ![]() .
.
Напомним, что F(х) = P(X < x).
Приближением для вероятности служит частота, поэтому естественно ввести статистический аналог функции распределения

F*(x) =
Функция F*(х) называется эмпирической функцией распределения.
Для дискретного вариационного ряда эмпирическая функция распределения представляет собой разрывную ступенчатую функцию (по аналогии с функцией распределения для дискретной случайной величины).
Пример 1 (см.выше):
0 |
2 |
3 |
4 |
6 |
7/25 |
7/25 |
5/25 |
2/25 |
4/25 |

0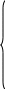 , x
≤ 0
, x
≤ 0
7/25, 0 < x ≤ 2
1![]() 4/25, 2
< x
≤ 3
4/25, 2
< x
≤ 3
19/25, 3 < x ≤ 4
21/25, 4 < x ≤ 6
1, x > 6
Для интервального вариационного ряда имеем лишь значения функции F*(x) на концах интервала. Поэтому для графического изображения этой функции целесообразно ее доопределить, соединив точки графика, соответствующие концам интервалов, отрезками прямой.
Пример 2 (см.выше):
(-20; -15] |
(-15; -10] |
(-10; -5] |
(-5; 0] |
(0; 5] |
(5; 10] |
(10; 15] |
0,08 |
0,11 |
0,18 |
0,26 |
0,19 |
0,12 |
0,06 |
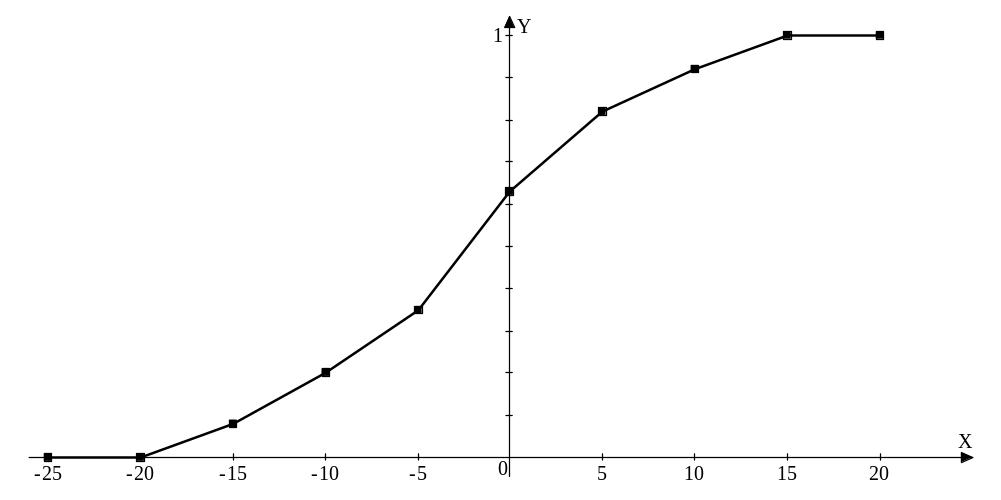
Свойства F*(x):
1) значения F*(x) принадлежат отрезку [0; 1];
2) F*(x) – неубывающая функция;
3) F(x) = 0 при x ≤ λ1 (наименьшего значения);
4) F(x) = 1 при x > λm (наибольшего значения).
§ 3 Оценки параметров.
На практике чаще встречаются ситуации, когда изучаемый закон распределения ясен из каких-либо теоретических соображений.
Остаётся найти некоторые параметры, от которых он зависит. В этом и состоит третий этап обработки выборки (1 этап -составление вариационного ряда, 2 этап - составление эмпирического закона распределения).
Определение приближённых значений параметров распределения случайной величины по выборке называется статистическим оцениванием параметров, а полученные при этом приближённые значения параметров называются статистическими оценками.
Оценка называется точечной, если она представляет собой одно число.
Пусть закон
распределения случайной величины Х
содержит
некоторый параметр t,
численное значение которого неизвестно.
Требуется оценить значение параметра
t,
исходя из значений величины Х,
полученных в результате n
независимых опытов:
 ,
,
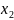 , …,
, …,
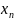 .
.
Любая оценка
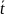 параметра
t
зависит от
,
,…,
,т.е
параметра
t
зависит от
,
,…,
,т.е
= ( ; ; …; )
К оценке предъявляются следующие требования:
М( )=t
В этом случае оценка называется несмещённой. Это требование весьма важно при малом числе опытов.
т.е . случайная величина концентрируется у t. Такую оценку называют состоятельной.