
- •Понятие математической модели.
- •Устойчивость.
- •Типы погрешностей.
- •Приближенные числа. Абсолютные и относительные погрешности.
- •Округление.
- •Погрешности арифметических операций над приближенными числами.
- •Погрешность функции.
- •Представление вещественных чисел.
- •Арифметические операции над числами с плавающей точкой.
- •Вычисление машинной точности.
- •Методы отыскания решений нелинейных уравнений.
- •Система линейных алгебраических уравнений.
- •Вычисление lu-разложения (метод Гаусса).
- •Вычисление luр-разложения (метод Гаусса с выбором ведущего элемента).
- •Система линейных алгебраических уравнений.
- •Метод прогонки.
- •Система линейных алгебраических уравнений.
- •Итерационные методы решения систем линейных алгебраических уравнений.
- •Одномерная минимизация.
- •Методы прямого поиска.
- •Оптимальный пассивный поиск.
- •Постановка задачи приближения функций.
- •Полиномиальная интерполяция. Многочлен Лагранжа.
- •Минимизация погрешности оценки интерполяции. Многочлены Чебышева. Постановка задачи минимизации оценки погрешности.
- •Многочлены Чебышева.
- •Постановка задачи приближения функций. В13
- •16 Глобальные способы построения кубических сплайнов.
- •17 Граничные условия для кубических сплайнов
- •Метод наименьших квадратов.
- •Методы численного дифференцирования. Численное дифференцирование.
- •Устойчивость.
- •Адекватность дискретной модели исходной математической задаче;
- •Сходимость численного решения к точному решению;
- •Устойчивость выбранного метода решения.
- •Численное интегрирование. Формулы прямоугольников и трапеций/Формула Симпсона
- •Методы Монте-Карло.
- •Обыкновенные дифференциальные уравнения. Метод Эйлера.
- •Обыкновенные дифференциальные уравнения.
Вычисление luр-разложения (метод Гаусса с выбором ведущего элемента).
Будем называть элементы, на которые мы делим в процессе построения LU-разложения ведущими. Видно, что они стоят на диагонали матрицы U. Матрица Р соответствует перестановке уравнений, которая предотвращает деление на ноль (или на очень маленькое число) в описанном процессе. Этот прием называется выбором ведущего элемента. Нам дана невырожденная (пп)-матрица А, а построить мы хотим матрицы P, L и U (матрицу перестановки, нижне-треугольную матрицу с единицами на главной диагонали и верхне-треугольную матрицу), для которых PA = LU.
Сначала переместим ненулевой элемент из первого столбца матрицы А – пусть это ak1 в левый верхний угол матрицы. (Если в первом столбце одни нули, матрица вырожденная, а мы предположили, что это не так. Переставим строки 1 и к в матрице А (что соответствует перестановке уравнений, умножив А слева на матрицу перестановки Q. Тогда
![]() ,
,
где v = (а21, а31, …, ак-1,1, а11, ак+1,1, …, ап1)Т (к-й элемент заменен на первый), wT – (ак2, …, акn), и матрица А' имеет размер (п-1) (п-1); теперь ak1 0 и мы можем действовать как для LU-разложения, не опасаясь деления на ноль:
.
Матрица А' – vwТ/ak1 (дополнение Шура) является невырожденной (иначе вторая матрица выписанного разложения имела бы определитель 0, и сама матрица А имела бы определитель 0, что противоречит условию). По индуктивному предположению построим для (п-1) (п-1) матрицы А'–vwТ/ak1 LUP-разложение, найдя нижне-треугольную матрицу L’ с единицами на главной диагонали, верхне-треугольную матрицу U' и матрицу перестановки Р’, для которых
P’(А' – vwТ/ak1) = L’U’.
Рассмотрим матрицу
![]()
Она будет матрицей перестановки (как произведение двух матриц перестановки). Искомым LUP-разложением будет
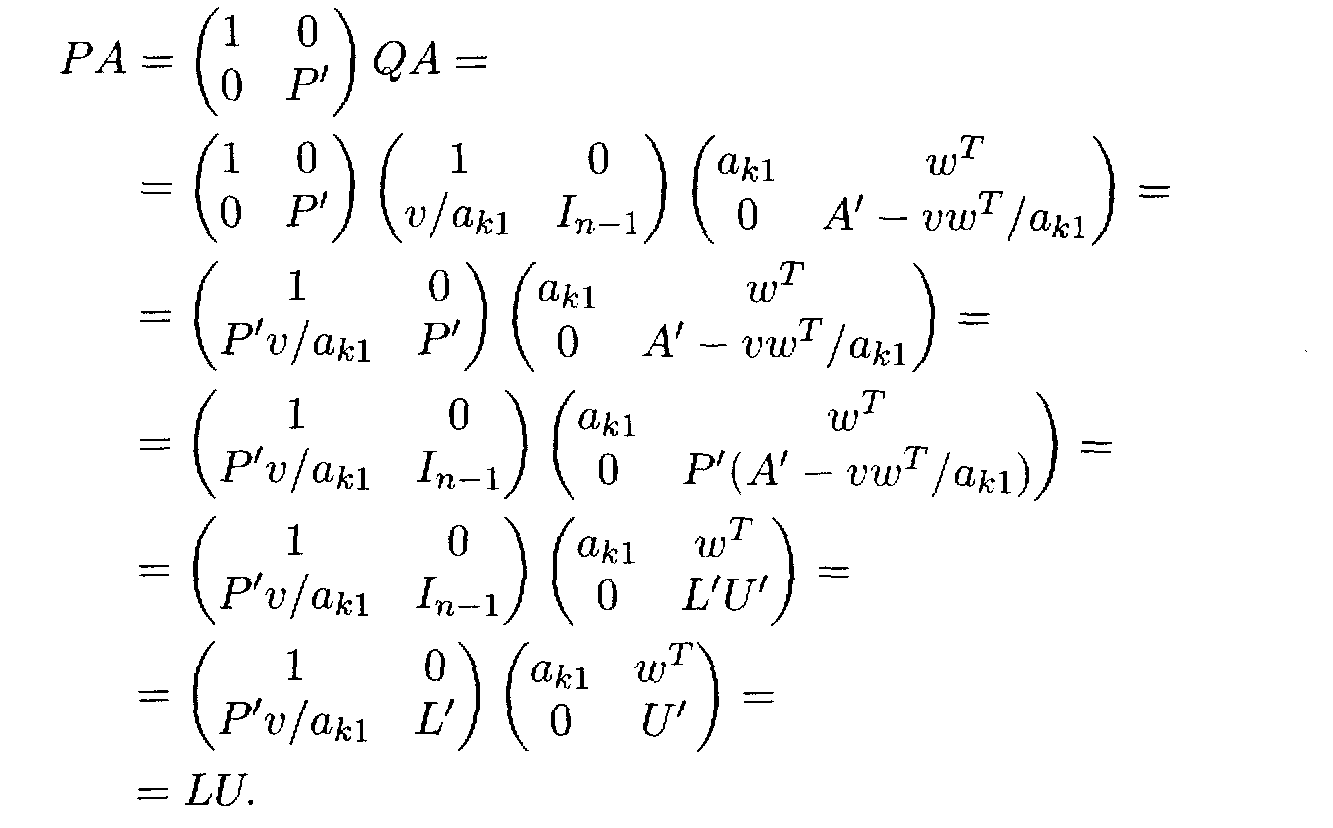
Матрица L’ - нижне-треугольная с единицами на главной диагонали, a U' – верхне-треугольная, и потому матрицы L и U также обладают этим свойством.
Отличие от аналогичных формул для LU-разложения состоит в том, что вектор-столбец v/ak1 и дополнение Шура А' – vwТ/ak1 умножаются на матрицу перестановки Р'.
10
Система линейных алгебраических уравнений.
Рассмотрим систему линейных уравнений с постоянными коэффициентами:
а11х1 + а12х2 + а13х3 + … + а1тхт = b1,
а21х1 + а22х2 + а23х3 + … + а2тхт = b2,
а31х1 + а32х2 + а33х3 + … + а3тхт = b3,
………………………………………….
аm1х1 + аm2х2 + аm3х3 + … + аmтхт = bm .
В матричной форме записи эта система принимает вид Ax = b, где
, , .
Будем предполагать, что матрица А задана и является невырожденной. Известно, что в этом случае решение системы существует, единственно и устойчиво к входным данным, т.е. рассматриваемая задача является корректной.
Метод прогонки.
Метод прогонки является простым и эффективным алгоритмом решения систем линейных алгебраических уравнений с трехдиагональными матрицами:
b1x1 + c1x2 = d1 ,
a2x1+b2x2+c2x3 = d2 ,
…………………………………………………
(21)
aixi-1+bixi+cixi+1 = di ,
…………………………………………
am-1xm-2+bm-1xm-1+cm-1xm = dm-1 ,
amxm-1+bmxm = dm .
Системы такого рода часто возникают при решении различных задач математической физики, а также при решении других вычислительных задач (например, приближения функций сплайнами).
Вывод расчетных формул.
Преобразуем первое уравнение системы (21) к виду
x1=1x2+1 ,
где 1= -с1 / b1 , 1 = d1 /b1.
Подставим полученное для х1 выражение во второе уравнение системы:
a2(1x2 +1) + b2x2 + c2x3 = d2 .
Преобразуем это уравнение к виду:
x2 = 2x3 + 2 , (22)
где 2 с2 /b2 1 , d2 21 /b2a21 .
Выражение (22) подставляем в третье уравнение системы и т.д.
На i - м шаге этого процесса получаем (1< i < m) i-е уравнение системы преобразуется к виду
xi = ixi+1 + i , (23)
где i = -ci /(bi + aii) , i = (di - aii)/(bi+aii-1) .
На т-м шаге подстановка в последнее уравнение выражения xm-1 = m-1xm + m-1 дает
mm-1xm + m-1 + bmxm = dm .
Отсюда
xm = m = (dm - amm-1)/(bm + amm-1) .
Значения остальных неизвестных теперь легко вычисляются по формуле (23).
Алгоритм прогонки.
Сделанные преобразования позволяют организовать вычисления метода прогонки в два этапа.
Прямой ход метода прогонки (прямая прогонка) состоит в вычислении прогоночных коэффициентов i (1 i<m) и i (1 i<m) . При i=1 коэффициенты вычисляются по формулам
1 -с11 1 d1 1 1 = b1,
а при i = 2, 3, … , m-1 - по рекуррентным формулам
i -сi i i ( di- aii-1) i i = bi + aii-1 .
При i = m прямая прогонка завершается вычислением
m ( dm - amm-1) m m = bm + amm-1 .
Обратный ход метода прогонки (обратная прогонка ) дает значения неизвестных. Сначала полагают хт = т. Затем значения остальных неизвестных вычисляются по формуле
хi = ixi+1 + i , i = m-1, m -2,… , 1.
Вычисления ведут в порядке убывания значений i от т - 1 до 1.
Непосредственный подсчет показывает, что для реализации вычислений требуется примерно 8т арифметических операций. Кроме того, трехдиагональная структура матрицы системы позволяет использовать для ее хранения лишь 3т - 2 машинных слова.
Таким образом, при одной и той же производительности и оперативной памяти ЭВМ метод прогонки позволяет решать системы гораздо большей размерности, чем стандартный метод Гаусса для систем уравнений с заполненной матрицей.
Достаточными условиями на коэффициенты прогонки, при которых решение системы является корректной задачей, являются
bkakck bkak (1 k m) .
11
