16 Глобальные способы построения кубических сплайнов.

Для того, чтобы сплайн S₃(x) имел непрерывную на отрезке [a; b] вторую производную S₃''(x) , необходимо выбирать наклоны s_i так, чтобы в точках х_i "стыка многочленов" Р_{3, i} и P_{3, i+1} совпадали значения их вторых производных:

P''_{3, i}(x_i) = P ''_{3, i+1}(x_i), i = 1, 2, … , n - 1.

Пользуясь формулой (32), найдем значение

. (33')

Из подобной формулы, записанной для многочлена P_{3, i+1}, имеем

. (33'')

Таким образом, получаем следующую систему уравнений относительно коэффициентов s_i:

(34)

Заметим, что эта система недоопределена, т.к. число уравнений системы (равное п - 1) меньше числа неизвестных (равного п+1). Выбор двух оставшихся уравнений обычно связывают с некоторыми дополнительными условиями, накладываемыми на сплайн в граничных точках а и b (граничными условиями). Укажем на некоторые из наиболее известных граничных условий:

17 Граничные условия для кубических сплайнов

1. Если в граничных точках известны значения первой производной f '(a) и f '(b), то естественно принять

s₀ = f '(a), s_n = f '(b) . (35)

Дополняя систему (34) уравнениями (35), приходим к системе уравнений с трехдиагональной матрицей, которая легко решается методом прогонки. Полученный таким образом сплайн называется фундаментальным кубическим сплайном.

2. Если в граничных точках известны значения второй производной f ''(a) и f ''(b), то можно наложить на сплайн граничные условия S₃''(a) = P_3,1^''(a) = f ''(a), S₃''(b) = P_3,n^''(x_n) = f ''(b), что приводит к следующим уравнениям:

(36')

(36'')

(достаточно в равенстве (33'') взять i = 0 , а в равенстве (33') i=n ).

3. Полагая в уравнениях (36'), (36'') f ''(a) = f ''(b) =0 (независимо от того, выполнены ли эти условия для интерполируемой функции), придем к системе уравнений, определяющий так называемый естественный кубический сплайн.

4. Часто нет никакой дополнительной информации о значениях производных на концах отрезка. Один из применяемых в этой ситуации подходов состоит в использовании условия "отсутствия узла". Выбор наклонов s_i производят таким образом, чтобы для получаемого сплайна выполнялось условие P_3,1(x)  P_3,2(x), P_3,n-1(x)  P_3,n(x). Для этого достаточно потребовать совпадения в точках х₁, х_п-1 соответствующих третьих производных:

P⁽³⁾_3,1(x₁)  P⁽³⁾_3,2(x₁), P⁽³⁾_3,n-1(x_п-1)  P⁽³⁾_3,n(x_п-1) .

Эквивалентные алгебраические уравнения выглядят так:

2h₁^-3(y₀ - y₁) + h₁^-2(s₀ + s₁) = 2h₂^-3(y₁ - y₂) + h₂^-2(s₁ + s₂),

2h_n-1^-3(y_n-2 - y_n-1) + h_n-1^-2(s_n-2 + s_n-1) = 2h_n^-3(y_n-1 - y_n) + h_n^-2(s_n-1 + s_n).

5. Если f - периодическая функция с периодом, равным b-a , то систему (34) следует дополнить условиями

s₀ = s_n ,

h_n^-1(s_n-1 + 2s_n) + h₁^-1(2s₀ + s₁) = 3[h_n^-2(y_n - y_n-1) + h₁^-2(y₁ - y₀)]

18-19

Метод наименьших квадратов.

Пусть функция y=f(x) задана таблицей приближенных значений

y_i  f (x_i), i = 0, 1, … , n,

полученных с ошибками _i = y_i⁰ - y_i, где y_i⁰ = f (x_i). Если значения y_i получены из эксперимента, то ошибки носят случайный характер и уровень погрешности ("шума" таблицы) может быть значительным.

Предположим, что для аппроксимации функции f используется линейная модель:

у = (х)  а₀₀(х)  а₁₁(х)    а_т_т(х) .

Здесь ₀(х), ₁(х),  , _т(х) - заданные базисные функции, а₀, а₁, , а_т - параметры модели. Одной из самых простых и часто используемых моделей является полиномиальная модель

у = Р_т(х)  а₀  а₁х    а_тх^т .

В случае, когда уровень неопределенности исходных данных высок, нецелесообразно использовать интерполяцию, поскольку при интерполировании происходит повторение ошибок наблюдений, в то время как при обработке экспериментальных данных, напротив, желательно их сглаживание. Однако следует все же стремиться к тому, чтобы выполнялись приближенные равенства

а₀₀(х₀)  а₁₁(х₀)    а_т_т(х₀)  у₀,

а₀₀(х₁)  а₁₁(х₁)    а_т_т(х₁)  у₁,

………………………………………..

а₀₀(х_n)  а₁₁(х_n)    а_т_т(х_n)  у_n ,

или в матричном виде Ра  у .

Из различных критериев, позволяющих выбрать параметры модели а₀, а₁, , а_т так, чтобы данные приближенные равенства выполнялись наилучшим в некотором смысле образом, наиболее часто используется критерий наименьших квадратов. Согласно этому критерию параметры выбираются так, чтобы минимизировать среднеквадратичное уклонение

.

Здесь . Заметим, что минимум среднеквадратичного уклонения достигается при тех же значениях а₀, а₁, , а_т , что и минимум функции

.

Простейший подход к решению поставленной задачи состоит в использовании необходимого условия экстремума функции s:

Если система функций ₀(х), ₁(х),  , _т(х) линейно независима в точках х₀, х₁, … , х_п , то многочлен наилучшего среднеквадратичного приближения существует и является единственным. В случае приближения алгебраическими многочленами получаем систему уравнений

(3)

Запишем систему (3) в развернутом виде в двух наиболее простых случаях т = 1 и т = 2. Для многочлена первой степени Р₁(х) = а₀ + а₁х получаем

18

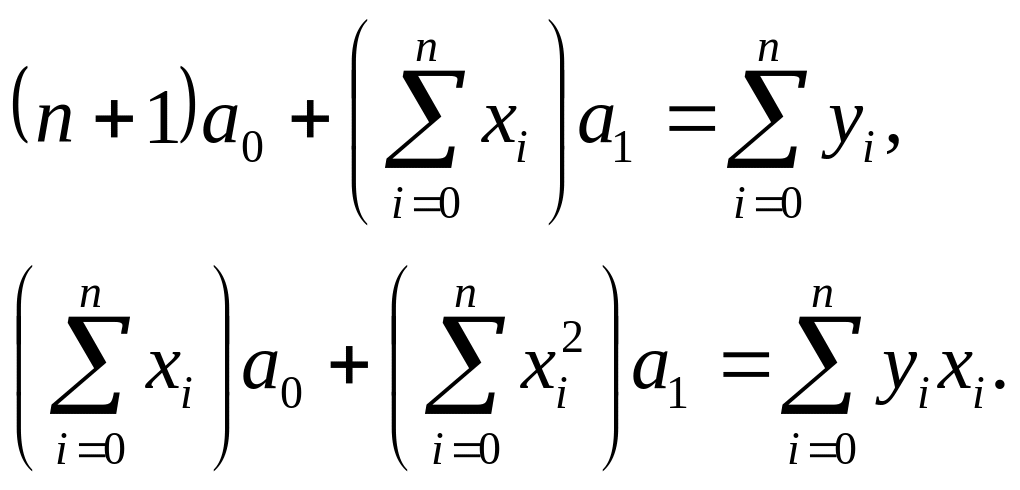
Если же используется многочлен второй степени Р₂(х) = а₀ + а₁х + а₂х², то имеем

19

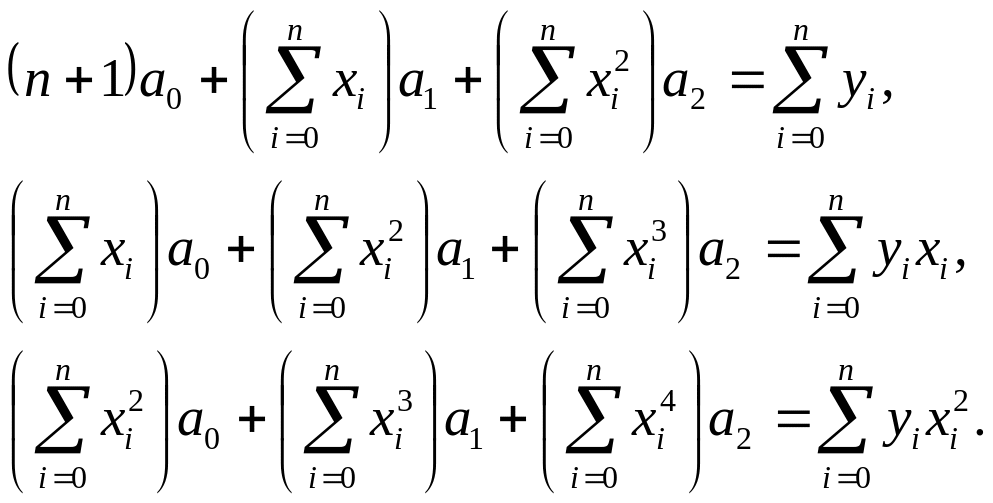
Систему (3) из п уравнений можно записать как матричное уравнение

(Ас - у)^ТА = 0,

которое эквивалентно уравнению А^Т(Ас-у) = 0.

Раскрыв скобки, мы приходим к уравнению

А^ТАс = А^Ту, (4)

называемому в математической статистике нормальным уравнением. Матрица АТА будет симметрической, и, если только А имеет полный столбцовый ранг, положительно определенной. В этом случае существует обратная матрица (АТА)-1 , и решение системы (4) единственно:

с = ((А^ТА)^-1А^Т)у = А⁺у .

Здесь через А⁺ обозначена матрица (А^ТА)^-1А^Т, называемая псевдообратной к матрице А. Это понятие является естественным обобщением понятия обратной матрицы на случай неквадратных матриц.

20