Методы Монте-Карло.
В качестве примера рассмотрим вычисление интегралов методом Монте-Карло. Хотя основное преимущество данных методов проявляется при вычислении многомерных интегралов, основные идеи метода рассмотрим на одномерной задаче.
Пусть требуется вычислить интеграл
.
Будем рассматривать этот интеграл как среднее значение функции f на отрезке [0, 1]. При таком подходе соответствующая квадратурная формула запишется в виде
.
В этой формуле среднее значение f вычисляется усреднением ее N значений при значениях абсцисс {xi}, равномерно распределенных на отрезке [0, 1].
Для оценки погрешности полученной формулы интегрирования мы можем рассматривать fi = f (xi) как случайную величину и при больших N, согласно законам статистики, получаем:
.
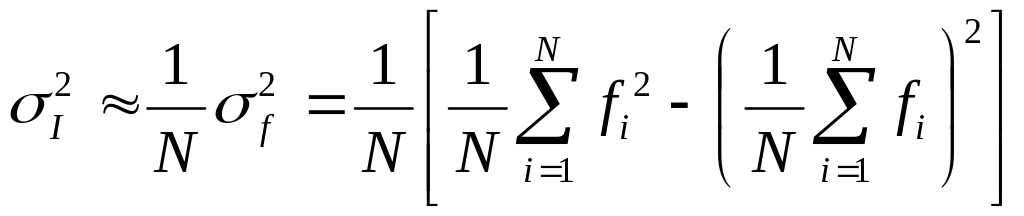При увеличении числа точек точность вычисления интеграла увеличивается, хотя и очень медленно (для уменьшения ошибки в 2 раза объем вычислений увеличивается в 4 раза).
Пример
вычисления двумерного интеграла
методом Монте-Карло Пусть f
равна нулю везде, за исключением очень
узкого пика в окрестности некоторой
точки х.
Если выбирать случайные абсциссы хi,
равномерно распределенные на отрезке
[0, 1], то очень вероятно, что большинство
точек будет давать значения функции,
близкие к нулю. В этом случае оценка
интеграла будет плохой.
Для повышения эффективности метода умножим и разделим подынтегральную функцию на положительную весовую функцию (х), нормированную условием
.
В результате искомый интеграл запишется в виде
.
После замены переменной х на
получаем
(поскольку
, у(0)
= 0, у(1)
= 1)
.
Оценка этого интеграла методом Монте-Карло проводится так же, как это было сделано выше, усреднением значений f/ по случайной выборке точек у, равномерно распределенных на интервале [0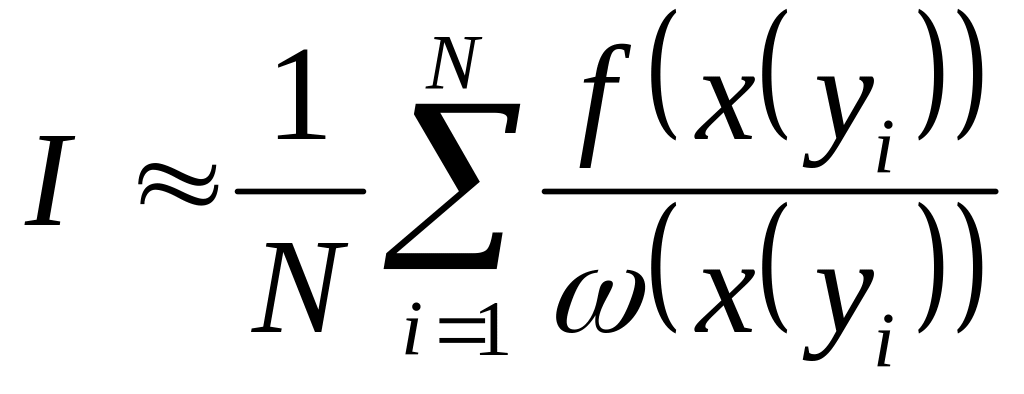, 1]:
. (1)
Если мы выберем такую функцию , которая ведет себя так же, как и f, то подынтегральная функция f/ может быть сделана очень слабо меняющейся, что приводит к уменьшению дисперсии в оценке интеграла методом Монте-Карло.
Пример.
Рассмотрим интеграл
.
Хорошим выбором для весовой функции будет функция
,
которая положительна и монотонно падает на отрезке интегрирования (так же, как f ) и нормирована на 1. Новая переменная интегрирования будет равна
,
откуда можно выразить обратную функцию
.
Теперь можно вычислить интеграл по формуле (1).
25
Обыкновенные дифференциальные уравнения. Метод Эйлера.
Многие из законов природы наиболее удобно формулировать в виде дифференциальных уравнений.
Обыкновенное дифференциальное уравнение самого общего вида можно свести к системе М дифференциальных уравнений
,
где
х
– независимая переменная, а
и
- М
–компонентные
вектора.
Основой для решения обыкновенных дифференциальных уравнений первого порядка является задача Коши:
(1)
с одной зависимой переменной y(x) на интервале [a ; b] и задано у(а)=у2.
Интервал, на котором рассматривается решение, разбивается на большое число N одинаковых отрезков длиной h = (b-a) / N , в каждой точке которого ищется приближенное решение yn .
Метод
Эйлера. В
уравнении (1) производная заменяется
ее конечно-разностным значением: 
(2)
Отсюда получается рекуррентная формула
yn+1 = yn + hf(xn,yn) + O(h2) .
Метод Эйлера имеет низкий порядок точности. Класс простых методов более высокого порядка можно получить из разложения yn+1 вблизи yn в ряд Тейлора:
Поскольку
,
[x0,a]
,
получим
(3)
Точность полученной формулы на порядок превышает точность формулы Эйлера.
26-27