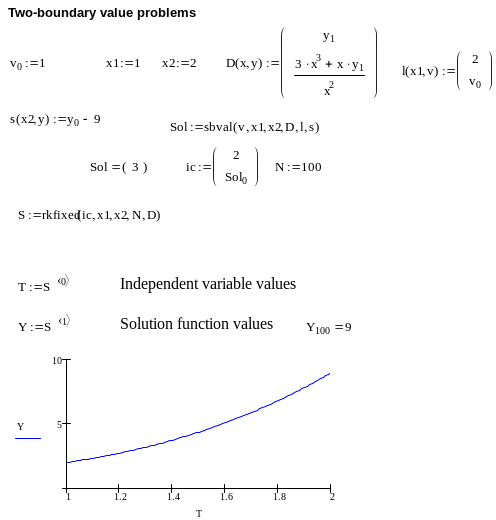Обыкновенные дифференциальные уравнения.
Многие из законов природы наиболее удобно формулировать в виде дифференциальных уравнений.
Обыкновенное дифференциальное уравнение самого общего вида можно свести к системе М дифференциальных уравнений
,
где х – независимая переменная, а и - М –компонентные вектора.
Основой для решения обыкновенных дифференциальных уравнений первого порядка является задача Коши:
(1)
с одной зависимой переменной y(x) на интервале [a ; b] и задано у(а)=у2.
Интервал, на котором рассматривается решение, разбивается на большое число N одинаковых отрезков длиной h = (b-a) / N , в каждой точке которого ищется приближенное решение yn .
26-27 Многошаговые и неявные методы.
(42)
Рассмотрим уравнение (42). Проинтегрируем его точно на одном шаге:
(44)
Значение функции на отрезке интегрирования будем приближенно рассчитывать методом линейной экстраполяции:
(45)
Здесь fi f(xi,yi) .
Подставляя (45) в (44) и интегрируя, получим схему двухшагового метода Адамса-Бэшфорта:
Если исходную функцию экстраполировать кубическим полиномом, получим
4-
шаговый
метод Адамса-Бэшфорта: 
Рассмотренные методы относятся к явным в том смысле, что yn+1 выражается в виде явной зависимости от других известных значений yn.
Рассмотрим уравнение (42) в точке, расположенной посредине между узлами сетки:
(46)
Воспользовавшись симметричной разностной аппроксимацией производной с шагом h/2, а также заменяя f n+1/2 его средним арифметическим по значениям f в соседних узлах сетки, получим
Отсюда получаем рекуррентное соотношение
(47)
Мы видим, что уравнение (47) имеет неявный вид, т.к. yn+1 содержится в обеих частях уравнения. Решение такого уравнения требует более нетривиальных методов решения по сравнению с явными методами.
27 Методы Рунге-Кутты. (1)
Рассмотрим уравнение (1). Проинтегрируем его точно на одном шаге:
(4)
Аппроксимируем функцию в уравнении (4) первыми членами ее разложения в ряд Тейлора в средней точке отрезка интегрирования. Тогда (поскольку интеграл от линейного члена равен 0)
Определим величину к как некоторое приближение в два раза больше разности между yn+1/2 и yn . Тогда
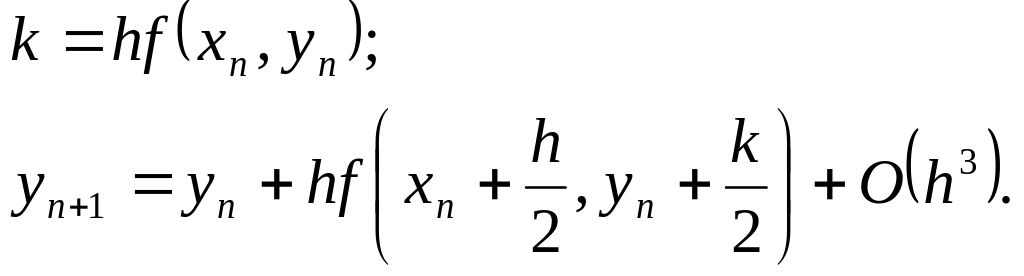
Таким образом мы получили формулы Рунге-Кутты второго порядка. Суть этого метода заключается в подстановке некоторых приближенных значений у в неявные выражения, содержащие f в правой части. Точность этого метода такая же, как у Тейлоровского разложения, однако здесь отсутствуют ограничения на вид f (например, легкая дифференцируемость, линейность по у и т.п.).
Подобным образом выводятся и формулы Рунге-Кутты более высоких порядков точности. Интеграл (4) аппроксимируется конечной суммой нескольких значений f , используя любые квадратурные формулы, например, формулу Симпсона, и с соответствующей точностью аппроксимируются значения у, входящие в правую часть полученного соотношения. Опытным путем найдено, что наилучшее соотношение точности расчетов и объема необходимых вычислений достигается в схеме Рунге-Кутты четвертого порядка (т.е. требующую четырех вычислений значений f на каждом шаге интегрирования):
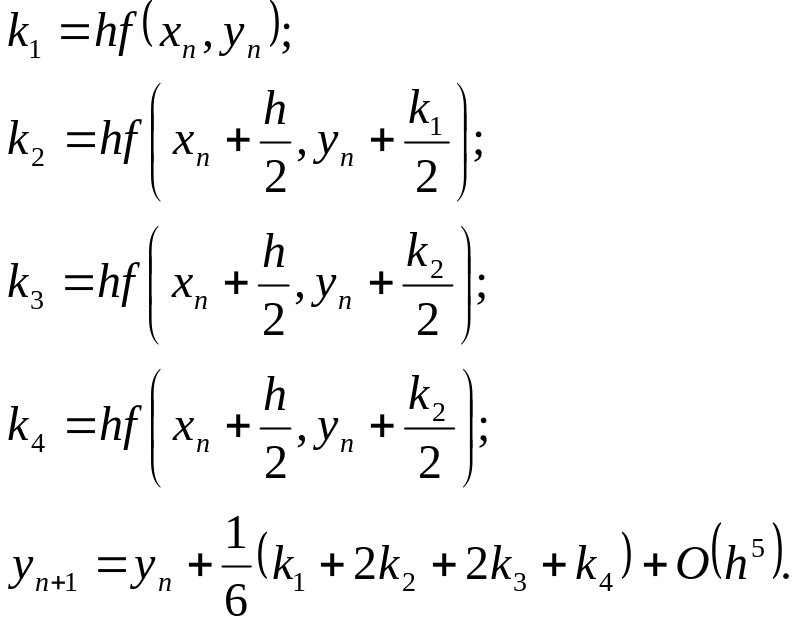(5)
Для решения задачи Коши в MathCad имеются опции odesolve, rkfixed, Bulstoer, Stiffb, Stiffr, Radau и Rkadapt. Последние четыре опции применяются для решения жестких уравнений и систем. Наиболее часто применяются опции odesolve и rkfixed.
Опция rkfixed(y, x1, x2, npoints, D) для решения систем дифференциальных уравнений 1-го порядка методом Рунге-Кутты четвертого порядка может использоваться для решения как одного уравнения, так и системы дифференциальных уравнений. Здесь у- вектор начальных условий; х1, х2 – начальная и конечная точки отрезка, на котором ищется решение; npoints – число точек отрезка (за исключением начальной точки), в которых ищется решение; D – векторная функция для вычисления производных.
28
Двухточечные краевые задачи. Одним из распространенных способов решения двухточечных краевых задач (когда дополнительные условия на решение налагаются в точках на концах отрезка), в том числе нелинейных, является метод стрельбы.
При решении задачи методом стрельбы краевая задача сводится к решению задачи Коши, причем недостающие начальные значения задаются вектором параметров, значения которых и находятся «пристрелкой». В MathCad для того, чтобы найти этот вектор, имеется опция sbval(v,x1,x2,D,l,s) и bvalfit(v,x1,x2,xf,D,l1,l2,s). Здесь v – вектор «недостающих» начальных условий; х1,х2 – начальная и конечная точки отрезка, на котором ищется решение; D – вектор производных; l – векторная функция начальных значений; «недостающие» начальные значения задаются компонентами вектора v; s – вектор разностей между вычисленными и точными значениями функций на конце отрезка. Опция bvalfit решает двухточечную краевую задачу, используя промежуточную точку xf интервала решения. Применение этого метода будет особенно успешным, когда производная имеет разрыв внутри отрезка интегрирования.
В качестве примера рассмотрим применение функции sbval для решения краевой задачи х2у'' - xy' = 3x3;
y(1) = 2; y(2) = 9.
Для того, чтобы привести данную задачу к задаче Коши, нам необходимо значение y’(0). Таким образом, вектор v будет иметь одно значение, которое задается произвольно (например, v0=1). Дополнительные условия на решение заданы в точках х1=1, х2=2. Поскольку порядок дифференциального уравнения равен 2, вектор производных содержит две компоненты – у0 и у1, причем выражение для старшей производной находится из дифференциального уравнения. Вектор l содержит начальное значение у, равное 2, и начальное значение y’, которое задано значением v0. Так как на конце отрезка задано только одно значение y(2)=9, s задается скалярной величиной у0-9 (вектор у содержит значение функции у0 и значения производных y1 (y’), y2 (y’’) и т.д.
После определения недостающих начальных условий можно решать задачу Коши, используя какую-либо подходящую опцию (например, rkfixed).
Листинг программы:
