Устойчивость.

В процессе решения задач математического моделирования возникают три основных проблемы:

4. Адекватность дискретной модели исходной математической задаче;

5. Сходимость численного решения к точному решению;

6. Устойчивость выбранного метода решения.

Вопрос устойчивости связан со степенью нарастания в ходе расчета ошибок округления и других ошибок, связанных с проводимыми вычислениями, что во многих случаях может привести к полному искажению результата.

Пример.

Заменим производную в уравнении (42) ее симметричной разностной аппроксимацией. В результате получится рекуррентная формула

(49)

Будем этим методом искать решение задачи

(50)

точное решение которой равно

Использовав разложение искомой функции в ряд Тейлора с точностью до квадратичных членов, получим

Расчет по формуле (49) показывает, что при малых х численное решение в пределах погрешности хорошо согласуется с точным. Затем вблизи х3.5 в численном решении развиваются осцилляции, размах которых нарастает, в конечном счете полностью подавляя ожидаемый экспоненциальный спад для y(x). Данное поведение является признаком неустойчивости применяемого алгоритма.Чтобы понять причину этой неустойчивости, перепишем уравнение (49) в виде

y_n+1 = y_n-1 - 2y_n . (51)

Будем искать решение уравнения (51) в виде , где A,r - некоторые константы. Подставляя в (51), получаем уравнение для r:

Двумя корнями полученного уравнения являются значения

Отрицательному корню соответствует решение

 ,

изменяющее знак при каждом переходе к следующему узлу сетки. Из-за ошибок округления некоторая часть этого решения будет постоянно вноситься в общее решение исходного уравнения, и в конце концов побочное решение станет доминировать.

Особое внимание на проблему устойчивости следует обратить в задачах, где ожидаются строго убывающие решения.

22-23

Численное интегрирование. Формулы прямоугольников и трапеций/Формула Симпсона

В прикладных исследованиях часто возникает необходимость вычисления значения определенного интеграла

.

Рассмотрим формулы интегрирования , которые относятся к классу формул Ньютона-Котеса замкнутого типа. Основная идея, лежащая в основе вывода этих формул заключается в следующем: отрезок, на котором проводится интегрирование, разбивается на равных отрезков и на каждом отрезке исходная функция заменяется приближенной функцией, которая может быть точно проинтегрирована.

Для линейного приближения получаем элементарную квадратурную формулу трапеций:

с точностью О(h²).

Для составной квадратурной формулы трапеций получаем

.

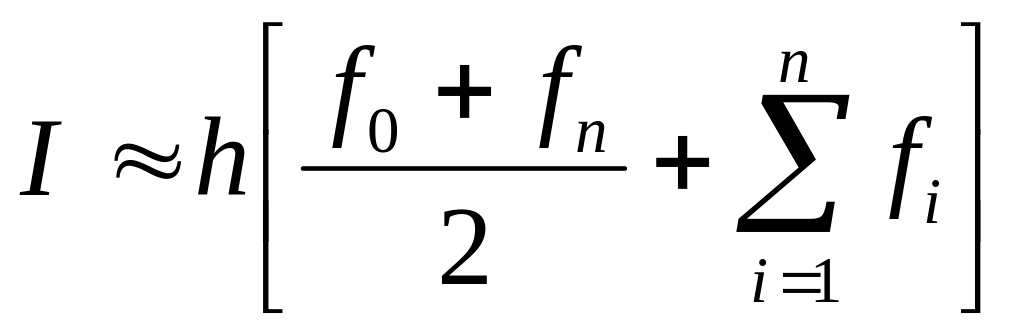Заменяя элементарные криволинейные трапеции прямоугольниками, получаем формулу прямоугольников

.

23 Интегрируя, получаем (формула Симпсона, или формула парабол):

f(x) в ряд Тейлора

Точность интегрирования оказалась больше ожидаемой за счет того, что член разложения ~x³ не дает вклада в интеграл.

Для полного интеграла по формуле Симпсона получаем

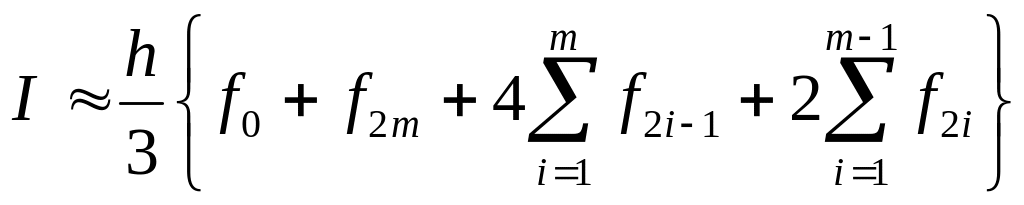
В интегралах, где верхний предел очень велик, полезно сделать замену переменной интегрирования x = t^-1. Соответствующую замену переменных нужно делать в интегралах, где имеется интегрируемая особенность.

24