Погрешность функции.

Пусть f(x) = f(x₁,x₂,…,x_m) – дифференцируемая в области G функция т переменных, вычисление которой производится при приближенно заданных значениях аргументов х₁*, х₂*,…,х_т*. Такая ситуация возникает например, всякий раз, когда на ЭВМ производится расчет по формуле. Важно знать, какова величина неустранимой ошибки, вызванной тем, что вместо значения y = f(x) в действительности вычисляется значение y* = f(x*).

Введем определение отрезка в т-мерном пространстве. Отрезком, соединяющим точки х и х* в т-мерном пространстве называется множество точек вида

х+(1-)х*,    .Пусть [х,х*] – отрезок, соединяющий точки х и х*, и

.

Теорема Для абсолютной погрешности значения у* = f(x*) справедлива следующая оценка:

. (11)

Доказательство.

Рассматриваемая оценка вытекает из формулы конечных приращений Лагранжа:

.

Следствие.

Если х*  х, то в силу оценки (11) можно положить

Равенство (12') удобно для практических оценок, а равенством (12'') удобно пользоваться для теоретических рассмотрений.

Из формул (12') и (12'') вытекают приближенные равенства для оценки границ относительных погрешностей:

.

Здесь

. (13)

Погрешность неявной функции.

Нередко приходится сталкиваться с ситуацией, когда функция y = f(x₁, x₂,…, x_m) задается не явной формулой, а как решение нелинейного уравнения

F(y,x₁, x₂,…, x_m) = 0, т.е. неявно. Если для такой неявной функции воспользоваться известными формулами вычисления производных

то исследование неустранимой погрешности неявной функции сводится к рассмотренному выше случаю.

Пример

Найти абсолютную и относительную погрешность площади круга R=12

%

6

Представление вещественных чисел.

В большинстве современных ЭВМ для вещественных чисел принята форма представления с плавающей точкой, когда каждое число представляют в виде

х =  (₁2^-1  ₂^-2    _t^-t ^p . (15)

Здесь ₁, ₂, … , _t – двоичные цифры. Число х нормализуется так, чтобы ₁ равнялось 1, и поэтому в памяти ЭВМ хранятся только значащие цифры. Число  =  (₁2^-1  ₂^-2    _t^-t называется мантиссой числа х . Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы. Разрядность мантиссы зависит от конструктивных особенностей конкретной вычислительной машины, но всегда является конечной. В представлении (15) р – целое число, называемое двоичным порядком. Порядок также записывают как двоичное целое число р =  _l _l-1  ₀₂ , для хранения которого в машинном слове отводится l + 2 двоичных разрядов. Схематически структуру машинного слова для хранения вещественного числа можно представить следующим образом:

мантисса двоичный порядок

Пример. Представим число х = 20.5 в двоичной системе счисления в нормализованной форме с плавающей точкой. Так как х = (10100.1)₂, то, перемещая двоичную точку на 5 позиций влево, получаем х = (0.101001)2⁵.

На основании имеющихся сведений о представлении чисел в ЭВМ можно сделать следующие выводы:

1. На ЭВМ представимы не все числа, а лишь конечный набор рациональных чисел специального вида. Эти числа образуют представимое множество вычислительной машины. Для всех остальных чисел возможно лишь их приближенное представление с ошибкой, которую принято называть ошибкой представления (или ошибкой округления). Обычно приближенное представление числа х в ЭВМ обозначают как х* = fl(x). Если округление производят по дополнению, то граница относительной погрешности представления равна единице первого отброшенного разряда мантиссы, т.е. 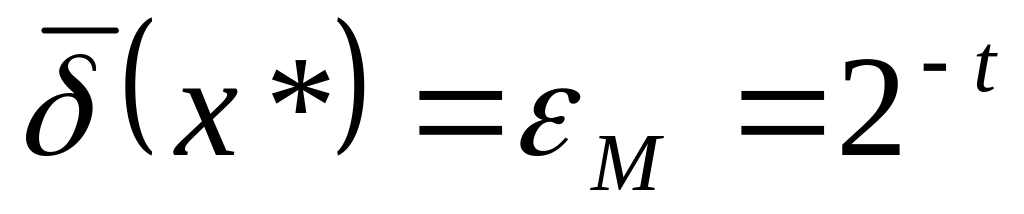(порядок числа не влияет на относительную погрешность представления). Если же округление производят усечением, то 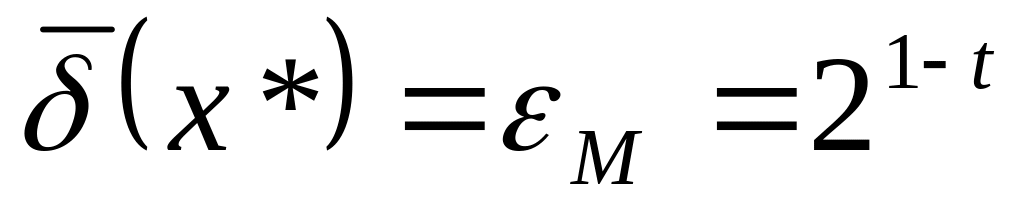. Величину _М называют относительной точностью ЭВМ, а также машинной точностью. Значение этой величины определяется разрядностью мантиссы и способом округления.

Как правило, в представимом множестве ЭВМ нет числа у, являющегося решением поставленной задачи, и лучшее, что можно попытаться сделать – это найти его представление у* = fl(у) с относительной точностью порядка _М.

Например, среди представимых на ЭВМ чисел нет такого широко используемого в вычислениях числа как 0.1. Дело в том, что двоичная запись числа 0.1 является бесконечной периодической дробью: 0.1 = (0.0001100110011…)₂. Поэтому это число всегда представляется на ЭВМ приближенно с погрешностью, вызванной необходимостью округления.

2. Диапазон изменения чисел в ЭВМ ограничен. Так как ₁=1, то для мантиссы  справедливы оценки 0.5   1. В то же время для представления в ЭВМ порядка р используется конечное число ( l + 1) двоичных цифр и поэтому р р_max = 2^{l +1} – 1. Таким образом, для всех представимых на ЭВМ чисел х (за исключением нуля) имеем 0 < X₀  x< X_ , где 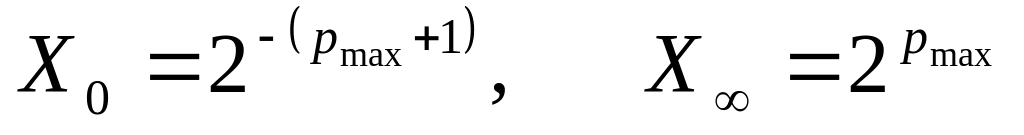. Заметим, что диапазон представления чисел на ЭВМ полностью определяется разрядностью порядка.

3. Все числа х, по модулю большие Х_ , не представимы на ЭВМ и могут рассматриваться как машинная бесконечность. Попытка получить такое число приводит к аварийному останову ЭВМ по переполнению. Все числа х, по модулю меньшие Х₀, для вычислительной машины не различимы и представляются как нуль (машинный нуль). Получение числа х, такого что х<Х₀, называют исчезновением порядка (или антипереполнением). Обычно при исчезновении порядка автоматически полагается fl(x) = 0 и вычисления продолжаются.

Не следует смешивать машинную точность М с минимальным положительным представимым на ЭВМ числом Х0. Это совершенно разные числа, причем Х0 << M.

4. На машинной числовой оси числа расположены неравномерно. Плотность их возрастает по мере приближения к нулю и падает с удалением от нуля. Чтобы убедиться в этом, заметим, что расстояние от одного представимого на ЭВМ числа х до другого ближайшего представимого равно единице последнего разряда мантиссы, умноженной на 2^р, т.е. равно 2^p-t. Так как t фиксировано, то расстояние уменьшается с уменьшением порядка р и возрастает с увеличением р.

7