Полиномиальная интерполяция. Многочлен Лагранжа.

Для заданной таблицы (27) многочлен степени п называется интерполяционным многочленом, если он удовлетворяет условиям

Р_п(х_i) = y_i (i = 0, 1, … , n) . (28)

Данное равенство можно записать в виде системы уравнений

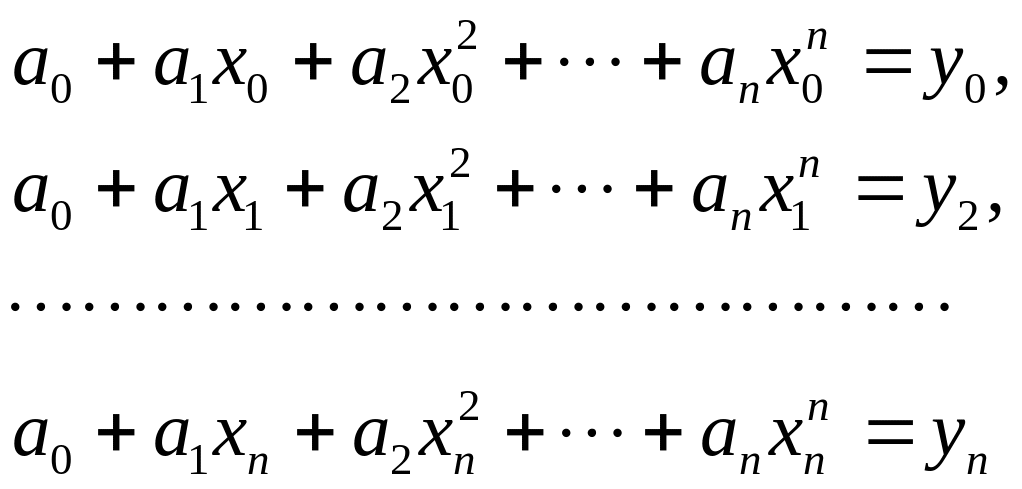(29)

относительно коэффициентов многочлена.

Определитель этой системы, называемый определителем Вандермонда,

отличен от нуля, если узлы интерполяции попарно различны. Следовательно, существует единственный интерполяционный многочлен степени п, удовлетворяющий условиям (28).

На практике система (29) никогда не используется для вычисления коэффициентов интерполяционного многочлена. Дело в том, что часто она является плохо обусловленной, когда малые погрешности округления приводят к большим вычислительным погрешностям. кроме того, существуют различные удобные явные формы записи интерполяционного многочлена, которые и применяются при интерполяции. Наконец, в большинстве приложений интерполяционного многочлена явное выражение коэффициентов a_k не нужно.

Приведем одну из форм записи интерполяционного многочлена - многочлен Лагранжа . Здесь .

Как нетрудно видеть, l_nj(x) представляет собой многочлен степени п, удовлетворяющий условию

Поэтому многочлен Лагранжа действительно является интерполяционным. На практике наиболее часто встречается интерполяция многочленами первой, второй и третьей степени (линейная, квадратичная и кубическая интерполяции). соответствующие формулы для записи многочленов Лагранжа первой и второй степени:

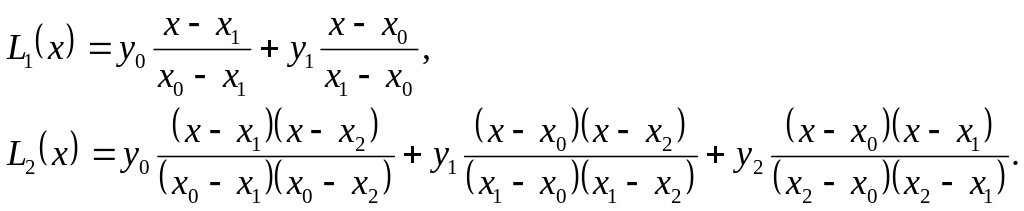
Интерполяция многочленом степени п имеет (п+1)-й порядок точности относительно h_max.

14

Минимизация погрешности оценки интерполяции. Многочлены Чебышева. Постановка задачи минимизации оценки погрешности.

Предположим, что значение заданной на отрезке [a, b] функции f можно вычислить в произвольной точке х. Однако по некоторым причинам, например, вследствие трудоемкости вычисления значений f(x), целесообразнее заменить прямое вычисление функции f вычислением значений ее интерполяционного многочлена Р(х). Для такой замены необходимо получить таблицу значений функции f в выбранных на отрезке [a, b] точках х₀, х₁, … , х_п. При этом естественно стремиться к такому выбору узлов интерполяции, который позволит сделать минимальной величину

- погрешность интерполяции на отрезке [a, b].

Пусть о функции f известно лишь то, что она непрерывно дифференцируема (п+1) раз на отрезке [a, b]. Поставим теперь задачу: определить набор узлов интерполяции х₀, х₁, … , х_п , при котором величина минимальна. Для решения этой задачи нам потребуются некоторые сведения о многочленах Чебышева.

Многочлены Чебышева.

Введенные П.Л.Чебышевым многочлены Т_п(х) широко используются в вычислительной математике. При п=0 и п=1 они определяются явными формулами

Т₀(х) = 1, Т₁(х) = х,

а при п  2 рекуррентной формулой

Т_п(х) = 2хТ_п-1(х) - Т_п-2(х) .

Запишем явные формулы многочленов Чебышева для п = 2, 3, 4, 5:

Т₂(х) = 2хТ₁(х) - Т₀(х) = 2х² - 1,

Т₃(х) = 2хТ₂(х) - Т₁(х) = 4х³ - 3х,

Приведем некоторые свойства многочленов Чебышева.

1. При четном п многочлен Т_п(х) содержит только четные степени х и является четной функцией, а при нечетном п многочлен Т_п(х) содержит только нечетные степени х и является нечетной функцией.

2. При п  1 старший коэффициент многочлена Т_п(х) равен 2^п-1 .

Справедливость свойств 1 и 2 следует непосредственно из определения многочленов Чебышева.

3. Для х-1; 1 справедлива формула T_n(x) = cos(n arccosx). (30)

Доказательство. При п = 0 и п = 1 формула (30) справедлива. Для того, чтобы доказать ее справедливость для всех п  2, достаточно показать, что функции С_n(x) = cos(n arccosx) удовлетворяют такому же, как и многочлены Чебышева, рекуррентному соотношению С_n(x) = 2xC_n-1(x) - C_n-2(x) . (31)

Соотношение (31) получится, если в легко проверяемом тригонометрическом тождестве cos[(m+1)] + cos[(m-1)] = 2cos cosm

положить т = п-1 и  = arccosx .

4. При п  1 многочлен Т_п(х) имеет ровно п действительных корней, расположенных на отрезке [-1; 1] и вычисляемые по формуле

к = 0, 1, … , п-1.

5. При п  0 справедливо равенство 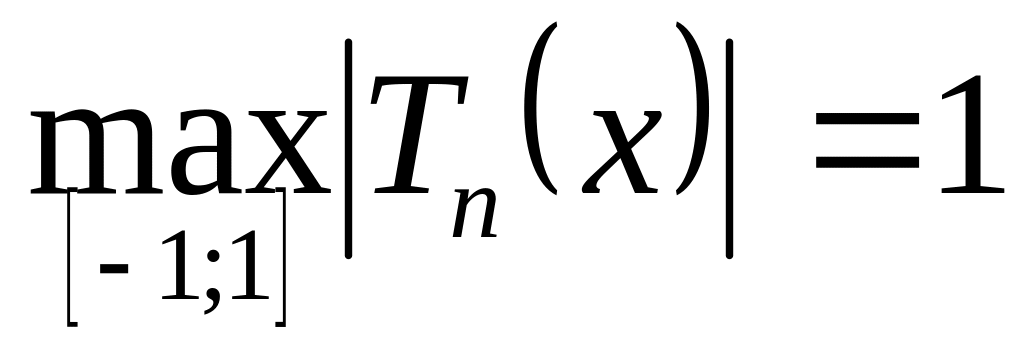. Если п  1, то этот максимум достигается ровно в п + 1 точках, которые находятся по формуле

, т = 0, 1, … , п .

При этом максимумы и минимумы многочлена Чебышева чередуются.

Свойства 4 и 5 следуют из формулы (30).

Назовем величину уклонением многочлена Р_п(х) от нуля.

6. Среди всех многочленов фиксированной степени п  1 со старшим коэффициентом а_п, равным 1, наименьшее уклонение от нуля (равное 2^1-п ) имеет многочлен .

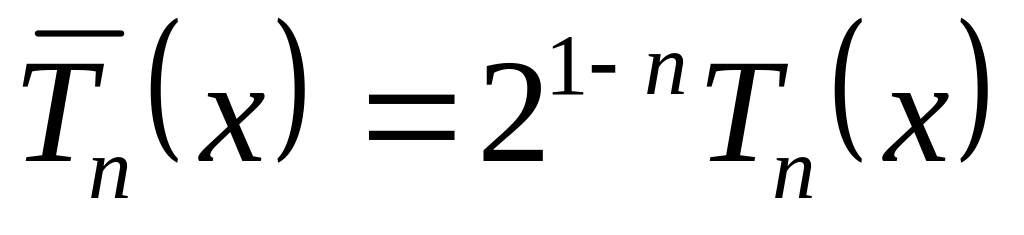Благодаря свойству 6 многочлены Чебышева иногда называют наименее уклоняющимися от нуля. Это свойство иначе можно сформулировать так: для любого многочлена вида Р_п(х) = х^п + а_п-1х^п-1 + … + а₀, отличного от , справедливо неравенство

.

Решение задачи минимизации оценки погрешности.

Найдем сначала решение задачи в предположении, что отрезок интерполяции [a, b] совпадает с отрезком [-1; 1].

Если функция f непрерывно дифференцируема (п+1) раз на отрезке [a, b], то имеем формулу

где _п+1(х) = (х - х₀)(х - х₁)…(х - х_п), а  - некоторая точка, принадлежащая интервалу (a, b); для верхней границы погрешности интерполяции эта формула дает

. (31)

Здесь .

Величина (31) будет минимальной при таком выборе узлов х₀, х₁, …, х_п, при котором минимальна величина , т.е. минимально уклонение многочлена _п+1(х) от нуля. В силу свойств 4 и 6 многочленов Чебышева решение задачи дает набор узлов , к = 0, 1, …, п,

являющихся нулями многочлена Т_п+1, т.к. в этом случае . при таком выборе, причем в силу свойства 6 многочленов Чебышева любой другой выбор узлов дает большее значение верхней границы погрешности.

Пусть теперь отрезок интерполяции [a, b] произволен. Приведем его к стандартному отрезку [-1, 1] заменой ,

где t[-1, 1]. В этом случае аналогичное рассмотрение дает следующий выбор узлов:

, к = 0, 1, … , п.

15-16-17