3.4.Порядок выполнения работы

1. Составить систему уравнений для метода интерполяции и решить ее относительно коэффициентов a_m, меняя количество базисных функций первого вида от 1 до 5.

2. Используя полученные коэффициенты, построить графики аппроксимирующих функций.

3. Повторить пп. 1 и 2 для второй системы базисных функций.

4. Составить уравнения для определения элементов матрицы K и вектора f для метода взвешенных невязок.

5. Используя полученные значения, определить коэффициенты a_m и построить графики аппроксимирующих функций.

6. Проанализировать полученные результаты.

7. Составить программу для расчета поля в прямоугольном желобе при помощи процедур-функций relax и multigrid.

8. Решить задачи, используя сеточные области с различным числом узлов.

9. Сравнить полученные решения с аналитическим в различных точках квадратной области и построить зависимость погрешности решения от числа узлов сеточной области.

3.5.Содержание отчета

1. Программа, реализующая алгоритм аппроксимации при помощи двух заданных видов базисных функций.

2. Графики аппроксимируемых и базисных функции.

3. Графики аппроксимирующих функций для различного количества базисных функций.

4. Программа для решения уравнения Лапласа, использующая стандартные процедуры-функции relax и multigrid.

5. Графики распределения потенциала в серединном сечении, полученные численными методами и аналитически.

4.Моделирование систем формирования магнитного поля численным методом

Цель работы – освоение практической работы с программой расчета магнитостатических задач “Тесла”, основу которой составляет конечно-разностный метод решения уравнения Пуассона; исследование точности полученных приближенных решений путем их сравнения с известным аналитическим решением тестовой задачи; исследование скорости сходимости решения задачи, получаемого по методу последовательных приближений, используемого в программе “Тесла”, в зависимости от заданных параметров, вводимых в программу расчета.

4.1.Основные особенности математической модели, используемой в программе расчета магнитных систем “Тесла”

Математическая модель расчета магнитных систем основывается на исходных дифференциальных уравнениях магнитостатики, которые сводятся, в конечном счете, к уравнению Пуассона. В аксиально-симметричном случае в цилиндрической системе координат это уравнение записывается следующим образом:

, (4.0) где  – нормированный магнитный поток;  – плотность тока соленоидов; j – плотность связанных токов.

Связанные токи возникают на поверхности и в объеме детали из ферромагнитных материалов. Токи  и j имеют только одну азимутальную составляющую.

Результатом решения уравнения (4.1) является распределение магнитного потока (z, r), по которому можно найти составляющие вектора магнитной индукции по формулам

.

Уравнение (4.1) решается конечно-разностным методом на прямоугольной сетке, каждому узлу которой соответствует конечно-разностный аналог уравнения Пуассона.

При использовании 5-точечного сеточного шаблона магнитный поток в центральном узле шаблона ₀ определяется по значениям магнитных потоков _i в четырех узлах, окружающих этот узел,

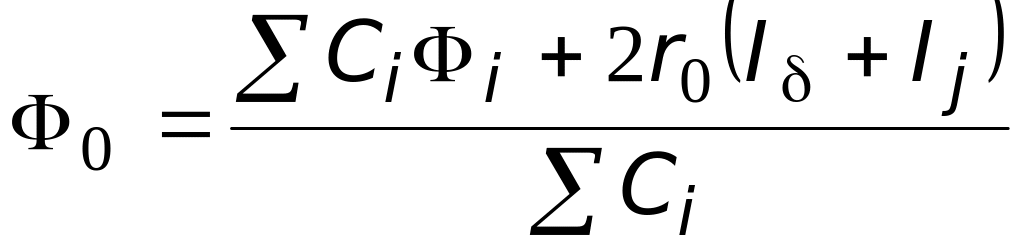. (4.0) Здесь коэффициенты C_i являются функциями плеч (расстояний между соседними узлами) h_i сеточного шаблона и расстояния r₀ от центрального узла шаблона до оси симметрии; I_ и I_j – токи соленоида и связанные токи, привязанные к центральному узлу.

При использовании уравнения (4.2) для каждого внутреннего узла сеточной области образуется система линейных алгебраических уравнений, порядок которой при большом количестве узлов сетки может достигать нескольких десятков тысяч. В этих условиях систему алгебраических уравнений целесообразно решать методом последовательных приближений, состоящих из определенного количества одинаковых итераций.

В каждой отдельной итерации получают некоторое промежуточное решение для магнитного потока во всех внутренних узлах сетки, которые заменяют значения , полученные на предыдущей итерации. Такой процесс является сходящимся при любых начальных условиях, в том числе и при нулевых значениях магнитного потока внутри сеточной области. Процесс сходимости контролируется по значению невязки , рассчитываемой для каждого узла сеточной области. Если для всех узлов сетки значение невязки становится меньше заданного в программе предельного значения погрешности _Ф, решение задачи считается законченным.

Количество необходимых для получения решения итераций прежде всего зависит от таких факторов, как количество узлов сеточной области и заданных условий на границе сеточной области. В любом случае процесс сходимости может быть ускорен, если воспользоваться теорией Янга–Франкела о последовательной верхней релаксации. В соответствии с этой теорией значения потоков на каждой итерации определяются по следующей формуле:

, где – значения потока в узле на предыдущей итерации; – значение потока на данной итерации, полученное по формуле (4.2);  – коэффициент верхней релаксации, значения которого выбираются в интервале от 1 до 2. Из теории Янга–Франкела следует, что для каждого конкретного случая существует оптимальное значение _opt, при котором количество итераций, необходимое для сходимости задачи, минимально. На рис. 4.1 представлена типичная зависимость необходимого числа итераций N как функция от заданного при расчете значения параметра верхней релаксации . Эта зависимость N() получена для решения уравнения Лапласа на квадратной сетке с равномерным шагом. Приведены два варианта расчета для сетки 1616 и 3232. Оптимальные значения для этих вариантов соответственно, равны 1.67 и 1.82. При этом абсолютная погрешность расчета _Ф составляла 10^–14.

Рис. 4.1. Зависимость количества итераций от коэффициента релаксации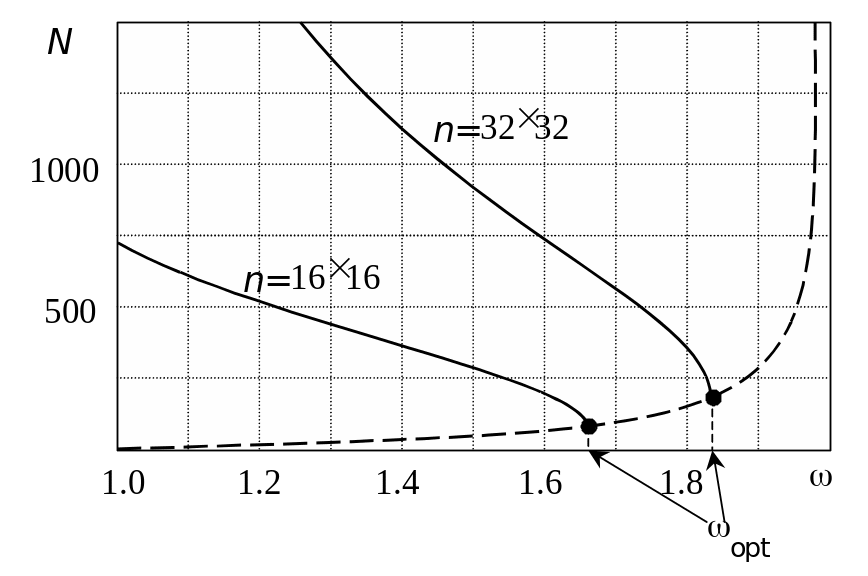

Программа “Тесла” позволяет использовать двухмерную прямоугольную сетку с кусочно-постоянным шагом по каждой координате, что дает возможность регулировать шаг сетки в различных ее частях в зависимости от конструктивных особенностей элементов магнитной системы. Нижняя сторона прямоугольной сеточной области совпадает с осью z, где магнитный поток равен нулю. На трех других границах области возможно задание одного из трех условий: .

Граничное условие соответствует наиболее распространенному случаю, когда границу сеточной области замыкают вокруг всех элементов магнитной системы в непосредственной близости от них. В каждой точке границы рассчитывается аналитически путем суммирования воздействия на магнитный поток со стороны всех источников магнитного поля, входящих в правую часть уравнения Пуассона.

В данной работе в качестве источников используются только токи соленоидов.

Граничное условие позволяет уменьшить объем вычислений для систем, обладающих плоскостью симметрии, перпендикулярной оси z, производя расчеты для половинки таких магнитных систем.

При численном расчете полевых задач встает вопрос о точности получаемых решений. При этом анализируются в основном два типа погрешностей [2], [6]. Первый тип связан с ошибками округления, вызванными ограниченной разрядностью представления чисел в памяти компьютера. В каждом узле сетки магнитный поток рассчитывается с некоторой ошибкой, которая в дальнейшем распространяется на остальные узлы. Уменьшить ошибку можно за счет увеличения разрядности представления действительных чисел (обычно используется двойная и даже четверная точность).

Второй тип погрешности заключен в самом методе сеток и определяется степенью дискретизации при замене непрерывного оператора Лапласа его конечно-разностным аналогом. Этот тип погрешности связан с размером шага сетки и типом шаблона, применяемым при определении конечно-разностной формулы. В этом случае погрешность может быть уменьшена при уменьшении шага сетки и использовании конечно-разностной формулы более высокого порядка (например 9-точечный шаблон). Оценка этого типа погрешности произведена только для самых простых случаев, например для единичного квадрата. Для 5-точечного шаблона конечно-разностная формула дает погрешность порядка h².

В данной работе оценка погрешностей производится сравнением результатов численного расчета с решением тестовой задачи о магнитном поле соленоидов.