2.2.Расчет траекторий заряженных частиц с использованием уравнений движения в форме Лагранжа
Очень хорошим тестом для проверки точности работы численных алгоритмов расчета траекторий движения заряженных частиц в электрических и магнитных полях является задача о движении заряда в поле точечного магнитного заряда , который можно представить, как один из полюсов очень тонкого прямолинейного магнита такой большой протяженности, что действием второго полюса можно пренебречь.
Учитывая симметрию поля, целесообразно выбрать сферическую систему координат, в которой вектор напряженности магнитного поля H будет иметь только одну радиальную составляющую Hr /r2.
В этом случае векторный потенциал A также имеет только одну отличную от нуля составляющую
.
Для описания движения заряженной частицы воспользуемся уравнением Лагранжа для материальной точки
.
Поскольку функция Лагранжа L для заряженной частицы, движущейся в электрическом и магнитном полях, имеет вид
,
в
сферической системе координат в
нерелятивистском приближении для нашей
задачи получаем
.
Но тогда из уравнений Лагранжа следует:
;
; (2.0)
. (2.0)
Если проинтегрировать уравнение (2.7), то получим
, (2.0)
где
R1
– константа, зависящая от начальных
условий.
Если же в уравнении (2.7) вычислить производную по времени в левой части и затем разделить обе части уравнения на sin , получим
. (2.0)
Умножив (2.9)
на
и (2.6) на
,
а затем сложив полученные выражения,
после небольших преобразований можно
представить результат в виде
,
откуда
. (2.0)
При умножении
(2.9) на
и (2.6) на
и аналогичных вычислений, получим
. (2.0)
Из равенств (2.7), (2.9) и (2.10) следует, что константы R1, R2 и R3 представляют собой проекции постоянного вектора
.
Решение задачи можно упростить, если совместить ось с направлением постоянного вектора R. При этом движение будет происходить по конической поверхности const. В этом случае
.
Подставляя указанные выражения в (2.7), получим
. (2.0)
Используем закон сохранения энергии для построения траектории на конической поверхности. В сферической системе координат в поле магнитного заряда этот закон выглядит следующим образом:
.
Исключая при помощи (2.12) дифференцирование по времени и учитывая постоянство координаты на поверхности конуса, получим дифференциальное уравнение
,
определяющее
зависимость r
от .
В результате разделения переменных
получается уравнение
,
из
которого в результате интегрирования
получается искомая зависимость
,
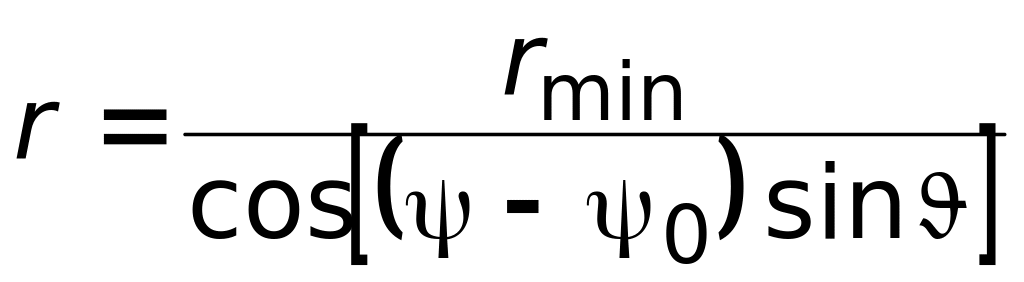где
– наименьшее расстояние, на которое
частица может приблизиться к магнитному
заряду.
2.3.Расчет траекторий заряженных частиц численными методами
При анализе реальных систем электрические и магнитные поля из-за своей сложности, как правило, рассчитываются с помощью численных методов на дискретном множестве. В этом случае аналитическое решение уравнения движения невозможно, и для построения траекторий движения заряженных частиц в таких полях используются также различные численные методы решения дифференциальных уравнений.
В основе численных методов решения дифференциальных уравнений лежит алгоритм, согласно которому процесс решения дифференциального уравнения первого порядка сводится к выбору некоторой начальной точки, вычислению тангенса угла наклона кривой y = y(x) и перемещению на небольшое расстояние в полученном направлении для определения следующей точки [7], [8]. Далее процесс необходимо повторять, всякий раз используя новую точку кривой как начальную.
Используемые на практике методы численного интегрирования отличаются от описанного метода тем, что позволяют избежать ошибок в тех случаях, когда значение производной сильно меняется в пределах того малого расстояния (шага интегрирования), на котором численный метод осуществляет перемещение по неизменному направлению (см. рисунок), поскольку для получения каждой следующей точки используется тангенс угла наклона касательной в предыдущей. В этих методах сначала производится пробный шаг, имеющий целью определить тенденцию к изменению тангенса угла наклона, а затем выполняется собственно шаг интегрирования в направлении среднего арифметического начального и конечного тангенсов угла наклона. Таким образом, сначала определяется положение пробной точки
,
а
затем, используя корректирующую формулу
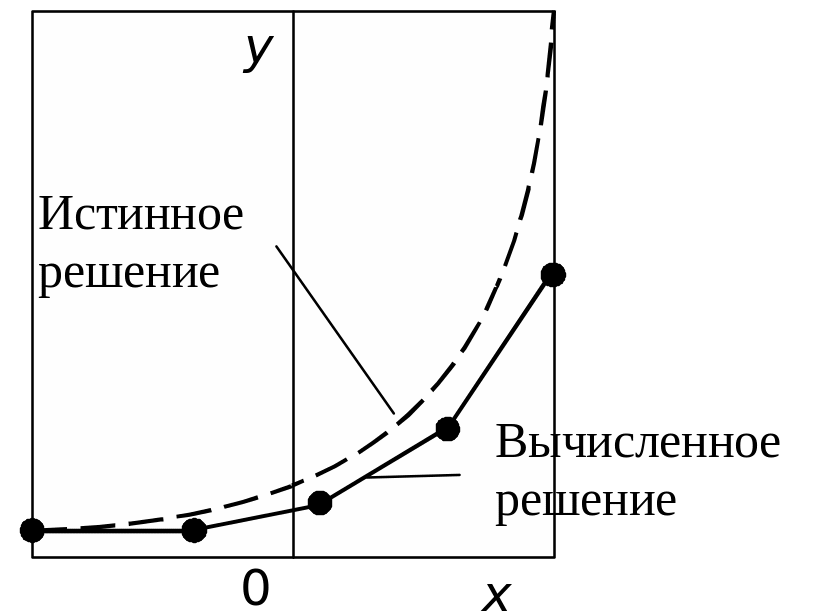Численное
решение дифференциального уравнения
,
выполняется
шаг интегрирования. Такая схема проведения
численного решения дифференциальных
уравнений (или численного интегрирования)
называется схемой прогноза и коррекции.
Основная проблема, с которой приходится сталкиваться в схемах прогноза и коррекции, состоит в определении достаточного числа начальных значений, для того чтобы начать прогноз. Чаще всего для этих целей используется один из вариантов метода Рунге–Кутта. Наиболее распространенным вариантом можно считать тот, когда для заданных
последовательно
вычисляются:
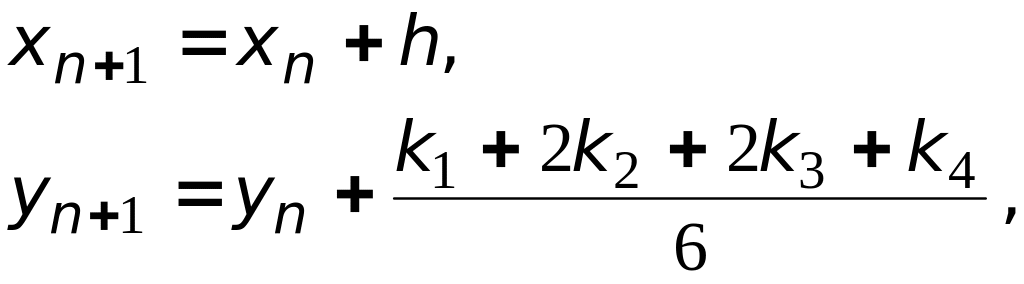где
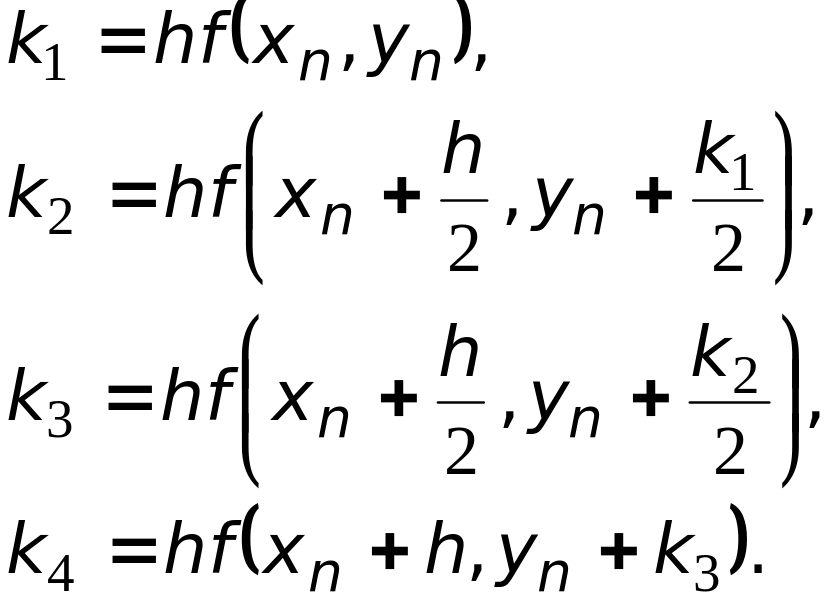
Этот процесс становится особенно понятным, если дать его геометрическую интерпретацию. В точке (xn, yn) вычисляется тангенс угла наклона, который просто равен значению f(xn, yn) в данной точке. Далее, используя полученное значение тангенса угла наклона и заданное значение шага интегрирования h вдоль координаты x, определяется значение k1 первого пробного шага вдоль y. Выполнив первый пробный шаг на половину его рассчитанной длины, определяется новое значение тангенса угла наклона и, соответственно, значение k2 второго пробного шага вдоль y. Для вычисления k3, определяющего длину третьего пробного шага вдоль y, используется такая же процедура, а для четвертого пробного шага вдоль y, т. е. для k4, третий шаг выполняется на всю свою длину. После того как длины всех четырех пробных шагов вдоль y окажутся вычисленными, производится окончательный шаг интегрирования из (xn, yn) в (xn+1, yn+1), где тангенс угла наклона определяется методом усреднения по четырем пробным тангенсам с весами 1, 2, 2 и 1.
В системе MathCAD используется метод Рунге–Кутта четвертого порядка, реализованный в виде функции rkfixed, которая возвращает матрицу, состоящую из (n+1) столбцов:
первый столбец содержит точки, в которых ищется решение дифференциального уравнения;
второй и последующие столбцы содержат значения найденной функции и ее производных с первой по (n–1)-ю в соответствующих точках.
Для получения результата необходимо написать строку вида
z rkfixed (y, x1, x2, npoints, D), где y – вектор начальных условий размерности n, где n – порядок дифференциального уравнения; x1, x2 – граничные точки интервала, на котором ищется решение дифференциального уравнения (начальные условия, заданные в y, – это значение решения в точке x1); npoints – число точек (не считая начальной), в которых ищется приближенное решение; D(x, y) – функция, возвращающая значение в виде вектора, состоящего из n элементов, содержащих производные неизвестной функции от первого до n-го порядка; z – матрица размером (n+1) (npoints + 1).