3.2.Расчет электростатических полей в декартовой системе методом конечных разностей

Уравнение Пуассона

(3.0) и его однородную форму – уравнение Лапласа, являющиеся дифференциальными уравнениями в частных производных с заданными граничными условиями вида, во многих практических случаях выгоднее решать численными методами. При этом решение получается не в виде аналитических функций, которые могут использоваться для расчета в произвольной точке области, а в виде значений искомой функции в отдельных, выбранных заранее точках области.

Процедура задания набора фиксированных точек, а также правил расчета функции в этих точках называется дискретизацией.

Наиболее простым с точки зрения программирования и математического обоснования является метод конечных разностей. В основу этого метода положено разложение функции в ряд Тейлора, при помощи которого производится замена непрерывной частной производной второго порядка ее конечно-разностным аналогом с погрешностью порядка O(h³).

В окрестности точки (x, y) функцию U(x, y) можно разложить в ряд Тейлора по координате x двумя способами:

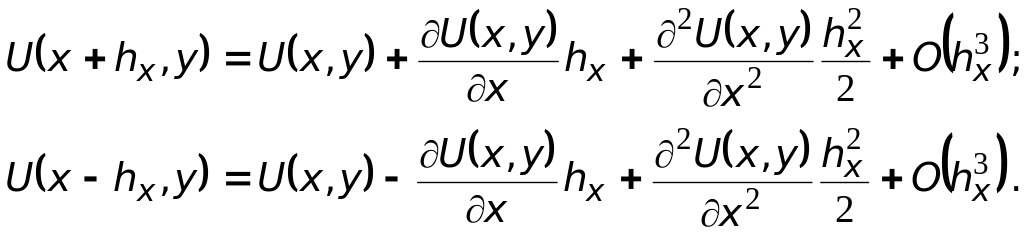
Складывая эти два ряда и отбрасывая члены третьего порядка малости по h, получим

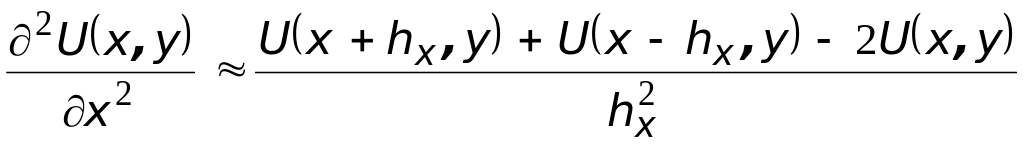. (3.0)

Аналогично можно разложить функцию U(x, y) по координате y:

откуда с точностью до O(h³) получим

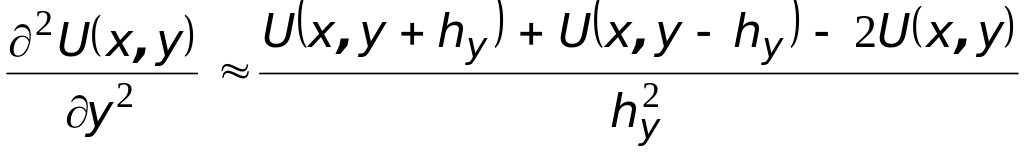. (3.0)

Выбирая сетку таким образом, чтобы соседние узлы отстояли друг от друга по координатам x и y на расстоянии h_x и h_y и подставляя (3.2) и (3.3) в (3.1), после небольших преобразований получим конечно-разностный аналог уравнения Пуассона:

, (3.0) с помощью которого значение функции в узле с номером (j, k) может быть рассчитано по значениям функции в 4 соседних узлах c номерами (j+1, k), (j–1, k), (j, k+1) и (j, k–1).

В MathCAD имеются две функции для решения дифференциальных уравнений в частных производных в области с квадратной границей.

Если функция U(x, y) имеет нулевые граничные условия на всех сторонах квадрата, то для нахождения этой функци лучше использовать

U  multigrid (M, 2), где M – квадратная матрица размером 1+2ⁿ, содержащая значения правой части уравнения (3.4) в соответствующих точках квадрата.

Процедура-функция relax позволяет найти решение уравнения Пуассона при ненулевых граничных условиях на сторонах квадрата

U  relax (a, b, c, d, e, f, g, rJac), где a, b, c, d, e – квадратные матрицы одинакового размера, содержащие соответствующие коэффициенты уравнения (3.4); f – квадратная матрица, содержащая значения правой части уравнения (3.4) в соответствующих точках квадрата; g – квадратная матрица, содержащая значения решения на границе области (граничные условия) и начальное приближение для решения внутри области в соответствующих точках квадрата; rJac – спектральный радиус итераций Якоби в интервале от 0 до 1, управляющий сходимостью алгоритма релаксации.

3.3.Задание по работе

Аппроксимировать функции z₁ = Ae^x+Be^–x и z₂, заданную в виде таблицы, методом интерполяции и методом взвешенных невязок, используя в качестве базисных функций

N_m = x^m(1–x); m = 1, 2, 3 …

N_m = sin (mx/L_x); m = 1, 2, 3 …

на отрезках [0, 1], [1, 2], [0, 2], [–1, 1] …

Узловые точки выбираются по вариантам.

Таблично задаваемая функция (см. рисунок) определяется в виде экспериментальных значений отклонений z(x, y) квадратной пластины со сторонами единичной длины, находящейся под действием нагрузки, и закреплены-

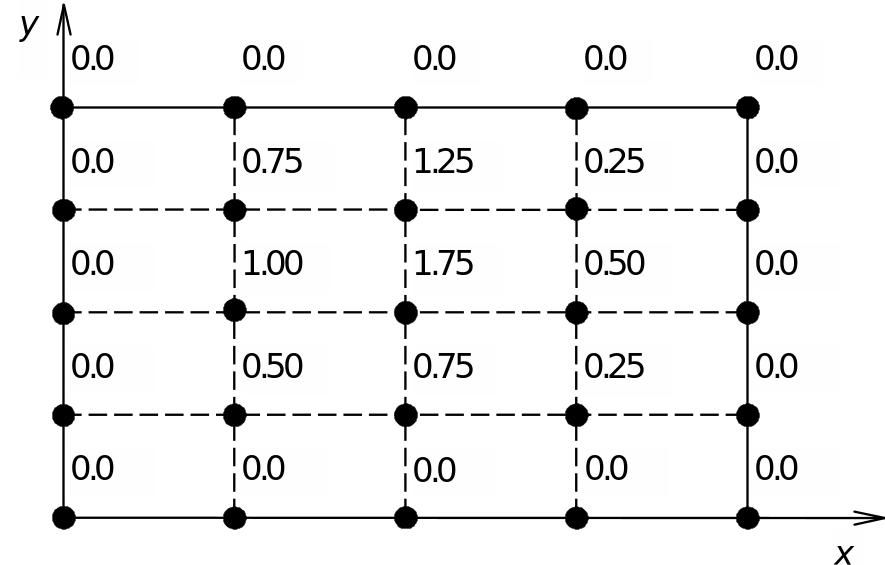
ми краями.