1.2.Расчет электростатических полей в цилиндрической системе координат методом разделения переменных

Для электростатических полей, имеющих осевую симметрию, решение уравнения Лапласа может быть представлено в виде

, (1.0) где параметры k, A_k, B_k, C_k и D_k определяются из граничных условий задачи.

В

Рис. 1.4. Сечение цилиндрического стакана с криволинейной крышкой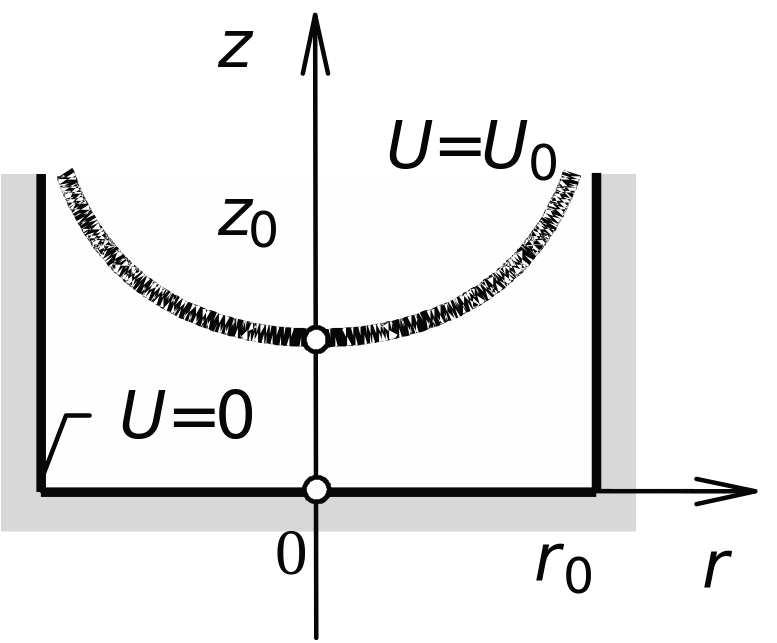

качестве примера решения задачи электростатики в цилиндрической системе координат можно рассчитать форму крышки для цилиндрического стакана (рис. 1.4), которая позволяет определять потенциал при помощи всего одного частного решения уравнения Лапласа, соответствующего какому-то выбранному значению k. При этом стенки и дно цилиндрического стакана находятся под нулевым потенциалом, а крышка изолирована от самого стакана и имеет потенциал U₀. Радиус стакана и радиус крышки равны одному и тому же значению r₀. Ось симметрии стакана направлена вдоль оси z. Ближайшая к дну стакана точка крышки расположена на оси симметрии на расстоянии z₀ от дна.

Согласно условию задачи граничные условия выглядят следующим образом: 1) U  0 при z  0; 2) U  0 при r  r₀; 3) U ограничена на оси (при r  0); 4) U  U₀ при z  z₀, r  0.

Поскольку и функция Неймана при r  0 и гиперболический косинус при z  0 неограниченны, то для выполнения первого и третьего условий коэффициенты A_k и D_k в (1.8) должны равняться нулю. В результате, частное решение, которое требуется исследовать в данной задаче, приводится к виду

. (1.0)

Для выполнения второго граничного условия необходимо, чтобы произведение k_mr₀ совпадало с каким-либо корнем функции Бесселя нулевого порядка, т. е. k_mr₀  _0m, где _0m – m-й корень функции J₀(x).

Используя четвертое граничное условие и тот факт, что при r  0 функции Бесселя нулевого порядка J₀(x)   1, можно определить значение постоянной U_m:

.

Форма любой эквипотенциальной поверхности может быть рассчитана, если исходное уравнение преобразовать к виду

.

Для определения формы второго электрода в качестве const необходимо взять U₀ и тогда

.

Рис. 1.5. Сечение цилиндрического стакана с прямолинейной крышкой

Подставляя в приведенное уравнение различные значения r, будем получать соответствующие значения z.

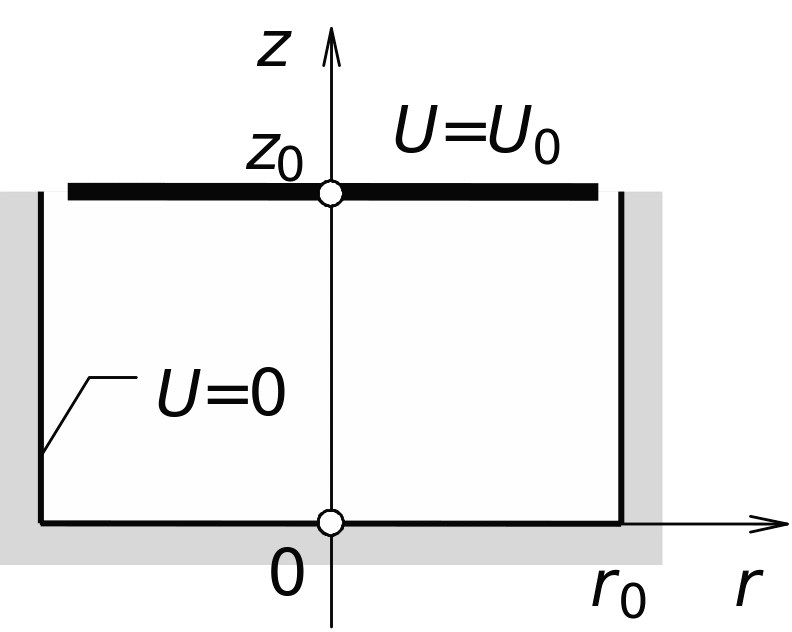
В последней задаче данной работы надо найти распределение потенциала в круглом заземленном цилиндре, закрытом плоской крышкой, которая изолирована от самого цилиндра и имеет потенциал U₀ (рис. 1.5). Высота цилиндра равна z₀, а радиус – r₀.

По сравнению с предыдущей задачей четвертое граничное условие заменяется на U(z₀, r)  U₀.

Подобные условия на границе не могут быть выполнены с помощью одной какой-либо функции вида (1.9). Однако и в этом случае удается представить решения как сумму частных решений вида

, (1.0) где k_m = _0m/r₀.

Данный метод решения основан на ортогональности функций Бесселя и позволяет представить любую кусочно-гладкую функцию на интервале от 0 до a в виде ряда Фурье–Бесселя

, (1.0) где коэффициенты A_m для случая, рассматриваемого в задаче, определяются по известной из теории этих рядов формуле

.

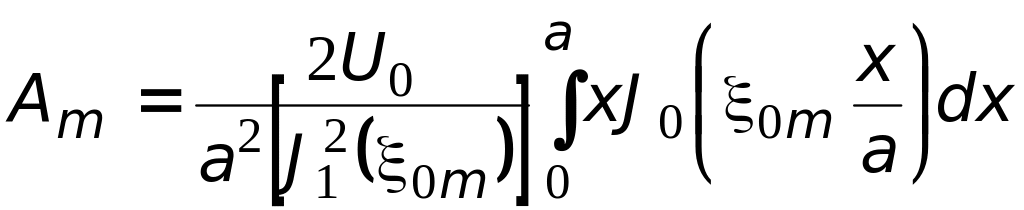Используя правила дифференцирования и интегрирования функций Бесселя, получим

.

Поскольку ряды (1.10) и (1.11) должны описывать по нашему замыслу одну и ту же функцию, коэффициенты у подобных членов обоих рядов должны быть равными между собой. Отсюда получаем выражение для определения U_m:

, откуда уже следует окончательная формула

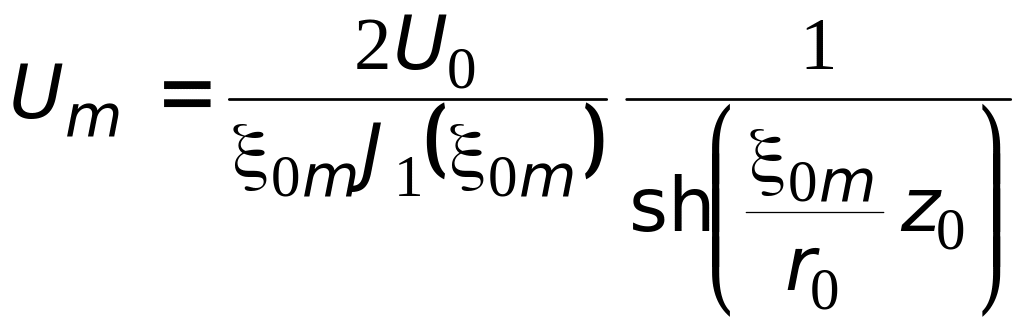, которая после подстановки в (1.10) позволяет записать решение в виде

.
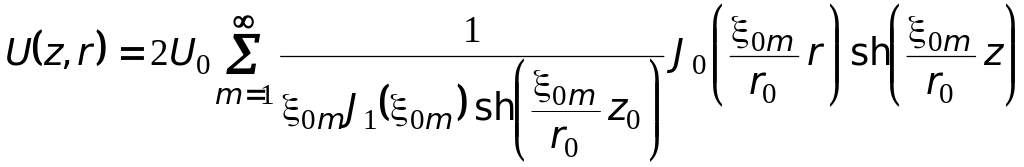