1.3.Порядок выполнения работы

1. Написать программу для расчета формы крышки к бесконечному прямоугольному желобу, создающей внутри желоба электростатическое поле, для описания которого достаточно всего лишь одного частного решения уравнения Лапласа в декартовой системе координат.

2. Изобразить на графике форму крышки и формы эквипотенциальных линий 0.8 U₀, 0.6 U₀, 0.4 U₀, 0.2 U₀, 0.1 U₀.

3. Построить трехмерный график зависимости потенциала U от координат x и y.

4. Написать программу для расчета потенциала внутри бесконечного прямоугольного желоба, накрытого плоской крышкой.

5. Изобразить на графике эквипотенциальные линии 0.8 U₀, 0.6 U₀, 0.4 U₀, 0.2 U₀, 0.1 U₀.

6. Построить трехмерный график зависимости потенциала U от координат x и y.

7. Рассчитать таблицу значений потенциала в сечении xy и построить зависимость точности решения от количества членов ряда.

8. Рассчитать первые 25 корней функции Бесселя нулевого порядка.

9. Написать программу для расчета формы крышки к цилиндрическому стакану, создающей внутри электростатическое поле, для описания которго достаточно всего лишь одного частного решения уравнения Лапласа в цилиндрической системе координат.

10. Изобразить на графике форму крышки и формы эквипотенциальных линий 0.8 U₀, 0.6 U₀, 0.4 U₀, 0.2 U₀, 0.1 U₀.

11. Построить трехмерный график зависимости потенциала U от координат z и r.

12. Написать программу для расчета потенциала внутри цилиндрического стакана, накрытого плоской крышкой.

13. Изобразить на графике эквипотенциальные линии 0.8 U₀, 0.6 U₀, 0.4 U₀, 0.2 U₀, 0.1 U₀.

14. Построить трехмерный график зависимости потенциала U от координат z и r.

15. Рассчитать таблицу значений потенциала в сечении rz и построить зависимость точности решения от количества членов ряда.

1.4.Содержание отчета

1. Программы для расчета формы крышек, создающих простые, с точки зрения их аналитического представления, поля в декартовой и цилиндрической системах координат.

2. Графики эквипотенциальных линий.

3. Трехмерные графики зависимостей потенциала от координат xy или rz.

4. Зависимости точности решения от количества членов ряда.

2.Моделирование процессов движения заряженных частиц в электрических и магнитных полях в вакууме аналитическими и численными методами

Цель работы – исследование влияния электрического и магнитного полей на характер движения заряженной частицы, определение точности численного метода расчета траекторий и зависимости этой точности от параметров модели численного алгоритма.

2.1.Расчет траекторий заряженных частиц с использованием уравнений движения в форме Ньютона

Для построения траектории заряженной частицы с зарядом e и массой m₀, движущейся в однородных постоянных электрическом E и магнитном B полях, всегда можно выбрать декартову систему координат так, чтобы ось z совпадала с направлением магнитного поля B, а плоскость 0xz была параллельна силовым линиям электрического поля E [5]. Поскольку траектория движения инвариантна по отношению к выбору системы отсчета, то для удобства вычислений совместим начало координат с начальной точкой движения частицы так, что x₀ = y₀ = z₀ = 0. При данном выборе системы координат B_x = B_y = 0, B_z = B и E_y = 0, поэтому уравнение движения заряженной частицы в форме Ньютона

в проекциях на оси координат в нерелятивистском приближении преобразуется в систему уравнений

(2.0)

Интегрирование второго уравнения системы дает зависимость y-й составляющей скорости от x:

. (2.0)

Если подставить выражение (2.2) в первое уравнение системы (2.1), то получим неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:

.

Решением этого уравнения будет

(2.0) где .

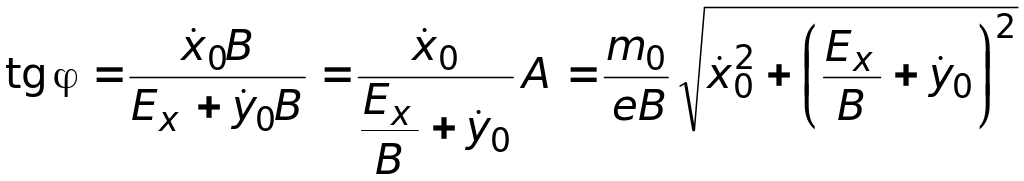Подставляя (2.3) в (2.2) и интегрируя, получим закон изменения y‑координаты частицы от времени:

(2.0)

Далее, дважды интегрируя третье уравнение системы (2.1), найдем зависимость z  z(t):

. (2.0)

Анализ полученных зависимостей приводит к следующим результатам:

, что является уравнением плоской окружности с радиусом, равным A, и координатами центра в плоскости 0xy

который движется с постоянной скоростью –E_x/B вдоль оси 0y. Это означает, что проекция траектории на плоскость 0xy представляет собой трохоиду, описываемую в параметрическом виде уравнениями (2.3) и (2.4).

Для определения пространственной формы траектории следует учитывать уравнение (2.5), согласно которому вдоль координаты z частица движется равноускоренно. Поэтому в общем случае ее траекторию можно представить в виде спиральной линии с радиусом, равным A, и осью, совпадающей с параболой в плоскости 0yz.

Угловая скорость, с которой частица движется по окружности, определяется формулой .

При этом частица делает полный оборот за время , не зависящее от напряженности электрического поля и от начальных условий.