Сп с независимыми приращениями (нп)

1. общие свойства СП с НП

2. Пуассоновский поток событий

3. Пуассоновский СП.

4. Каноническое представление ХФ СП с НП

1

называется процессом с независимыми приращениями, если для любых случайные величины , являются независимыми.

Запишем процесс в следующем виде .

1)Процесс с НП представляет собой суму независимых СВ. Тогда

– свертка Стильтьеса.

Каким образом можно найти ЗР этого СП.

Учитывая сложность нахождения ФР и ПВ используется ХФ, которая будет равна произведению ХФ каждой из величин.

Особенности этих ХФ

Рассмотрим

Критерием того, что – СП с НП является то, что отношение его ХФ в два разных момента времени и представляет собой ХФ тогда это отношение будет ХФ приращения.

На практике часто или .

Эти процессы изучал Поль Леви, он установил, что СП с НП можно представить в следующем виде

СП называется непрерывным, если

Или можно записать в другом виде:

Если у СП тогда используется первое соотношение.

Ограничимся СП с НП, у которого дисперсия конечна. Предположим, что , тогда

Введем некую функцию Оказывается, что Для того, чтобы СП был непрерывен

1) необходимо, чтобы функция была непрерывна

2) с вероятностью 1 в точке СП равен 0

У непрерывного СП могут быть разрывы первого рода в некоторых точках , однако эти точки не являются фиксированными на оси , то есть эти точки образуют случайную последовательность

СП является однородным, если любые его распределения приращения зависят от и не зависят от его положения на временной оси, тогда .

В дальнейшем будем изучать только СП с НП

Леви доказал, что любой СП с НП

где – непрерывная детерминированная функция (неубывающая).

– гауссовский СП с НП.

– пуассоновский СП с НП.

Для гауссовского СП ХФ имеет вид

1) – неоднородное броуновское движение

2) если , – однородное броуновское движение

3) если , – винеровский СП .

2

представляет собой точечный СП если являются случайными величинами с заданными вероятностными характеристиками.

П роцесс – число точек на – процесс счета событий. Это целочисленный процесс с реализациями – кусочно-постоянными функциями

Частные случаи

1) является независимой, одинаково распределенной СВ – процесс восстановления (задачи надежности).

2) – независимая СВ, распределенная по показательному закону – процесс Пуассона.

Обычно процесс Пуассона определяется следующим образом:

Пусть имеется случайная последовательность , удовлетворяющая условиям:

1) число событий , которые произошли на непересекающихся интервалах времени , то есть являются независимыми СВ.

2) вероятность того, что на промежутке произойдет более одного события равна 0, то есть .

3) число событий , которые произошли на интервале зависит только от длинны этого интервала и не зависит от его положения на временной оси (однородный СП с НП).

Этих трех условий достаточно, чтобы получить:

, ,

Это распределение Пуассона с параметрам .

Тогда автоматически следует, что

В этом случае последовательность называется пуассоновским потоком событий, тогда представляет собой однородный СП с НП.

, , .

– среднее число событий за единицу времени.

– непрерывная.

При условии 3) процесс является однородным.

Если убрать это предположение, то в этом случае

Условия :

1)

2) – неубывающая функция.

, где – интенсивность пуассоновского потока событий, так как – неубывающая функция.

3

Если – пуассоновский поток событий, то процесс – процесс Пуассона.

:

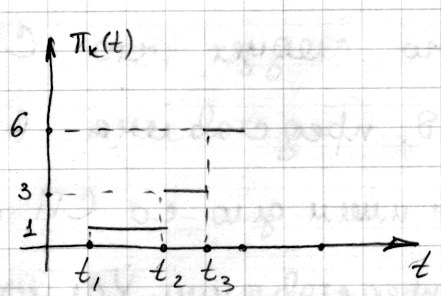
Реализации процесса Пуассона имеет вид

Для того, чтобы процесс был непрерывен необходимо

1)

2) – неубывающая

3) непрерывна

Данный процесс – процесс с непрерывными приращениями, в общем случае неоднородный и стахостически непрерывен.

Основные характеристики Пуссоновского СП

Тогда

Кумулянты из последней формулы будут иметь вид

– одномерные

,

Корреляционная функция. Рассмотрим

Если – пуассоновский СП является однородным.

– безразмерная функция, среднее число событий, которые произошли за промежуток времени .

Формула для будет одинакова как для однородных, так и для неоднородных СП.

Такого типа процесс – простой процесс Пуассона.

Рассмотрим сложный процесс Пуассона.

, где – пуассоновский СП.

– независимая, одинаково распределенная СВ с ФР или ХФ

1) Пусть : вырожденная СВ, то есть

2) :

в данном примере будут иметь разные ЗР

3) :

4) Пусть – имеет показательный ЗР

Что можно сказать о мгновенных значениях – они непрерывны.

Если – дискретная СВ – – дискретный СП

– непрерывная СВ – – СП с непрерывными мгновенными значениями.

ХФ для сложного процесса Пуассона равна:

, где

Условие однородности сложного процесса Пуассона –

4

Процесс с независимыми приращениями определяется как

1)

2) таким образом

3) ,

Где – ХФ приращений.

Из этого следует, что СП с НП и БДЗР тогда ХФ может быть представлена в трех канонических представлениях.

Так как мы имеем дело со СП с конечной энергией, запишем ХФ в каноническом представлении Калмогорова:

Рассмотрим ХФ пуассоновского сложного процесса

Получаем

Предположим

,

Если следовательно СП имеет вид

– Пуассоновская спектральная функция сложных пуассоновских процессов.

Если

1)

2)

Тогда СП с НП называют однородным СП с НП.

На основании выше сказанного

Что соответствует

Если у СП с НП и то СП состоит только из пуассоновской составляющей – конечная или счетная сумма независимых сложных пуассоновских процессов.