Нелинейные преобразования сп

1. Постановка задачи и особенности ее решения.

2. Функция распределения (ФР) отклика нелинейной системы (НС).

3. Двумерная моментная функция отклика НС.

4. Прямой метод нахождения двумерного момента отклика НС.

1

Если система инерционна (система с памятью), то решить задачу нельзя.

Ограничимся безинерционным классом систем.

,

– динамическая характеристика системы.

Безинерционность системы означает, что .

Если речь идет о СП

1) Одномерные характеристики – задача решается.

2) Двумерные характеристики – более или менее, моментные функции – какие то решения есть.

Какие характеристики воздействия надо знать, чтобы получить необходимые характеристики отклика?

2

Если есть СП с ФР , есть функциональное преобразование .

, необходимо найти ФР отклика, то есть

Общий ход решения задачи.

Фиксируем точку . Нас интересует , – преобразование функции

Задача решается в явном виде если является обратной функцией ( – монотонная функция).

3

3.1. Одномерная моментная функция

надо найти , а если не нашли.

Все центральные моментные функции вычисляются через начальные моментные функции.

3.2. Пусть имеет непрерывные мгновенные значения, то есть существует

Центральные моментные функции выражаются через начальные моментные функции.

4

Прямой метод основан на разложении двумерной плотности вероятности (ПВ) воздействия в ряды. Наиболее целесообразно использовать ортогональные ряды.

и эта система обладает следующими свойствами

Система ортонормированна

Если есть произвольная функция , , тогда может быть представлен в виде:

, где – скалярное произведение.

Условия ортогональности можно обобщить вводя так называемые весовые функции.

Для отклика нелинейной системы

Необходимо двойной интеграл привести к повторному.

Рассмотрим систему функций и эта система удовлетворяет

Ортонормированная система с весом

Если – интегрируемость квадрата на бесконечности, тогда

,

Если речь идет о двумерной плотности вероятности

Подставим в выражение для

Таким образом

Частный случай, когда получим

Если удастся разложить двумерную ПВ в ряд, то в задаче нахождения двумерного момента отклика НС сводится к вычислению . В частности для необходимо вычислить . Результат –выражение в виде ряда.

Трудности: 1) технически трудно вычислить , , , ;вычислить ; 3) выбор системы ортогональных функций и весовых функций для разложения двумерной ПВ в ряд.

Сп с дискретным спектром

1. Спектры детерминированных процессов.

2. Гармоника со случайными параметрами.

3. СП с дискретным спектром.

1

В книгах встречается следующее определение спектра СП

и соответственно

Возникает ряд вопросов: а почему находится с помощью ; почему используется преобразование Фурье и т. д.

Если есть , обладающее свойством , тогда:

1) ,

,

Инженеры используют вторую формулу представляя

2) , ,

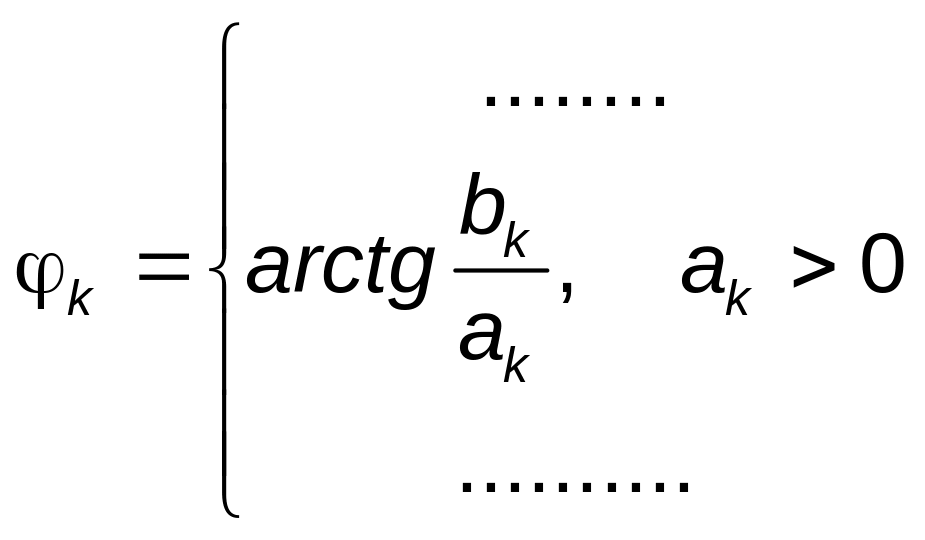
3) ,

Можем ли мы использовать все выше приведенные формулы для анализа спектра ССП ?

Напрямую ряд Фурье не применим так как ССП не обладает свойствами периодичности.

1.2) тогда , .

Вопрос: Является ли ССП сигналом с конечной энергией? – Нет , то есть не обладает конечной энергией.

2

Пуст – ССП в широком смысле.

2.1. , – СВ.

Каким условиям должны удовлетворять и чтобы был ССП.

1)

2)

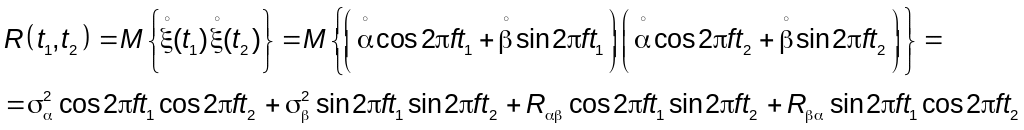
Условия: 1)

2)

3)

При этих условиях: ,

2.2. , , – независимые СВ,

Запишем исходный процесс в следующем виде

, , .

Д.з. показать, что – некоррелированны и найти дисперсию .

Таким образом накладывать условия на величины и нет необходимости – ССП

.

Пусть: 1)

2)

Таким образом для данной модели с учетом последних замечаний

2.3.

Такой процесс, в общем случае, является комплексным СП. Тогда, пусть и – комплексные СВ.

Запишем МО процесса :

Для того, чтобы был ССП необходимо:

1)

2)

Тогда корреляционная функция СП будет иметь вид

Введем следующие обозначения

1) , – комплексно сопряженные пары.

2)

Подставим в модель 2.3.

Тогда

3

3.1

Ограничения: все – независимы и имеют

: , , – некоррелированна.

Все , – независимые. Тогда характеристики СП будут равны:

Таким образом СП является стационарным в широком смысле.

Вопрос: можно ли

Вспомним, что тогда, если необходимо

СП можно представить в виде бесконечной сумы гармоник со случайными амплитудами и начальными фазами, тогда , где амплитудный множитель перед косинусом представляет собой дисперсию амплитуды.

При этом дисперсия процесса равна суме дисперсий амплитуд гармоник.

Дискретным спектром процесса является набор амплитуд гармонических составляющих на которые раскладывается ССП .

Проведем аналогию с радом Фурье.

3.2. –данная модель является общей, так как в частном случае мы можем задать и

и модели 3.2 совпадают с и модели 3.1.

3.3. Если 1) – комплексное число, тогда

2)

Введем комплексно сопряженные пары:

1) ,

2)

Тогда СП можно записать в следующем виде:

Вводим СВ : ; ;

Данный процесс является действительным.

Отметим частные случаи:

Пусть то есть функция периодическая, то есть