3. Плотность вероятностей случайного процесса.

Если ФР случайного процесса является непрерывной по всем аргументам , то на ряду с ФР можно использовать плотность вероятностей (ПВ) в виде

Если есть плотность вероятностей, то функцию распределения тоже можно найти.

Свойства плотности вероятностей

1. Положительная определенность, т.е. .

2. Свойство нормированности

3. Согласованность

4. Свойство симметрии

4. Характеристическая функция случайного процесса

Характеристической функцией СП называется функция вида , которая представляет собой преобразование Фурье-Стилтьеса от функции распределения.

Отметим тот факт, что характеристическая функция существует для всех СП. Если процесс имеет непрерывные мгновенные значения, то характеристическая функция данного процесса определяется как Фурье преобразование от плотности вероятностей, т.е.

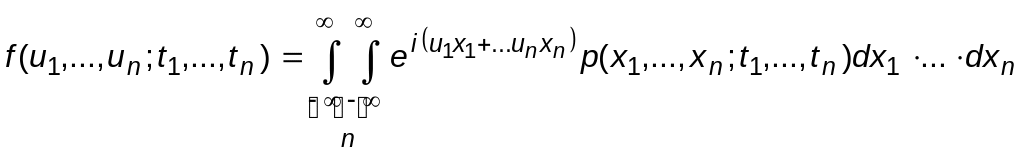
Если задана ХФ, то по ней всегда можно получить ФР или плотность вероятностей.

Свойства характеристической функции

1. Свойство нормировки, т.е. .

2. .

3. Свойство согласованности, т.е .

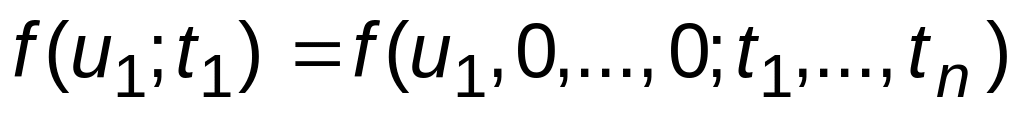4. Свойство симметрии, т.е. .

Моментные функции случайных процессов

1. Одномерные моментные функции СП.

2. Корреляционная функция СП.

3. Взаимная корреляционная функция СП.

4. Моментные функции конструктивных СП.

1. Одномерные моментные функции сп.

Математическое ожидание случайного процесса определяется в следующем виде

Определение МО: Математическое ожидание – это среднее, вокруг которого изменяются мгновенные значения СП.

Замечание!!!: Усреднение производится по всем реализациям.

В случае, когда математическое ожидание постоянно, т.е. его называют постоянной составляющей СП . МО изменяющееся во времени носит название тренда СП.

Центрированным процессом или флуктуациями называется СП вида

Для СП вводятся начальные и центральные моментные функции, которые определяются соответственно

,

,

где - порядок моментной функции.

Запишем центральный момент второго порядка, который представляет собой дисперсию СП

.

где – среднеквадратическое отклонение, определяемое как .

В свою очередь начальный момент первого порядка представляет собой математическое ожидание СП .

Дисперсия СП и его математическое ожидание выражаются друг через друга при помощи начального момента второго порядка, т.е.

Начальные и центральные моменты связаны взаимнооднозначно через характеристическую функцию

, – кумулянты.

– математическое ожидание,

– дисперсия.

Кумулянтные коэффициенты определяются следующим образом

.

2. Корреляционная функция сп

Если есть некоторые моменты времени , тогда можно ввести начальные и центральные моменты порядка

,

где ,

.

В большинстве случаев ограничиваются – что соответствует корреляционной теории СП.

Ковариационная функция и корреляционная функция СП определяются соответственно

, .

Запишем выражение связывающее ковариационную и корреляционную функции

Корреляционная функция характеризует степень линейной связи между двумя мгновенными значениями случайного процесса

,

где – интервал корреляции.

ОПРЕДЕЛЕНИЕ. Интервалом корреляции называется такой минимальный интервал времени , начиная с которого мгновенные значения случайного процесса являются некоррелированными.

Основные свойства корреляционной функции.

1. ,

2. ,

3. ,

4. ,

– нормированная корреляционная функция.

Отметим основные свойства нормированной корреляционной функции

1. ,

2. ,

3. ,

4.