
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
Рассмотрим
ось Ox,
на которой точка x
изображает акцию, а координата точки
x(t)
означает цену акции в момент времени
t.
Физические размерности: [x(t)]=руб,
[t]=мес.
Очевидно, что со временем точка х будет
перемещаться, так как цена акции
изменяется. Функцию x=x(t)
будем называть функцией
цены акции,
множество
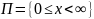 -
пространством
цен
(пространством
Блэка-Шоулса).
В простейшем случае функция x(t)
подчиняется стохастическому
дифференциальному уравнению:
-
пространством
цен
(пространством
Блэка-Шоулса).
В простейшем случае функция x(t)
подчиняется стохастическому
дифференциальному уравнению:
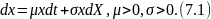
где
X
- стохастический процесс, определяемый
переходной ф-цией плотности вероятностей
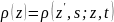 .
Дадим интерпретацию коэффициенту
.
Дадим интерпретацию коэффициенту
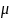 .
Пусть стоимость акции растет на p
процентов в месяц, тогда за время
.
Пусть стоимость акции растет на p
процентов в месяц, тогда за время
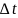 цена акции x(t)
вырастет на
цена акции x(t)
вырастет на
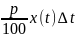 рублей и в момент времени
рублей и в момент времени
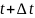 составит
составит
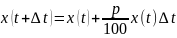 рублей. Вычислим скорость перемещения
акции в пространстве цен:
рублей. Вычислим скорость перемещения
акции в пространстве цен:
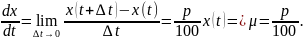
В дальнейшем будем рассматривать более общее уравнение
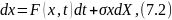
описывающее динамику цены акции.
Уравнение для плотности акций:
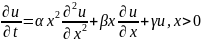
где
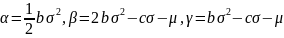
32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
формулa дифференцирования Ито стохастического процесса:
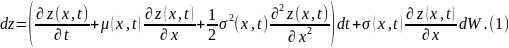
Разрешим
уравнение
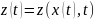 относительно x,
тогда
относительно x,
тогда
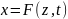 .
Подставим
в
.
Подставим
в
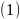 и представим ф-ции, зависящие от переменной
x,
как ф-ции переменной z.
В результате получ.стохастическое дифф.
уравн. в форме Ито для процессa
z(t):
и представим ф-ции, зависящие от переменной
x,
как ф-ции переменной z.
В результате получ.стохастическое дифф.
уравн. в форме Ито для процессa
z(t):
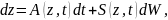 где
где
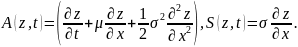
Вышеизложенное позволяет сформулировать следующее утверждение.
Утверждение.
Пусть
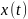 –
марковский стохастический процесс.
Рассмотр. процесс
–
марковский стохастический процесс.
Рассмотр. процесс
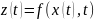 где
где
 – монотонно возрастающая ф-ция по
переменной x,
– монотонно возрастающая ф-ция по
переменной x,
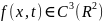 .
Тогда процесс
.
Тогда процесс
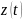 также является марковским стохастическим
процессом.
также является марковским стохастическим
процессом.
Замена переменных в уравнениях Колмогорова
Рассмотрим
условную плотность вероятностей
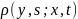 марковского
стохастического процесса X(t),
которая определяется ф-циями
марковского
стохастического процесса X(t),
которая определяется ф-циями
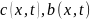 из условий сильной непрерывности. Ф-ция
подчиняется уравн. Колмогорова
из условий сильной непрерывности. Ф-ция
подчиняется уравн. Колмогорова
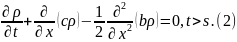
Лемма
1. Если
ф-ция
удовлетворяет уравн. (2), тогда после
замены независимых переменных
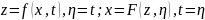 ф-ция
ф-ция
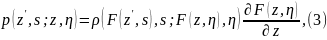
где
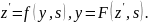
удовлетворяет уравнению Колмогорова
 где
где
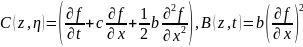
Лемма
2.
Если ф-ция
удовлетвор. уравн.
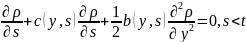 ,
тогда ф-ция (3) удовлетворяет уравн.
Колмогорова
,
тогда ф-ция (3) удовлетворяет уравн.
Колмогорова
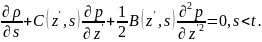
31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
Рассмотрим стохастическое дифференциальное уравнение общего вида
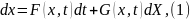
где
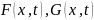 – заданные неслучайные ф-ции двух
переменных;
– заданные неслучайные ф-ции двух
переменных;
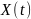 –
марковский стохастический процесс,
который определяется переходной функцией
–
марковский стохастический процесс,
который определяется переходной функцией
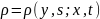 ,
которая в свою очередь определ. ф-циями
.
Получено уравнение Колмогорова для
функции
по переменным
,
которая в свою очередь определ. ф-циями
.
Получено уравнение Колмогорова для
функции
по переменным
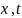 :
:
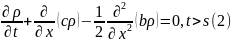
Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
Добавим
к уравн. (2) начальное условие в момент
времени
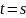 .
Получим задачу Коши, обобщающую задачу
.
Получим задачу Коши, обобщающую задачу
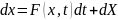 в
в
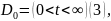
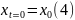 .
.
Задача
Коши для стохастического уравнения.
Требуется определить условную плотность
вероятностей
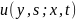 случайного процесса
в момент времени
случайного процесса
в момент времени
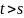 при условии, что случ. процесс
удовлетвор. уравнениям
при условии, что случ. процесс
удовлетвор. уравнениям
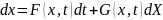 в
в

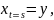 где
где
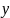 – заданная постоянная величина,
– заданная постоянная величина,
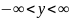 .
.
Определяющая
задача Коши. Требуется
определить условную плотность вероятностей
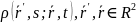 ,
для которой
,
для которой
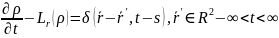 ,
,
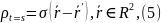 где
оператор
где
оператор
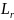 определен в
определен в
 в
в
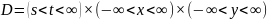 .
При этом должно выполняться условие на
бесконечности
.
При этом должно выполняться условие на
бесконечности
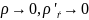 при
при
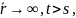 которое обеспечивает условие нормировки
которое обеспечивает условие нормировки
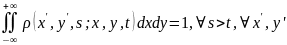
Задача Коши (5) является определяющей дифференциальной задачей для марковского стохастического процесса при условии существования неотрицательного решения задачи.
