
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
Н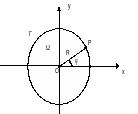 а
плоскости
а
плоскости
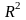 с координатами
с координатами
 рассмотрим круг
рассмотрим круг
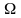 радиуса
радиуса
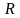 ,
описанный вокруг начала координат
,
описанный вокруг начала координат
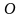 .
Граница круга – окружность
.
Граница круга – окружность
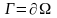 (рис.4.4). Для круга сформулируем внутреннюю
задачу Дирихле для уравнения Лапласа:
(рис.4.4). Для круга сформулируем внутреннюю
задачу Дирихле для уравнения Лапласа:
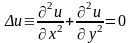 в области
,
(4.34).
в области
,
(4.34).
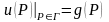 ,(4.35)
,(4.35)
где
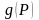 - заданная функция на окружности
- заданная функция на окружности
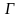 .
.
Рис.
4.4 Требуется
найти решение
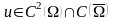 .
.
В
полярных координатах
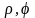 :
:
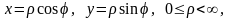
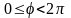 ,
задача (4.34), (4.35) запишется в виде
,
задача (4.34), (4.35) запишется в виде
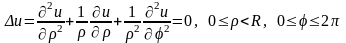 ,
(4.36).
,
(4.36).
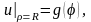
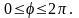 (4.37)
(4.37)
Задачу
(4.36), (4.37) решим методом разделения
переменных в полярных координатах.
Согласно методу разделения переменных,
найдем все решения уравнения Лапласа
(4.36) вида
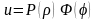 .
(4.38).Подставив
(4.38) в уравнение (4.36), получим равенство
.
(4.38).Подставив
(4.38) в уравнение (4.36), получим равенство
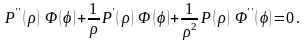 Разделим
это равенство на
Разделим
это равенство на
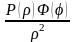 ,
отделяя функции зависящие от
,
отделяя функции зависящие от
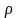 и функции зависящие от
и функции зависящие от
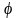 ,
тогда
,
тогда
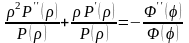 .Выражение
слева зависит только от
,
а выражение справа - только от
,
поэтому это равенство имеет место тогда
и только тогда, когда эти выражения
являются постоянными, то есть
.Выражение
слева зависит только от
,
а выражение справа - только от
,
поэтому это равенство имеет место тогда
и только тогда, когда эти выражения
являются постоянными, то есть
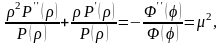 где
где
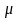 -
постоянная разделения. В результате
получим два обыкновенных дифференциальных
уравнения:
-
постоянная разделения. В результате
получим два обыкновенных дифференциальных
уравнения:
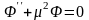 ,
,
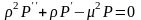 (4.39). Рассмотрим случай, когда
(4.39). Рассмотрим случай, когда
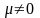 .
Общие решения уравнений (4.39) определяются
формулами
.
Общие решения уравнений (4.39) определяются
формулами
 ,
,
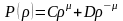 ,
(4.40) где
,
(4.40) где
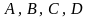 -
произвольные постоянные. Рассмотрим
случай, когда
-
произвольные постоянные. Рассмотрим
случай, когда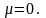 Уравнения (4.39) примут вид
Уравнения (4.39) примут вид
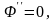
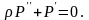 Запишем
общие решения этих уравнений:
Запишем
общие решения этих уравнений:
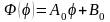 ,
,
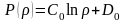 ,
(4.41) где
,
(4.41) где
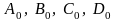 -
произвольные постоянные. После подстановки
функций (4.40), (4.41) в (4.38) получим частные
решения уравнения Лапласа в полярных
координатах:
-
произвольные постоянные. После подстановки
функций (4.40), (4.41) в (4.38) получим частные
решения уравнения Лапласа в полярных
координатах:
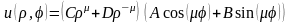 ,
,
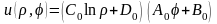 (4.42).
По смыслу задачи (4.36),
(4.37) решение
(4.42).
По смыслу задачи (4.36),
(4.37) решение
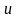 должно быть периодическим по углу
с периодом
должно быть периодическим по углу
с периодом
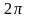 ,
то есть
,
то есть
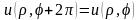 .
Условие периодичности для функций
(4.42) будет выполнено, если
.
Условие периодичности для функций
(4.42) будет выполнено, если
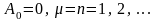 .
В результате получим последовательность
частных периодических решений уравнения
(4.36):
.
В результате получим последовательность
частных периодических решений уравнения
(4.36):
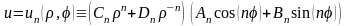 ,
,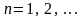
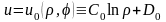 .(4.43)
.(4.43)
Образуем общее решение уравнения (4.36) в виде линейной комбинации частных решений (4.43):
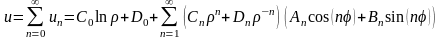 .
.
По
смыслу задачи решение
должно быть ограниченным в центре круга
 .
В связи с этим необходимо положить
.
В связи с этим необходимо положить
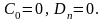 В
результате получим представление
решения задачи (4.36), (4.37) в виде разложения
в ряд
В
результате получим представление
решения задачи (4.36), (4.37) в виде разложения
в ряд
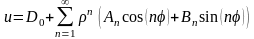 .(4.44)
.(4.44)
Неизвестные
коэффициенты
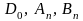 определим из граничного
определим из граничного
условия
(4.37). Подставляя (4.44) в (4.37), получим
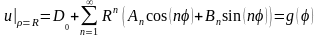 (4.45). Разложим функцию
(4.45). Разложим функцию
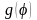 в ряд Фурье
в ряд Фурье
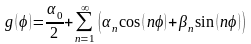 ,
(4.46) где
,
(4.46) где
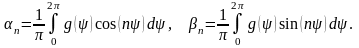 (4.47).
Приравнивая ряды (4.45) и (4.46), вычисляем
коэффициенты
(4.47).
Приравнивая ряды (4.45) и (4.46), вычисляем
коэффициенты
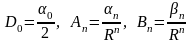 .
.
Подставив
коэффициенты в разложение (4.44), получим
решение исходной задачи Дирихле (4.34),
(4.35):
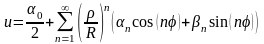 (4.48).
Можно показать, что если граничная
функция
(4.48).
Можно показать, что если граничная
функция
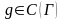 и
и
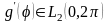 ,
то ряд (4.48) равномерно сходится и
.
Если подставить интегралы (4.47) в (4.48) и
просуммировать ряды, то получим решение
задачи Дирихле для круга в виде интеграла
,
то ряд (4.48) равномерно сходится и
.
Если подставить интегралы (4.47) в (4.48) и
просуммировать ряды, то получим решение
задачи Дирихле для круга в виде интеграла
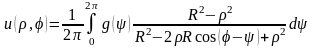 ,
,
называемого интегралом Пуассона.
Аналогично
показывается, что решение внешней задачи
Дирихле для круга в области
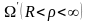 определяется рядом
определяется рядом
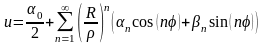 .
.
