
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
Учитывая общую постановку з.Коши, сформулируем з.Коши для ур-ия второго порядка с двумя независимыми переменными, т.е в пр-ве R2:
L(u)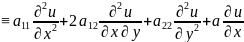 +b
+b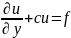 в D,
(1)
в D,
(1)
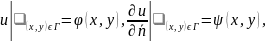 (2)
(2)
где
D-плоская
область в R2;
Г-линия внутри области D,
Г С2;
С2;
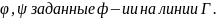
Для
строгой матем.постановки задачи Коши
необходимо ввести след.прост-ва ф-ий:
V1(Г)-прос-ва
начальных ф-ий
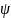 ;
V(D)-прос-во
ф-ий u,
в котором отыскивается решение задачи
Коши. Для классических решений V(D)
;
V(D)-прос-во
ф-ий u,
в котором отыскивается решение задачи
Коши. Для классических решений V(D)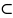 C2(D).
C2(D).
Опр.
З.Коши поставлена корректно в прос-вах
V1,
V2,
V,
если выполнены три условия корректности:
1)для любых нач.ф-ий
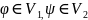 сущ.решение
задачи u
сущ.решение
задачи u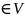 ;
2) для любых нач.ф-ий
решение
единственно в прост-ве V;
3) решение задачи u
непрерывно зависит от начальных ф-ий
.
;
2) для любых нач.ф-ий
решение
единственно в прост-ве V;
3) решение задачи u
непрерывно зависит от начальных ф-ий
.
Если не выполнено хотя бы одно из условий корректности, то задача называется некорректно поставленной. Если же не выполнено третье условие корректности, то задача Коши наз-ся неустойчивой по нач.данным.
Процедура
построения решения задачи Коши для
ур.колебания струны показывает, что
любое классическое решение з.Коши для
ур.колебания струны представимо формулой
Даламбера
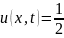 (
(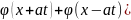 +
+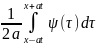 .
Отсюда следует существование и
единственность решения задачи в прос-ве
V.
.
Отсюда следует существование и
единственность решения задачи в прос-ве
V.
Пример Адамара.
На
плоскости R2
рассмотрим эллиптическое ур-ие Лапласа,
для которого поставим з.Коши с нач.усл.
на линии Г(у=0):
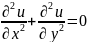 в области D=
в области D=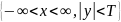 ,
(3)
,
(3)
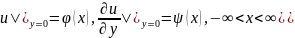 (4).
Ур-ие (3) явл-ся ур-ем типа Ковалевской,
поэтому в случае аналитических ф-ий
(4).
Ур-ие (3) явл-ся ур-ем типа Ковалевской,
поэтому в случае аналитических ф-ий
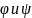 на
основании теоремы Ковалевской заключаем,
что задача (3),(4) имеет единтств.
аналитическое решение в некоторой
достаточно малой окрестности линии Г.
Т.о, первые два условия корректности
выполнены. Исследуем третье условие
корректности, т.е условие о непрерывной
зависимости от начальных ф-ий. Для этого
рассмотрим две задачи Коши с различными
нач.усл. специального вида:
на
основании теоремы Ковалевской заключаем,
что задача (3),(4) имеет единтств.
аналитическое решение в некоторой
достаточно малой окрестности линии Г.
Т.о, первые два условия корректности
выполнены. Исследуем третье условие
корректности, т.е условие о непрерывной
зависимости от начальных ф-ий. Для этого
рассмотрим две задачи Коши с различными
нач.усл. специального вида:
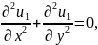
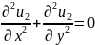
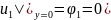 ,
,
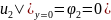 (5)
(5)
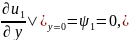
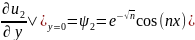
где n-фиксированный положит.параметр.
Решения
данных задач определяются выражениями
u1=0,
u2=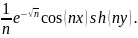 Введем прост-ва ф-ий V1=V2=C0A(R1),
V=
C0A(D),
где C0A-
прос-во ограниченных аналитических
ф-ий.
Введем прост-ва ф-ий V1=V2=C0A(R1),
V=
C0A(D),
где C0A-
прос-во ограниченных аналитических
ф-ий.
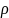 (u1,u2)=
(u1,u2)= <
<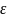 (6)
(6)
Очевидно,
что нер-во (6) не выполнено при дост.
Больших значениях пар-ра n,
т.к.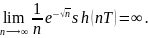 Т.о., з.Коши для эллиптического ур-ия
(3), (4) поставлена некорректно, т.к. не
выполнено третье условие корректности
из определения.
Т.о., з.Коши для эллиптического ур-ия
(3), (4) поставлена некорректно, т.к. не
выполнено третье условие корректности
из определения.
11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
Рассм.
з.Коши для однор. параб. ур-ия с
пост.коэф.: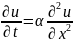 +
+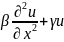 (1)
(1)
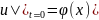 (2).
с нач.усл.(2), где ф-ия
-ограничена
и непрерывна на
(2).
с нач.усл.(2), где ф-ия
-ограничена
и непрерывна на
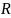 .
Решим з.Коши методом интегральных
преобр.. Применим преобр. Фурье по
аргументу х: U(t)=F[u].
Формально изображение U
зависит не только от аргумента t,
но и переменной
.
Однако эту переменную будем считать
пар-ром и не вкл.ее в число аргументов
ф-ии U.
Используя св-ва преобр. Фурье:
.
Решим з.Коши методом интегральных
преобр.. Применим преобр. Фурье по
аргументу х: U(t)=F[u].
Формально изображение U
зависит не только от аргумента t,
но и переменной
.
Однако эту переменную будем считать
пар-ром и не вкл.ее в число аргументов
ф-ии U.
Используя св-ва преобр. Фурье:
F[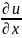 ]=
]=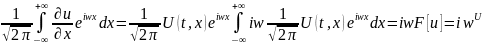
F[
]=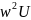
 -образ
ф-ии
.
Тогда преобразованная задача примет
вид:
-образ
ф-ии
.
Тогда преобразованная задача примет
вид:
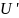 =(
=( )U,
U(0)=
)U,
U(0)=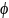 .
Получим з.Коши для обыкн. ДУ с разделяющимися
перем. U(t)=
.
Получим з.Коши для обыкн. ДУ с разделяющимися
перем. U(t)=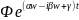 -решение
ДУ. Возвращаясь к з.Коши (1),(2) получим:
u(t,x)=
-решение
ДУ. Возвращаясь к з.Коши (1),(2) получим:
u(t,x)=
G(x,y,t)=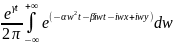 (3)
(3)
Непосредственно вычисляя интеграл, получим:
=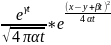
u(t,x)=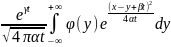 (4)
(4)
ф-ия G, введенная по правилу(3) наз-ся фундамент. решением ур-ия (1). С помощью него, решение з.Коши записывается в виде(4). Аналогично происходит применение интегральных преобразований к другим задачам мат.физики.
