
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
1.Предмет дифференциальных уравнений с частными производными. Историческое развитие исследований уравнений с частными производными, их использование в методах математического моделирования реальности. Современное состояние науки.
При математ. моделировании различных явлений получ-ся ДУ, в кот. входит неизвестная ф-ция, зависящая от многих независимых переменных и, следоват., ур-ние, поскольку оно явл-ся ДУ, содержит частные производные от неизвестной ф-ции. Т.к. почти все физич. явления описыв-ся ДУвЧП, то часто в тех случаях, когда ДУ описывает физич. процесс , эти ур-ния наз-ся ур-ниями мат. физики. Однако надо иметь в виду, что ДУвЧП опис-ся не только физич., но и химич.,биологич. и экономич. процессы и явления. Типичный пример – ур-ние теплопроводности.
Большой вклад в развитие ДУвЧП внесли многие математики мира. Для решения задач ДУвЧП были созданы новые разделы: функциональный анализ, теория обобщенных ф-ций, теория новых функциональных простр-в. Отметим самые известные имена в истории развития ДУвЧП.
И.Г.Петровский положил начало развития общей теории линейных систем в частных производных, а также их классификацию. С.Л.Соболев ввел новое понятие – обобщенное решение дифф. ур-ния; им были введены и изучены новые функциональные пространства.
Исследования в области ДУвЧП идут в двух направлениях. С одной стороны: создается общая теория ДУвЧП, т.е. для общих ур-ний и граничных условий изучаются вопрося существования решений , их единственность и устойчивость. С другой стороны: существует много ДУвЧП, описывающих те или иные физические или биологические явления, решения которых нужно изучить при различных граничных условиях, в том числе изучить качественные свойства этих решений.
2.Основные
понятия об уравнениях с частными
производными. Классические решения
простейших уравнений с частными
производными. Общее решение гиперболических
уравнений второго порядка с двумя
переменными.
Рассмотр.
n-мерное
евклидово простр-во
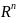 если x
если x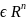 ,
то она имеет координаты x=x(x1,…,xn).
Пусть
,
то она имеет координаты x=x(x1,…,xn).
Пусть
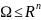 .
В этой обл. рассмотрим ф-цию u=u(x)=u(x1,
…xn).
.
В этой обл. рассмотрим ф-цию u=u(x)=u(x1,
…xn).
Опр.
Множ-во ф-ций
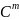 (
(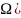 наз-ся
простр-вом m
раз непрер-диффер ф-ций на обл Ω, т.е. u
наз-ся
простр-вом m
раз непрер-диффер ф-ций на обл Ω, т.е. u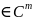 (
,
то это значит, что на обл.Ω сама ф-ция
определена и непрерывна, а также существ
и непрер все её частные производн на
обл Ω до порядка n
включительно.В случае m=
(
,
то это значит, что на обл.Ω сама ф-ция
определена и непрерывна, а также существ
и непрер все её частные производн на
обл Ω до порядка n
включительно.В случае m=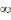 имеем простр-во любое число раз
непрер-диффер ф-ций.
имеем простр-во любое число раз
непрер-диффер ф-ций.
Рассмотр
произв ф-цию F(x1,..,xn,z1,…,zn)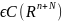 .Будем
предполагать, что существ и непрер частн
производн:
.Будем
предполагать, что существ и непрер частн
производн: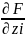 ≠0.
≠0.
Опр.Диффер
ур-нием с частн производн относит ф-ции
u=u(x)
будем назыв рав-во: F(x,u,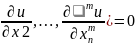 .(1)
.(1)
C помощью ф-ции F введем диффер оператор L он действует на ф-цию u:
L[u]=
F(x,u,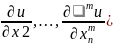 .Т.о.
в результате действия оператора L
на ф-цию u
получаем непрерывную ф-цию.Тогда ур-ние
(1)можем записать в виде: L[u]=0.
.Т.о.
в результате действия оператора L
на ф-цию u
получаем непрерывную ф-цию.Тогда ур-ние
(1)можем записать в виде: L[u]=0.
Опр.Классическим решением ур-ния(1)на обл Ω назыв такую ф-цию u ( , кот при подстановке в рав-во (1) обращает его в верное тождество.
Из
записи (1)
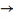 что
в ур-ние (1) входит производная со старшим
порядком m.
Поэтому будем говорить, что порядок
ур-ния равен m,
или степень оператора L
равна m.
что
в ур-ние (1) входит производная со старшим
порядком m.
Поэтому будем говорить, что порядок
ур-ния равен m,
или степень оператора L
равна m.
Ур-ние (1) иногда можно записать в виде: L[u]=f(x).Такое ур-ние назывюлинейным ур-нием с частнами производнами, если для оператора L выполнены условия линейности:
L[αu]=αL[u],
α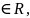 u
(
(2)
u
(
(2)
L[u1+u2]=L[u1]+L[u2] (3)
Утвержд.Любое линейн ур-ние с частн производн порядка m имеет вид:
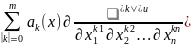 =f(x)
(4)
=f(x)
(4)
Т.е.L[u]=
,
k-мультииндекс с координ k=(k1,k2,…,kn);
|k|=k1+k1+…+kn.

Если в ур-нии (4) ф-ция f(x)=0, то такое ур-ние наз-ся однородным, в противн случ неоднородным.
3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
L[u]=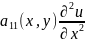 +
+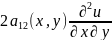 +
+ +
+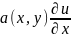 +
+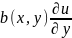 +c(x,y)u=f(x,y)
(6)
+c(x,y)u=f(x,y)
(6)
Для
классификации ур-ний введем в рассмотрение
вспомогат ф-цию:D(x,y)= -
-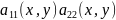 -дискриминант
ур-ния (6).
-дискриминант
ур-ния (6).
Опр. В зависимости от дискриминанта ур-ние (6) наз-ся:
1)гиперболическим
в т.(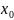 ,
,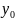 )
)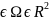 ,
если D(
,
,
если D(
,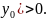
2)параболическим
в т.(
,
)
,
если D(
,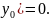
3)
эллиптическим в т.(
,
)
,
если D(
,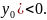
Графически
ур-ние D(
,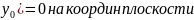 определ некот кривую l,кот
может делить обл Ω на 2 подобл
определ некот кривую l,кот
может делить обл Ω на 2 подобл
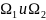 ,
где D>0
и D<0
соотв, тогда на
,
где D>0
и D<0
соотв, тогда на
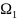 ур-ние (6) гиперболич типа, на
ур-ние (6) гиперболич типа, на
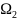 -
эллиптич типа, на l
–параболич типа.В этом случае будем
говорить, что на всей обл Ω ур-ние (6)
смешанного типа. Тогда обл
-
эллиптич типа, на l
–параболич типа.В этом случае будем
говорить, что на всей обл Ω ур-ние (6)
смешанного типа. Тогда обл
 -
обл эллиптичности , линия l-линияпараболичности.
-
обл эллиптичности , линия l-линияпараболичности.
Пример: 1)ур-ние колебаний струны:
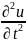 -
-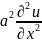 =f(t,x)
=f(t,x)
2)одномерное ур-ние теплопроводности:
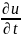 -
=f(t,x)
-
=f(t,x)
3)ур-ние Пуассона:
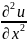 +
+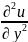 =f(t,x)
=f(t,x)
Системы.
Рассмотр kнеизвестных
ф-ций
 ,
,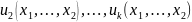 и k
вспомогательных ф-ций
и k
вспомогательных ф-ций
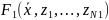 ,…,
,…,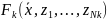 ,обладающих
св-вами аналогичными св-вам ф-ции F.
,обладающих
св-вами аналогичными св-вам ф-ции F.
Опр.
Системой ДУ с частными производными
относит kнеизвестных
ф-ций
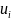 (i=1,2,…,k)
наз-ся k
ур-ний:
(i=1,2,…,k)
наз-ся k
ур-ний:
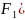 )=0
)=0
… (1.9)
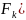 )=0
)=0
Сис-ма ур-ний (1,9) линейная, если
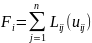 ,
где
,
где
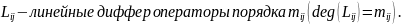
Классификация систем проводится аналогично как классификация уравнений.
4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
L[u]
=
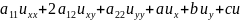 =f
(6)
=f
(6)
Будем
считать, что ур-ние(6) имеет достаточно
гладкие коэф. Поставим задачу об упрощении
ур-ния(6) с помощью замены переменных.
Введём новые независимые перемен.
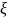 и η:
и η:
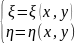 (9)
(9)
Будем считать, что преобразование (9) невырожденное, т.е. якобиан перехода отличен от нуля:
I
=
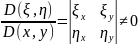 ,
,
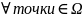
grad
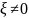 ,
grad
,
grad
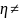 0.
Выразим производ. по старым перемен.
ч/з производ. по новым перемен.
0.
Выразим производ. по старым перемен.
ч/з производ. по новым перемен.
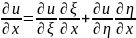
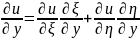
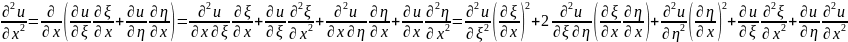

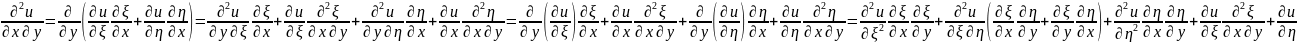
Подставим
получ. знач. произод. в ур-ние(6). После
приведения подобных в новых независимых
перемен.
и
 ур-ние (6) примет вид:
ур-ние (6) примет вид:
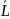 [u]
=
[u]
=
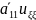 +2
+2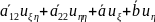 +
+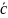 u=
u=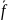 (11)
(11)
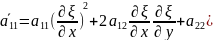
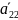 =
=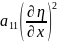 +2
+2 (12)
(12)
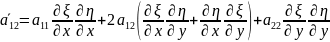
Утверждение
2.
При невырожденном преобраз. (9) тип ур-ния
(6) сохраняется. Д-во:
справедливость вытекает из того, что
дискрименант нового ур-ния (11)
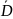 =
=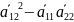 =
= ,
D
– дискрименант ур-ния(6). Значит сравнения
с нулём дисерим. D
и
совпадают.
,
D
– дискрименант ур-ния(6). Значит сравнения
с нулём дисерим. D
и
совпадают.
Выберем замену(9) так, чтобы преобразованное ур-ние(11) имело более простой вид. С решением этой задачи тесно связано обыкновенное дифферен. ур-ние:
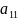 (x,y)
(x,y)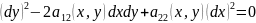 (13) – характеристическое
ур-ние(6) или ур-ние характеристик.
(13) – характеристическое
ур-ние(6) или ур-ние характеристик.
Разрешая
ур-ние(13) получаем:
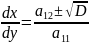
Ур-ние(13) часто называют ур-нием характеристик в дифференциалах. С этим ур-нием тесно связано нелинейное диф. ур-ние 1-го порядка с частными производ.
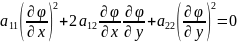 (14),
(14),
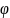 – неизвестная ф-ция. Ур-ние(14) также
наз-ся ур-нием
характеристик или ур-нием характеристик
в частных производ.
Если удаётся найти 2 лин.-независимых
решения ур-ния характеристик(13) или (14)
то тем самым будет найдено невырожденное
преобразов.(9) кот упрощает вид ур-ния(11).
Из курса обыкновенных диф. ур-ний
известно, что у обыкновен. диф. ур-ния(12)
сущ. 2 линейно-независим. решения если
D>0,
одно независим. решение, если D=0
и комплекснозначное решение если D<0.
Поскольку коэф.
,
– неизвестная ф-ция. Ур-ние(14) также
наз-ся ур-нием
характеристик или ур-нием характеристик
в частных производ.
Если удаётся найти 2 лин.-независимых
решения ур-ния характеристик(13) или (14)
то тем самым будет найдено невырожденное
преобразов.(9) кот упрощает вид ур-ния(11).
Из курса обыкновенных диф. ур-ний
известно, что у обыкновен. диф. ур-ния(12)
сущ. 2 линейно-независим. решения если
D>0,
одно независим. решение, если D=0
и комплекснозначное решение если D<0.
Поскольку коэф.
,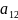 ,
,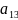 действительны, то их действ. и мнимая
части этого комплекснозначного решения
будут решениями(ЛНЗ) ур-ния в частных
производ.(14).
действительны, то их действ. и мнимая
части этого комплекснозначного решения
будут решениями(ЛНЗ) ур-ния в частных
производ.(14).
