
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
29 Постановка задач для уравнения денежных накоплений
Как
было показано, если динамика денежных
и материальных накоплений отдельной
семьи подчиняется системе стохастических
уравнений (6.39), где
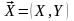 –
марковский стохастический процесс с
переходной функцией плотности вероятностей
–
марковский стохастический процесс с
переходной функцией плотности вероятностей
 ,
которая определяется функциями
,
которая определяется функциями
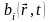 ,
,
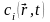 ,
,
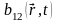 (5.20), тогда плотность
(5.20), тогда плотность
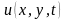 ансамбля семей в пространстве накоплений
N
ансамбля семей в пространстве накоплений
N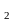 удовлетворяет
параболическому уравнению (6.54):
удовлетворяет
параболическому уравнению (6.54):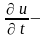
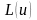
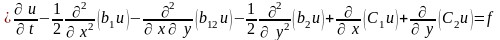 ,
(6.80)где
,
(6.80)где
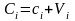 ;
–
эллиптический оператор. Из множества
решений уравнения (6.80) необходимо найти
единственное решение, которое адекватно
описывает динамику накоплений выделенного
множества семей (ансамбля семей), схожих
по своей экономической деятельности.
Для выделения единственного решения
на искомую функцию
необходимо наложить дополнительные
условия, порождающие краевую задачу.
Сформулируем некоторые краевые задачи
для уравнения (6.80) по аналогии с краевыми
задачами для двухмерного уравнения
теплопроводности (3.26).Задача
Коши на пространстве накоплений
N
.
Предположим, что в начальный момент
времени
;
–
эллиптический оператор. Из множества
решений уравнения (6.80) необходимо найти
единственное решение, которое адекватно
описывает динамику накоплений выделенного
множества семей (ансамбля семей), схожих
по своей экономической деятельности.
Для выделения единственного решения
на искомую функцию
необходимо наложить дополнительные
условия, порождающие краевую задачу.
Сформулируем некоторые краевые задачи
для уравнения (6.80) по аналогии с краевыми
задачами для двухмерного уравнения
теплопроводности (3.26).Задача
Коши на пространстве накоплений
N
.
Предположим, что в начальный момент
времени
 известны накопления каждой семьи. В
результате с помощью соотношения (6.40)
можно определить функцию плотности
распределения семей
известны накопления каждой семьи. В
результате с помощью соотношения (6.40)
можно определить функцию плотности
распределения семей
 на пространстве накоплений N
в начальный момент времени. Получим
начальное условие
на пространстве накоплений N
в начальный момент времени. Получим
начальное условие
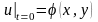 .
(6.81)Добавив начальное условие (6.81) к
уравнению (6.80), поставим задачу Коши
.
(6.81)Добавив начальное условие (6.81) к
уравнению (6.80), поставим задачу Коши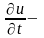
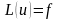 в
в
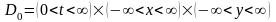 ,
(6.82)
,
,
(6.82)
,
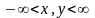 ,
(6.83) в которой требуется определить
решение
,
(6.83) в которой требуется определить
решение
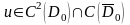 уравнения (6.82), удовлетворяющее условию
(6.83).Смешанные
задачи с нелокальными граничными
условиями. Разобьем
отрезок
уравнения (6.82), удовлетворяющее условию
(6.83).Смешанные
задачи с нелокальными граничными
условиями. Разобьем
отрезок
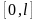 на элементарные отрезки
на элементарные отрезки
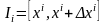 длиной
длиной
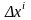 .
В соответствии с формулой (6.16) на отрезке
.
В соответствии с формулой (6.16) на отрезке
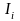 находится
находится
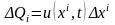 семей. Так как каждая семья на отрезке
имеет приблизительно
семей. Так как каждая семья на отрезке
имеет приблизительно
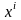 рублей накоплений, то в семьях на отрезке
сосредоточено
рублей накоплений, то в семьях на отрезке
сосредоточено
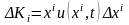 рублей. Суммируя по всем элементарным
отрезкам, вычисляем сумму денег:
рублей. Суммируя по всем элементарным
отрезкам, вычисляем сумму денег:
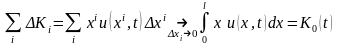 ,
(6.72) где
,
(6.72) где
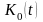 – сумма денег, накопленных в семьях на
отрезке
в момент времени
– сумма денег, накопленных в семьях на
отрезке
в момент времени
 .
Поставим смешанную краевую задачу для
уравнения денежных накоплений (6.56) на
пространстве накоплений N
.
Поставим смешанную краевую задачу для
уравнения денежных накоплений (6.56) на
пространстве накоплений N с граничным условием (6.60) и специальным
условием (6.72):
с граничным условием (6.60) и специальным
условием (6.72):
 в
в
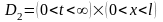 ,
,
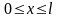 ,
,
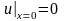 ,
,
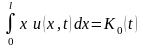 ,
,
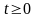 ,
(6.73) где второе условие (6.73) называется
нелокальным
граничным условием,
так как в нем задействовано не только
значение функции
в изолированной точке
,
(6.73) где второе условие (6.73) называется
нелокальным
граничным условием,
так как в нем задействовано не только
значение функции
в изолированной точке
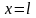 ,
но и значения искомой функции
во всех точках отрезка
.
Если вместо первого условия (6.73) задано
число семей
,
но и значения искомой функции
во всех точках отрезка
.
Если вместо первого условия (6.73) задано
число семей
 в ансамбле на пространстве N
в соответствии с формулой (6.17), тогда
имеем задачу с двумя нелокальными
граничными условиями:
в
,
,
,
в ансамбле на пространстве N
в соответствии с формулой (6.17), тогда
имеем задачу с двумя нелокальными
граничными условиями:
в
,
,
,
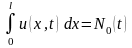 ,
,
.
(6.74) Заметим, что сформулированные
краевые задачи требуют исследования
проблемы существования и единственности
решения при дополнительном условии
положительности решения.
,
,
.
(6.74) Заметим, что сформулированные
краевые задачи требуют исследования
проблемы существования и единственности
решения при дополнительном условии
положительности решения.
28 Параболические уравнения Колмогорова
Одномерные
уравнения Колмогорова. Рассмотрим
марковский стохастический процесс c
переходной функцией плотности вероятностей
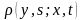 .
Выведем два уравнения с частными
производными, которым удовлетворяет
переходная функция по двум парам
переменных, соответственно по
.
Выведем два уравнения с частными
производными, которым удовлетворяет
переходная функция по двум парам
переменных, соответственно по
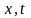 и по
и по
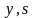 .
Вывод
уравнений оформим в виде двух теорем.
.
Вывод
уравнений оформим в виде двух теорем.
Теорема 5.1. Пусть:
для переходной функции плотности вероятностей выполнены свойства А;
плотность при фиксированных и
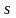
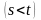 ограничена, то есть
ограничена, то есть
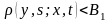 ,
где
,
где
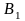 не зависит от
и
не зависит от
и
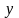 ;
;функции

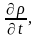
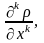
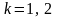 ,
непрерывны, как функции двух переменных
и
на множестве
,
непрерывны, как функции двух переменных
и
на множестве
 ;
;

производные
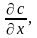
 ,
непрерывны на множестве
,
непрерывны на множестве
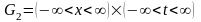 .
.
Тогда
плотность
удовлетворяет параболическому уравнению
с частными производными по переменным
,
на
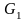 :
:

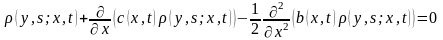 .
.
Постановка
задач для уравнения денежных накоплений
ансамбля семей.
Как было ранее показано, если динамика
денежных накоплений отдельной семьи
подчиняется стохастическому уравнению
(6.13), где
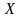 - марковский стохастический процесс с
переходной функцией пло-тности
вероятностей
,
которая определяется функциями
- марковский стохастический процесс с
переходной функцией пло-тности
вероятностей
,
которая определяется функциями
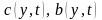 (5.10), тогда плотность
(5.10), тогда плотность
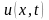 ансамбля семей в пространстве накоплений
N
ансамбля семей в пространстве накоплений
N удовлетворяет
параболическому уравнению (6.30):
удовлетворяет
параболическому уравнению (6.30):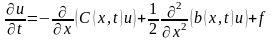 ,
(6.56),где
,
(6.56),где
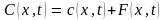 .
Из множества решений уравнения (6.56)
необходимо найти единственное решение,
которое адекватно описывает динамику
накоплений выделенного множества семей,
схожих по своей экономической деятельности.
Для выделения единственного решения
на искомую функцию
необходимо наложить некоторые
дополнительные условия, возникающие в
зависимости от дополнительной информации,
которой обладает исследователь.
Сформулируем краевые задачи для уравнения
(6.56) по аналогии с краевыми задачами
математической физики.
.
Из множества решений уравнения (6.56)
необходимо найти единственное решение,
которое адекватно описывает динамику
накоплений выделенного множества семей,
схожих по своей экономической деятельности.
Для выделения единственного решения
на искомую функцию
необходимо наложить некоторые
дополнительные условия, возникающие в
зависимости от дополнительной информации,
которой обладает исследователь.
Сформулируем краевые задачи для уравнения
(6.56) по аналогии с краевыми задачами
математической физики.
7.Приведение
к каноническому виду уравнений второго
порядка с постоянными коэффициентами.
Исключение младших производных в
уравнениях. Уравнение
характеристик.
Рассмотрим класс линейных уравнений
второго порядка с
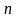 независимыми переменными:
независимыми переменными:
 ,
(1)
,
(1)
где
коэффициенты
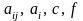 определены в области
определены в области
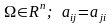 .Выделим
главную часть уравнения
.Выделим
главную часть уравнения
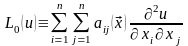 .
(2) Рассмотрим
числовых переменных
.
(2) Рассмотрим
числовых переменных
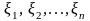 и поставим в соответствие производным
функции
числовые выражения по следующему правилу
и поставим в соответствие производным
функции
числовые выражения по следующему правилу
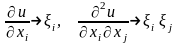 ,(3)
тогда главной части (3) соответствует
полином по переменным
:
,(3)
тогда главной части (3) соответствует
полином по переменным
:
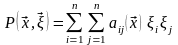 .
(4) Полином (4) по
переменным
.
(4) Полином (4) по
переменным
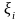 называется характеристическим
полиномом.
Зафиксируем точку
называется характеристическим
полиномом.
Зафиксируем точку
 ,
получим квадратичную форму с постоянными
коэффициентами
,
получим квадратичную форму с постоянными
коэффициентами
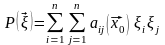 .
(5) Рассмотрим поверхность
,
принадлежащую области
,
которую зададим уравнением
.
(5) Рассмотрим поверхность
,
принадлежащую области
,
которую зададим уравнением
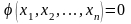 ,(6),
где
,(6),
где
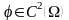 .
.
Опр.Поверхность , заданная уравнением (6), называется характеристикой или характеристической поверхностью уравнения (1), если во всех точках поверхности функции удовлетворяет ур.
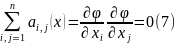
Уравнение (7) называется уравнением характеристик
Приведение к каноническому виду уравнений с постоянными коэффициентами. Рассмотрим уравнение (1) с постоянными коэффициентами
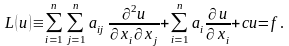 (8)
(8)
Приведем
его к каноническому виду с помощью
замены независимых переменных. Для
этого в уравнении (8) перейдем от переменных
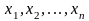 к новым переменным
к новым переменным
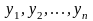 ,
производя замену
,
производя замену
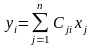 ,
(9) Причем преобразование (9)
не вырожденное det(
,
(9) Причем преобразование (9)
не вырожденное det( )
)
Вычислим производные
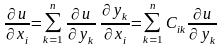 ,
,
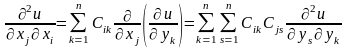 .
.
После подстановки в (8) получим уравнение в новых переменных:
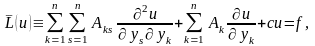
где
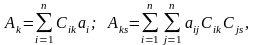 , тогда уравнение (8) с помощью преобразования
(9) приводится к каноническому виду
, тогда уравнение (8) с помощью преобразования
(9) приводится к каноническому виду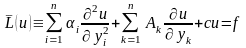 .
.
8.Постановка
задачи Коши. Теорема Коши-Ковалевской.
Рассмотрим
-мерное
евклидово пространство
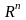 .
Пусть
.
Пусть
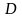 -
связная область в пространстве
,
точка
-
связная область в пространстве
,
точка
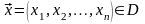 .
В области
зададим уравнение с частными производными
второго порядка
.
В области
зададим уравнение с частными производными
второго порядка
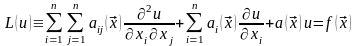 (1)
(1)
с
достаточно гладкими коэффициентами.
Тип уравнения (1) может быть любым. В
пространстве
зададим незамкнутую без самопересечений
поверхность
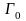 с помощью уравнения
с помощью уравнения
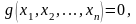 (2) где функция
(2) где функция
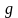 является дважды непрерывно дифференцируемой
функцией, то есть
является дважды непрерывно дифференцируемой
функцией, то есть
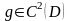 ,
а
,
а
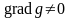 в любой точке
в любой точке
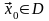 .
О
.
О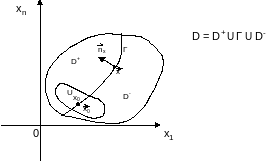 бозначим
через
бозначим
через
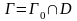 часть поверхности, лежащей внутри
области
.
Будем предполагать, что область
представима в виде
часть поверхности, лежащей внутри
области
.
Будем предполагать, что область
представима в виде
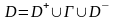 ,
где
,
где
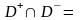 0
,
а подобласти
0
,
а подобласти
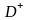 ,
,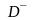 не имеют общих точек с поверхностью
(см.
рис. 1).
не имеют общих точек с поверхностью
(см.
рис. 1).
На
поверхности
зададим два условия на неизвестную
функцию
: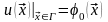 ,
,
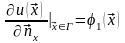 ,
(3) где
,
(3) где
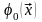 ,
,
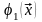 - заданные функции на поверхности
;
- заданные функции на поверхности
;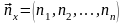 - единичная нормаль к поверхности
в точке
- единичная нормаль к поверхности
в точке
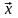 ;
;
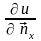 - производная по направлению нормали
- производная по направлению нормали
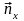 ,
которая определяется выражением
,
которая определяется выражением
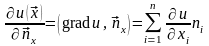 ,
,
 .
(4)
.
(4)
Условия (3) называются начальными условиями.
Задача Коши 1( классическая постановка)
в области , (5)
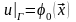 ,
,
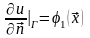 .
(6)
.
(6)
Требуется найти функцию , которая удовлетворяет уравнению (5) в области и начальным условиям (6) на поверхности . Функция , которая удовлетворяет указанным требованиям, называется классическим решением задачи Коши.
Теорема
Ковалевской. Если
коэффициенты уравнения (*)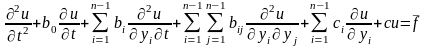 и
нач. фу-ии (**)
и
нач. фу-ии (**)
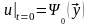
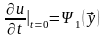 ,
являются аналитическими функциями,
тогда для любой точки y0
кривой
Г(t-0)
существует окрестность этой точки,
целиком лежащей в обл.
в кот. реш. з.Коши (*), (**) единственной в
пространстве аналитических функций.
,
являются аналитическими функциями,
тогда для любой точки y0
кривой
Г(t-0)
существует окрестность этой точки,
целиком лежащей в обл.
в кот. реш. з.Коши (*), (**) единственной в
пространстве аналитических функций.
