
- •3.Классификация уравнений второго порядка с двумя независимыми переменными. Системы уравнений с частными производными.
- •4. Замена независимых переменных в уравнениях второго порядка. Уравнение характеристик.
- •5.Приведение к каноническому виду уравнений второго порядка с двумя независимыми переменными.
- •6.Классификация уравнений второго порядка со многими независимыми переменными.
- •10.Корректно поставленные задачи. Корректность задачи Коши для уравнения колебаний струны. Пример Адамара некорректно поставленной задачи Коши.
- •11. Метод интегральных преобразований для решения задачи Коши для параболических уравнений.
- •12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
- •13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
- •14. Сингулярные обобщенные функции, -функция Дирака. Обобщенная производная, обобщенные решения уравнений с частными производными.
- •15.Фундаментальное решение уравнений. Фундаментальное решение и решение задачи Коши для уравнения Колмогорова.
- •25. Метод разделения переменных для решения задачи Дирихле в круге. Интеграл Пуассона.
- •Формулы Грина для оператора Лапласа. Интегральная ф-ула Грина для гармонических функций.
- •Свойства гармонических ф-ций. Принцип максимума и минимума для гармонических ф-ций, следствия.
- •Краевые задачи Дирихле,Неймана и 3го рода для элиптческих ур-ний.Спектральная задача для оператора Лапласа.Корректность внутрих и внешнх краевых задач для ур-ия Лапласа и Пуассона
- •33. Моделирование динамики стоимости ценных бумаг с помощью стохастических дифференциальных уравнений
- •32. Замена переменных в уравнениях Колмогорова. Формула дифференцирования Ито
- •Вышеизложенное позволяет сформулировать следующее утверждение.
- •31.Связь задачи Коши для стохастического уравнения с задачей Коши для уравн. Колмогорова.
- •Это означает, что марковский стохастический процесс описывается уравнением параболического типа (2).
- •29 Постановка задач для уравнения денежных накоплений
- •28 Параболические уравнения Колмогорова
- •35. Уравнение Блэка - Шоулса, смешанная задача для функции стоимости опциона.
- •16. Постановка смешанных задач для уравнения колебаний струны. Граничные условия первого, второго и третьего рода, физическая интерпретация.
- •17. Задача ш. – л. Для обыкновенных д у 2 порядка. Свойства собственных функций и собственных значений задачи Штурма - Лиувилля.
- •30. Решение задачи Коши для уравнения денежных накоплений. Стохастические дифференциальные уравнения в форме Ито.
- •26.Динамические моделир. Ден. Накоплений семьи с использ. Стохастических ду.
- •27. Одном-е марковские стохаст-е процессы в моделир-и случ. Денежных накоп-й. Условная плотность вероятностей стохас-го процесса и ее свойства.
- •19.Постановка смешанных задач для уравнения теплопроводности в стержне.
- •20. Решение первой смешанной задачи для уравнения теплопроводности в стержне, обоснование решения. Корректность первой смешанной задачи
- •21.Уравнение Лапласа. Гармонические функции. Фундаментальное решение для уравнения Лапласа.
12.Принцип максимума и минимума для уравнения теплопроводности, следствия. Корректность задачи Коши для уравнения теплопроводности.
Рассм.
плос-ть Oxt
и на ней открытый прямоугольник П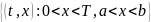 .
Часть границы прямоуг.П обозн.
.
Часть границы прямоуг.П обозн.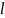 :
=EA
:
=EA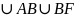
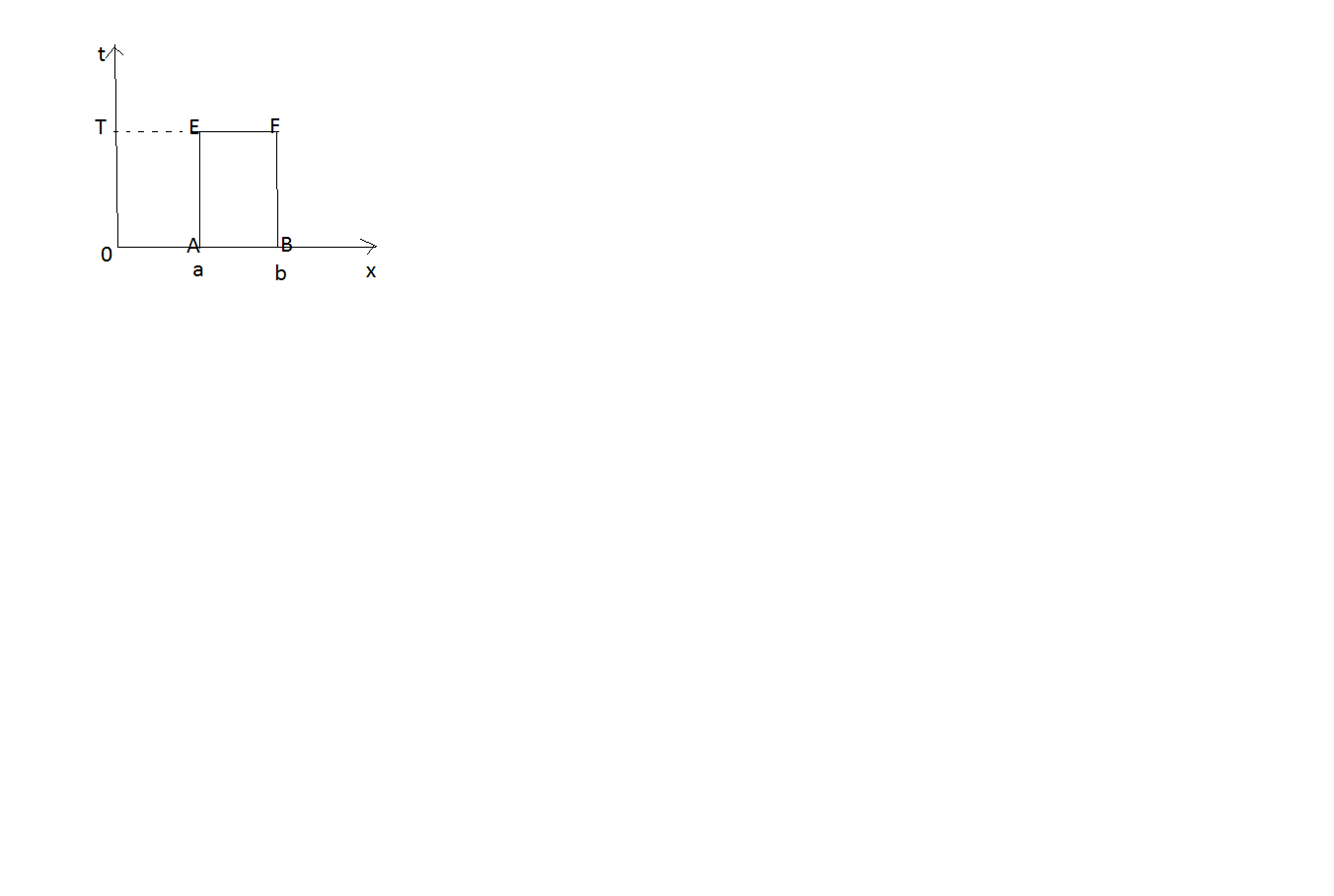
Обозначим
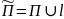 (прямоугольник
+часть его границы). На прямоугольнике
(прямоугольник
+часть его границы). На прямоугольнике
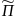 рассм.ур-ие теплопроводности
рассм.ур-ие теплопроводности
 (1)
(1)
Решения ур-ия(1) на не могут принимать сколь угодно больших и сколь угодно малых решений, а именно справедлива теорема (принцип max и min).
Теорема:
Пусть ф-ия U(t,x)
C2(
)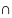 C(
C(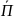 )
и удовл. ур-ию (1) на
,
тогда ф-ия u
достигает своего наиб. и наим. значений
на кривой
.
)
и удовл. ур-ию (1) на
,
тогда ф-ия u
достигает своего наиб. и наим. значений
на кривой
.
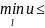 u(t,x)
u(t,x)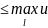
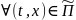 (2)
(2)
Д-во: (проведем для max, для min такле же (замена u=-u) методом от противного)
Предположим,
что
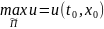 достигается в некот.точке
достигается в некот.точке
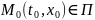 ,
тогда
,
тогда

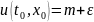 ,
,

Введем
в рассмотрение ф-ию
 (3)
(3)
k=const,
0 .
Значение
.
Значение
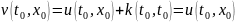 =
=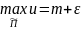 .
.

Получим
знач.ф-ии
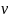 во внутр. точке прямоугольника больше,
чем значения ф-ии на кривой
во внутр. точке прямоугольника больше,
чем значения ф-ии на кривой
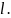 Предположим, что ф-ия
приним. свое наиб. значение в некот.
точке
Предположим, что ф-ия
приним. свое наиб. значение в некот.
точке
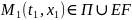 .
Рассм. возможные случаи:
.
Рассм. возможные случаи:
1).точка
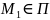 ,
тогда она внутренняя, и согласно
достаточному признаку экстремума для
внутр.точки максимума следует, что
,
тогда она внутренняя, и согласно
достаточному признаку экстремума для
внутр.точки максимума следует, что
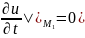
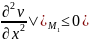 (4)
(4)
2).
Если
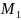 лежит
на стороне
лежит
на стороне
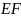 ,
то она граничная для П. Исходя из условия
экстремума (max-мума)
для граничной точки, получаем:
,
то она граничная для П. Исходя из условия
экстремума (max-мума)
для граничной точки, получаем:
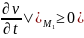 (5)
(5)
Оценим производную ф-ии u:
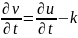 ,
тогда
,
тогда
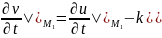 и исходя из (4) и(5):
и исходя из (4) и(5):
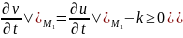 ,
,
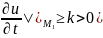 ,
,
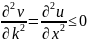
По
условию, ф-ия
 в точке
удовл. условию ур-ия (1). Получим
противоречие, чтд.
в точке
удовл. условию ур-ия (1). Получим
противоречие, чтд.
Следствие1:
Пусть
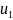 и
и
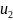 -решение
ур-ия (1) на прямоугольнике
,
тогда
-решение
ур-ия (1) на прямоугольнике
,
тогда
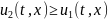
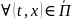 .
.
Следствие2:
Если 3 решения ур-ия (1) на кривой удовл. двойному нер-ву
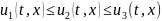
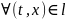 ,
то
,
то
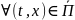 ,
,
13. Пространство осн. Ф-й. Обобщенные ф-и и их сво-ва.
Пусть
x
– вектор пространства
,
x
.
На нем зададим финитную функцию
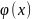 ,
т.е. фун-ю, для кот.сущ.-т. Открытое
ограниченное множество U
,
для кот.
,
т.е. фун-ю, для кот.сущ.-т. Открытое
ограниченное множество U
,
для кот.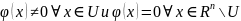 .
Замкнутое множество
.
Замкнутое множество
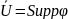 -носитель
финитной функции
.
Множество всех финитных функций является
линейным пространством, которое
обозначается D(
-носитель
финитной функции
.
Множество всех финитных функций является
линейным пространством, которое
обозначается D(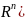 .
Рассмотрим
.
Рассмотрим
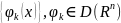 .
.
Опр.
Последоват-ть
 называется сходящейся к финитной функции
,
т.е.
называется сходящейся к финитной функции
,
т.е.
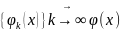 ,
если выполнены условия:1)
,
если выполнены условия:1)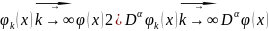 3) существуют ограниченное замкнутое
множество
3) существуют ограниченное замкнутое
множество
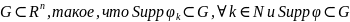 .
.
Про-во
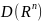 с указанной сходимостью будем называть
пространством основных функций. На этом
пространстве введем линейный функционал
с указанной сходимостью будем называть
пространством основных функций. На этом
пространстве введем линейный функционал
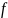 ,
где
,
где
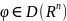 .
.
Линейный
функционал
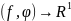 ,
значит, что
,
значит, что
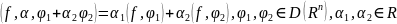 .(1)
.(1)
Опр.Обобщенной функцией будем называть линейный непрерывный функционал на пространстве функций.
Непрерывный
функционал означает, что для любой
последовательности функций
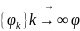 выполнены условия
выполнены условия
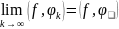 .(2)
.(2)
Исходя
из (1) и (2) можем утверждать, что множество
всех обобщенных функций образует
линейное пространство, которое обозначим
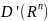 .
.
Рассмотрим
произв. локально суммируемую функцию
g(x),
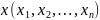 .
С помощью «обычной» функции построим
лин.функционал g
.
С помощью «обычной» функции построим
лин.функционал g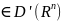 .
Определив его следующим образом
.
Определив его следующим образом
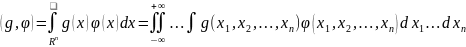 .
Линейный функционал вытекает из свойства
линейности определения n-мерного
интеграла Римана, а непрерывн.из
рассуждений.
.
Линейный функционал вытекает из свойства
линейности определения n-мерного
интеграла Римана, а непрерывн.из
рассуждений.
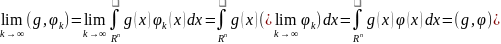 .
.
Т.о. по обычной функции g мы построили функционал g, который является обобщенной функцией. Значит функцию g мы можем рассм.как обобщенную функцию. Такие обобщенные функции будем называть регулярными обобщенными функциями. Все остальные обобщенные функции – сингулярными.
