
- •Дифференциальное исчисление
- •Содержание
- •Введение
- •Задачи для самостоятельного решения
- •Свойства бесконечно малых и бесконечно больших функций
- •Теоремы о пределах (правила предельного перехода)
- •Замечательные пределы. Сравнение бесконечно малых величин
- •Задачи для самостоятельного решения
- •Свойства эквивалентных бесконечно малых функций
- •Важнейшие эквивалентности
- •Задачи для самостоятельного решения
- •3. Практическое занятие по теме: Непрерывность функции. Точки разрыва и их классификация
- •Задачи для самостоятельного решения
- •4. Практическое занятие по теме: вычисление производной функции одной переменной. Таблица производных. Нахождение частных производных. Производная сложной функции
- •Правила дифференцирования результатов арифметических действий над функциями
- •Геометрический смысл производной функции одной переменной
- •Геометрический смысл частных производных функции двух переменных
- •Задачи для самостоятельного решения
- •5. Практическое занятие по теме: производная неявной функции однОй и нескольких переменных. Производная функции, заданной параметрически. Логарифмическое дифференцирование
- •Производная неявно заданной функции.
- •Производная функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Задачи для самостоятельного решения
- •6. Практическое занятие по теме: Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков
- •Основные свойства дифференциала
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •7. Практическое занятие по теме: Правило Лопиталя
- •1.Неопределенность
- •2.Неопределенность .
- •3.Неопределенности , , .
- •Задачи для самостоятельного решения
- •8. Практическое занятие по теме: Общая схема исследования функции и построение графика
- •Алгоритм исследования функции
- •Задачи для самостоятельного решения
- •Библиографический список
Геометрический смысл частных производных функции двух переменных
![]() ,
,
![]() , (4.8)
, (4.8)
где
![]() ‑ угол между осью
‑ угол между осью
![]() и касательной
и касательной
![]() ,
проведенной к линии пересечения
поверхности
,
проведенной к линии пересечения
поверхности
![]() с плоскостью
с плоскостью
![]() ,
в точке
,
в точке
![]() .
.
![]()
 ‑ угол между
осью
‑ угол между
осью
![]() и касательной
и касательной
![]() ,
проведенной к линии пересечения
поверхности
,
проведенной к линии пересечения
поверхности
![]() с плоскостью
с плоскостью
![]() ,
в точке
,
в точке
![]() ;
(см. рис.4.2).
;
(см. рис.4.2).
П лоскость
лоскость
![]() ‑ касательная плоскость к поверхности
‑ касательная плоскость к поверхности
![]() ,
прямая
,
прямая
![]() ‑ нормаль к поверхности
‑ нормаль к поверхности
![]() (см. рис.4.3).
(см. рис.4.3).
![]() , (4.9)
, (4.9)
 . (4.10)
. (4.10)
Пример 1.
Используя определение частной
производной, найти частные производные
функции
![]() .
.
Решение. 1. Находим
![]() .
.
Воспользуемся
формулой
 ,
тогда
,
тогда


2. По формулам (4.4)
 ,
,
 .
.
Ответ.
![]() ,
,
 .
.
Пример 2. Найти частные производные функций по каждой из независимых переменных.
а)
![]() .
.
Решение. 1.
Найдем
![]() ,
предполагая, что изменяется
,
предполагая, что изменяется
![]() ,
а
,
а
![]() остается
постоянной:
остается
постоянной:
 .
.
2. Найдем
![]() ,
предполагая, что изменяется
,
предполагая, что изменяется
![]() ,
а
,
а
![]() остается постоянной:
остается постоянной:
 .
.
Ответ.
![]() ,
,
 .
.
б)
![]() .
.
Решение.
 ,
,
 .
.
Ответ.
 ,
,
 .
.
в)
![]() .
.
Решение. 1.
Найдем
![]() предполагая что изменяется
предполагая что изменяется
![]() ,
а
,
а
![]() остается постоянной, тогда необходимо
воспользоваться формулой 2 таблицы
производных:
остается постоянной, тогда необходимо
воспользоваться формулой 2 таблицы
производных:

2. Найдем
![]() предполагая что изменяется
предполагая что изменяется
![]() ,
а
,
а
![]() остается постоянной, тогда необходимо
воспользоваться формулой 5 таблицы
производных:
остается постоянной, тогда необходимо
воспользоваться формулой 5 таблицы
производных:

Ответ.
 ,
,
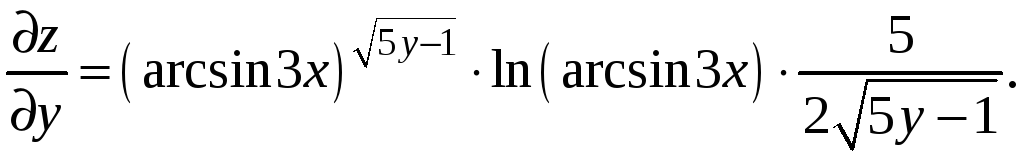
г)
![]() .
.
Решение. Функция
![]() ‑ функция четырех независимых
переменных. Эта функция будет иметь
четыре частных производных.
‑ функция четырех независимых
переменных. Эта функция будет иметь
четыре частных производных.
При постоянных
![]() и
и
![]() получаем:
получаем:
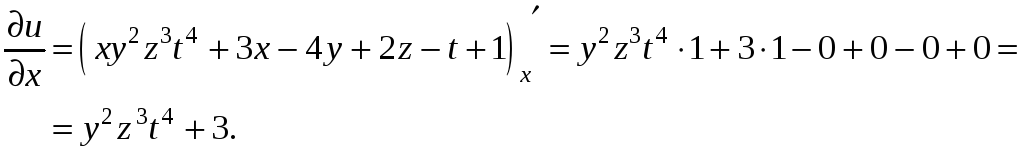
При постоянных
![]() и
и
![]() получаем:
получаем:

При постоянных
![]() и
и
![]() получаем:
получаем:

При постоянных
![]() и
и
![]() получаем:
получаем:

Ответ.
![]() ,
,
 ,
,
![]() ,
,
![]() .
.
Пример 3. Найти частные производные сложных функций.
а)
![]() ,
где
,
где
![]() ,
,
![]() .
.
Решение. Данная сложная функция двух переменных удовлетворяет условиям теоремы 2, поэтому её частные производные могут быть найдены по формулам (4.5).
Найдем
![]() и
и
![]() :
: ![]() ,
,
 .
.
Найдем
![]() и
и
![]() :
: ![]() ,
,
 .
.
Найдем
![]() и
и
![]() :
: ![]() ,
,
 .
.
По формулам (4.5)
получаем:
 ,
,
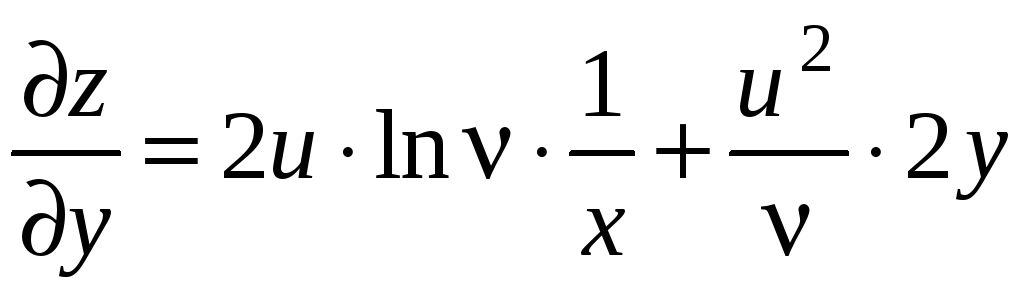 .
.
Ответ.
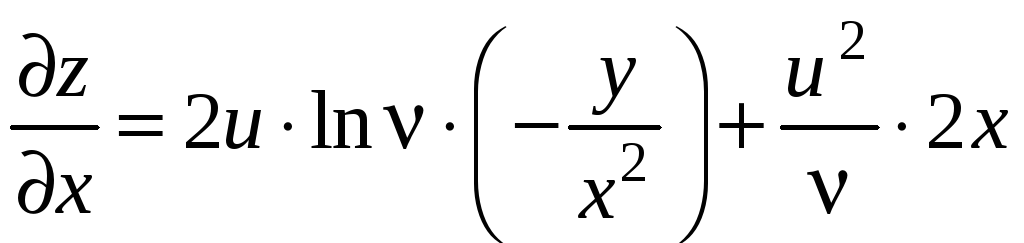 ,
,
 .
.
б)
![]() ,
где
,
где
![]() .
.
Решение. Данная
сложная функция двух переменных
удовлетворяет условиям теоремы 3,
поэтому её производную
![]() можно найти по формуле (4.6).
можно найти по формуле (4.6).
Найдем
![]() и
и
![]() :
: ![]() ,
,
 .
.
Найдем
![]() и
и
![]() :
: ![]() ,
,
 .
.
Тогда по формуле
(4.6):
 .
.
Ответ.
 .
.
в)
 ,
где
,
где
![]() .
.
Решение. Данная
сложная функция двух переменных
удовлетворяет условиям следствия
теоремы 3, поэтому её производную
![]() можно найти по формуле (4.7).
можно найти по формуле (4.7).
Найдем
![]() и
и
![]() :
:
 ,
,
 .
.
Найдем
![]() :
:
![]() .
По формуле (4.7) получаем:
.
По формуле (4.7) получаем:
 ,
,
тогда
 ,
,
или  .
.
Ответ.
 .
.
Пример 4.
Найти уравнение касательной плоскости
и нормали к поверхности
![]() в точке
в точке
 .
.
Решение. 1)
Найдем
![]() и
и
![]() :
:
 ,
,
 .
.
2) По формуле (4.9) касательная плоскость имеет уравнение:
 ;
;
![]() или
или
![]() .
.
По формуле (4.10) каноническое уравнение нормали к данной поверхности имеет вид:
 или
или  .
.
Ответ.
![]() ,
,
 .
.
