2. Производная функции, заданной параметрически.

Пусть дана параметрически заданная функция одной переменной

, где ‑ параметр и .

Производную такой функции находят по формуле:

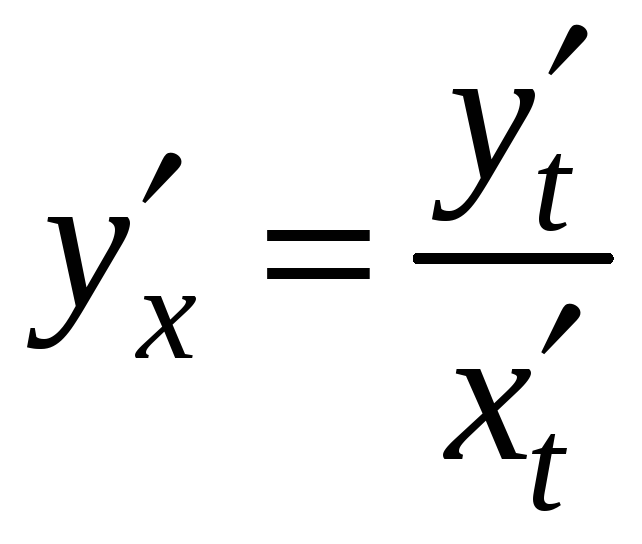(5.5)

Пример 3. Найти , если

Решение. , .

Ответ. .

2. Логарифмическое дифференцирование.

Операция, состоящая в последовательном применении к функции сначала логарифмирования, а затем дифференцирования, называется логарифмическим дифференцированием.

Логарифмическое дифференцирование обычно применяется при отыскании производной от степенно‑показательной функции , где , ( ‑ для функции двух независимых переменных) и от произведения функций, т.е. в тех случаях, когда обычными методами производную нельзя найти или вычисление производной очень громоздко.

Пример 4. Найти производные или частные производные по каждой из независимых переменных от заданных функций.

а) .

Решение. 1) Прологарифмируем функцию: . По свойству логарифма , получаем ‑ неявно заданная функция одной переменной.

2) Найдем производную этой функции, используя способ I:

.

Выразим :

или .

Ответ. .

б) .

Решение. 1) Прологарифмируем функцию: .

или ‑ неявно заданная функция двух переменных.

2) Найдем частные производные этой функции, используя способ I:

,

,

или ;

,

,

или .

Ответ. ,

.

в) .

Решение.

1) Прологарифмируем функцию: , по свойству логарифма: , т.е. получили неявно заданную функцию одной переменной.

2) Найдем частные производные этой функции, используя способ I:

,

,

или

.

Ответ. .

Задачи для самостоятельного решения

Найти производную или частные производные по каждой из независимых переменных функций, заданных неявно, двумя способами.

5.1.

5.2.

Найти производную или частные производные по каждой из независимых переменных от функций, заданных неявно любым способом.

5.3.

5.4.

5.5.

5.6.

5.7.

5.8.

5.9.

5.10.

5.11.

5.12.

Найти производные от по .

5.13.

5.14.

5.15.

5.16.

5.17.

5.18.

Найти производные по каждой из независимых переменных.

5.19.

5.20.

5.21.

5.22.

5.23.

5.24.

5.25.

6. Практическое занятие по теме: Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков

Если функция дифференцируема в точке , то ее полное приращение можно представить в форме двух слагаемых ‑ главной части приращения и бесконечно малой величины:

.

Определение. Дифференциалом дифференцируемой в точке функции называется главная линейная относительно приращений аргументов часть приращения этой функции в точке :

,

где .

Для функции имеем

. (6.1)

Для функции имеем

. (6.2)

Достаточным условием дифференцируемости функции в точке является наличие непрерывных частных производных в этой точке. Для функции достаточным условием является существование производной в данной точке.

С точки зрения геометрии дифференциал функции равен приращению ординаты касательной к графику функции в данной точке. Для функции дифференциал есть приращение аппликаты касательной плоскости к поверхности в данной точке.