§ 9. Формула Тейлора

1. Пусть функция определена в некоторой окрестности точки а и имеет там конечные производные до порядка включительно. Значит, сама функция и ее производные до порядка () включительно непрерывны в окрестности . Утверждаем, что при этих условиях для любого х из имеет место равенство

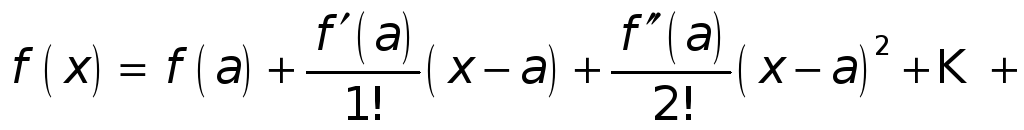
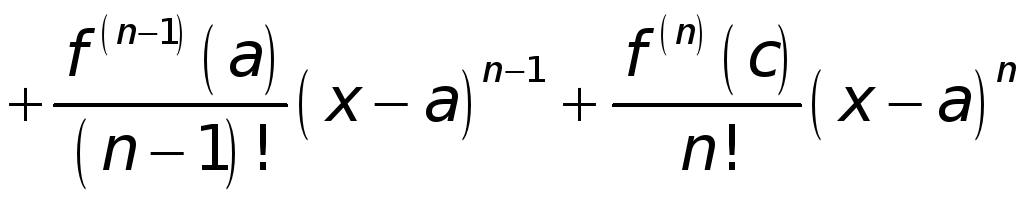. (1)

Здесь точка с есть некоторая точка, лежащая между точкой а и точкой х.

► Возьмем в окрестности любые две точки и () и закрепим их. Введем в рассмотрение число

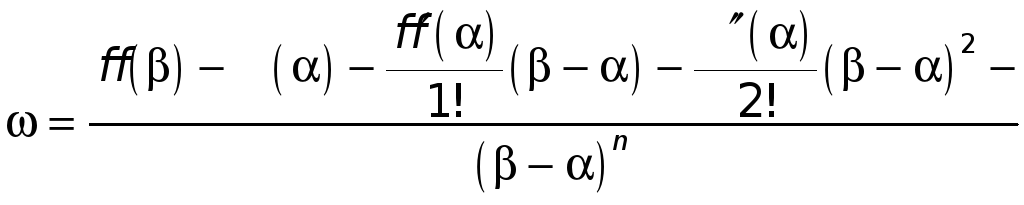
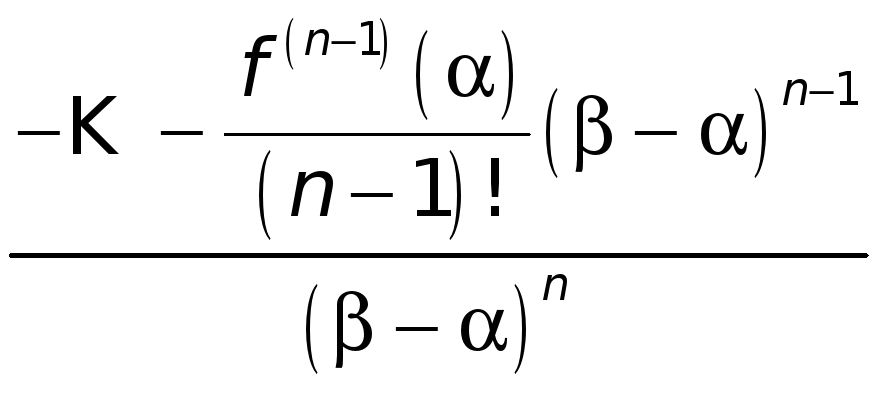, (2)

откуда

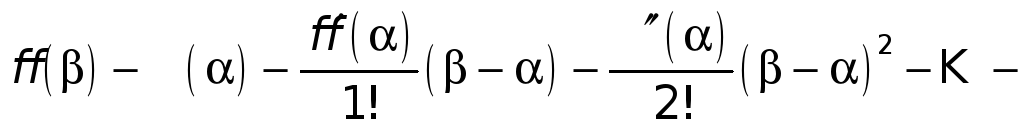
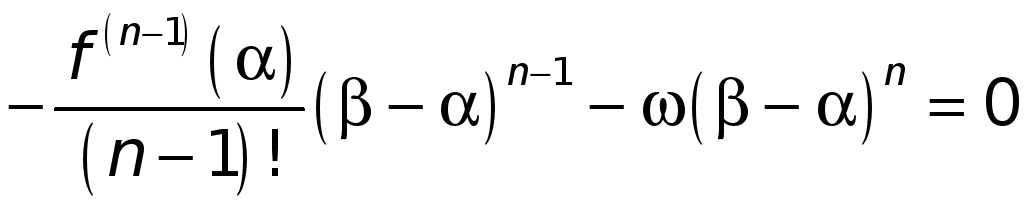. (3)

Введем в рассмотрение вспомогательную функцию

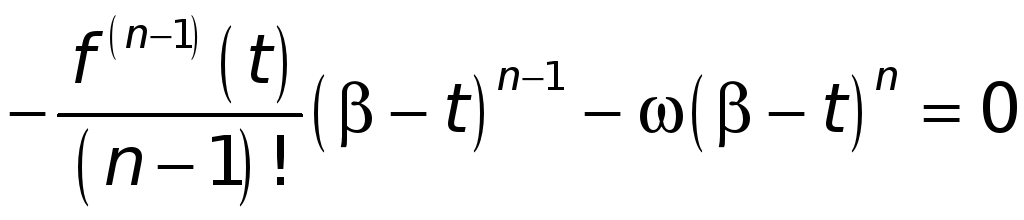. (4)

Отметим, что:

1) определена и непрерывна на промежутке , ибо на этом промежутке определены и непрерывны , , , …, .

2) имеет конечную производную в промежутке , ибо

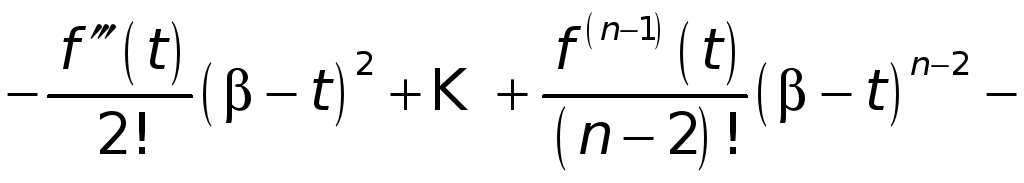
, (5)

а , , …, , существуют конечные в по условию. Из (5) после сокращения находим

.

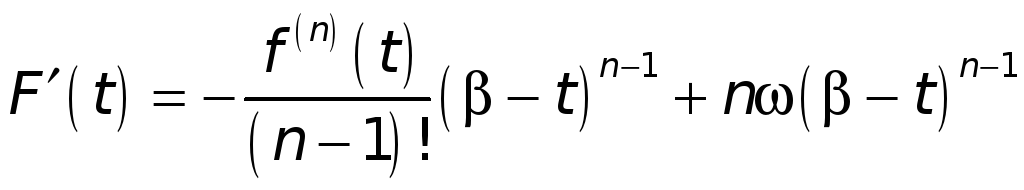3) (в силу (3); — это очевидно из (4)).

Видим, что функция удовлетворяет всем трем условиям теоремы Ролля. По этой теореме между точками и обязательно найдется хотя бы одна точка с такая, что будет: , т. е.

,

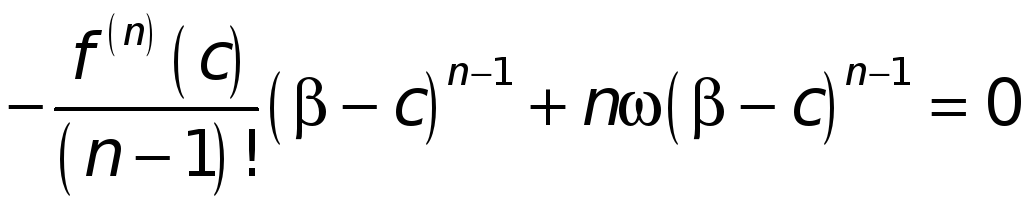откуда .

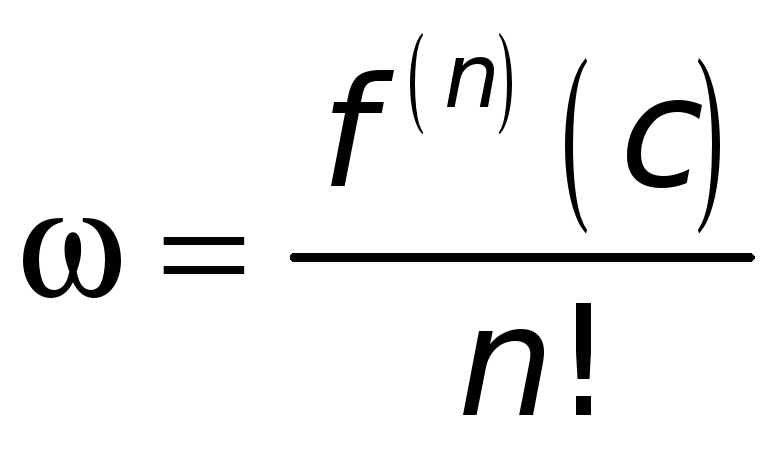Подставив полученное выражение для в соотношение (3), будем иметь

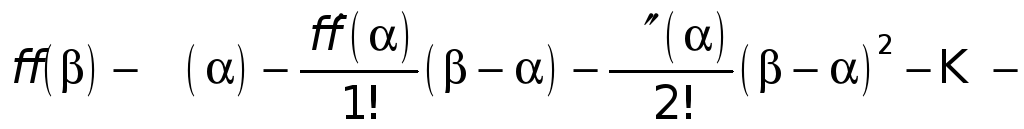
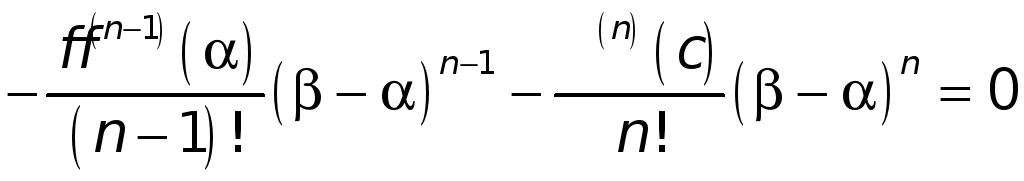. (6)

откуда

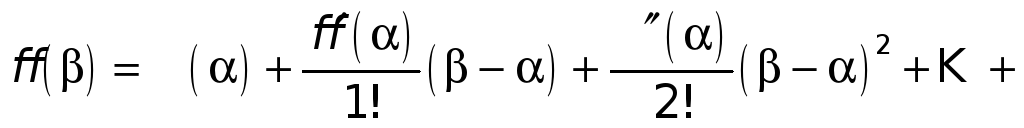
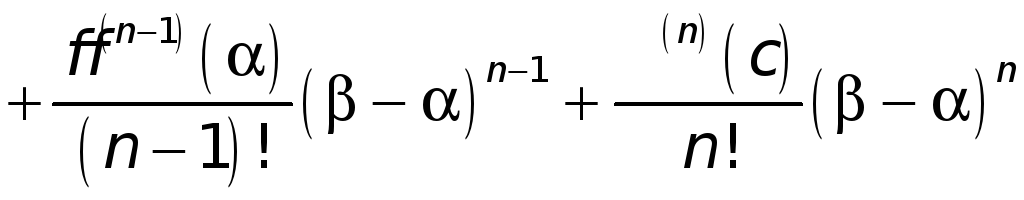. (7)

У нас точки и — любые из . Положим в (7) , . Получим

,

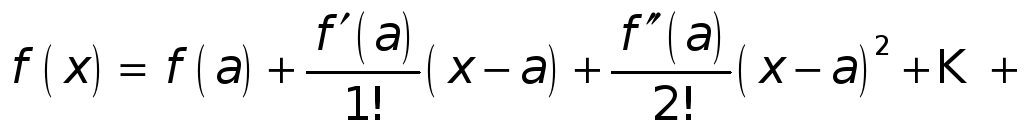
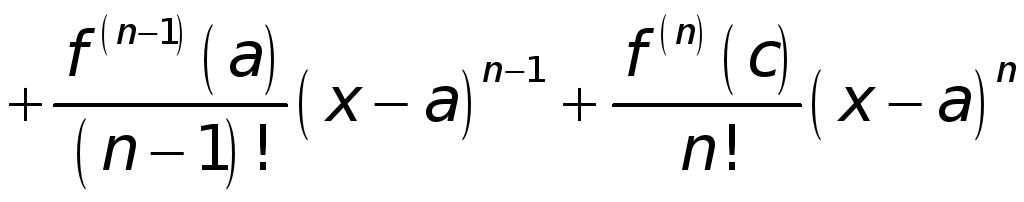где точка с есть некоторая точка, лежащая между точками а и х. ◄

Формула (1) называется формулой Тейлора с остаточным членом в форме Лагранжа. (Остаточным членом называют ).

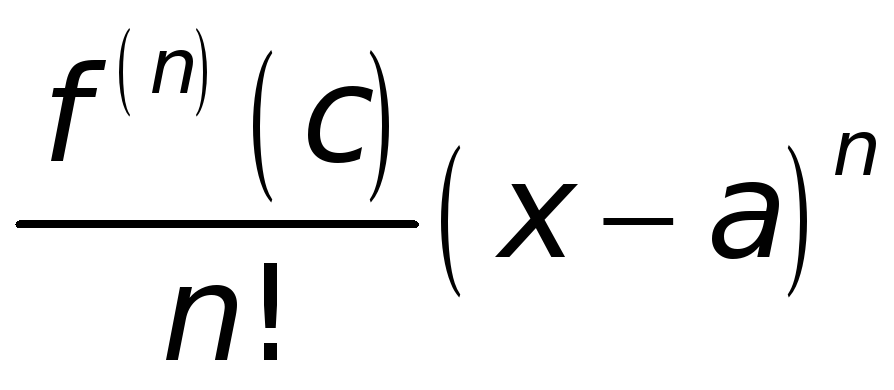Заметим, что остаточный член в форме Лагранжа напоминает очередной член формулы Тейлора; только -я производная вычислена не в точке а, а в некоторой промежуточной точке с, лежащей между точками а и х.

Замечание. При выводе формулы Тейлора с остаточным членом в форме Лагранжа мы предполагали, что функция имеет в промежутке конечные производные до порядка включительно, из этого следовало, что сама функция и ее последовательные производные до порядка () включительно непрерывны в промежутке . Что касается , то ее непрерывность не предполагалась. Потребуем теперь дополнительно, чтобы была непрерывной хотя бы в точке а.

Так как точка с лежит между точками а и х, то , если . А тогда, в силу непрерывности в точке а, будем иметь: . Следовательно, можем написать , где при . А тогда

,

где при . Заметим, что представляет собой бесконечно малую величину более высокого порядка по сравнению с бесконечно малой величиной , ибо

.

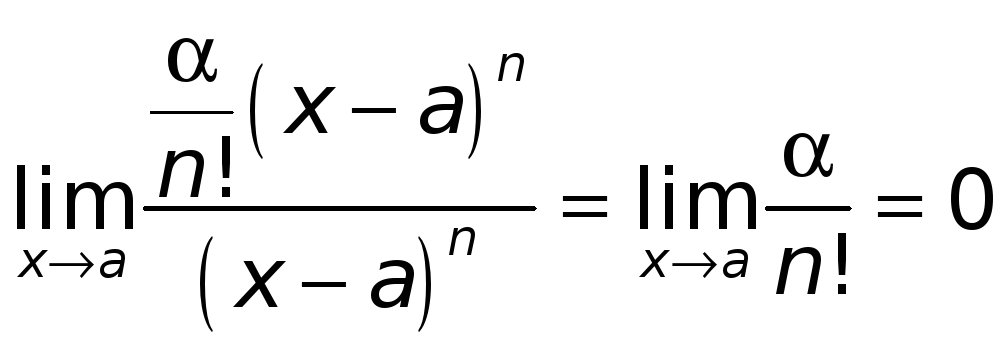Поэтому можно написать при .

Принимая во внимание все сказанное выше, будем иметь

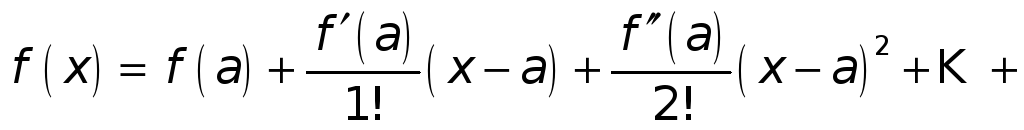
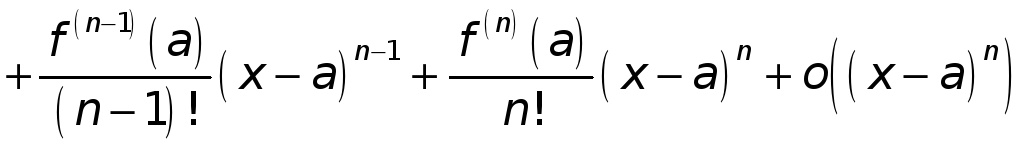. (8)

Формула (8) называется формулой Тейлора с остаточным членом в форме Пеано. Формулу (8) называют также локальной формулой Тейлора. Эта формула показывает, что, заменив в окрестности точки а ее многочленом Тейлора

,

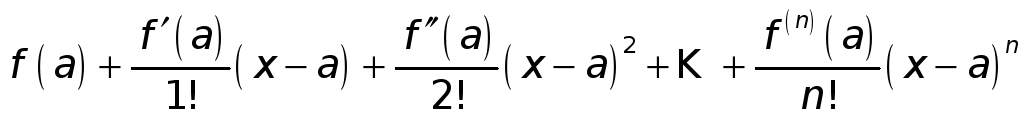мы совершим ошибку, которая при представляет собой бесконечно малую более высокого порядка, чем .

Замечание 1. В частном случае, когда , формулы Тейлора (1) и (8) называют формулами Маклорена с остаточными членами в форме Лагранжа и Пеано соответственно. Это будут следующие формулы:

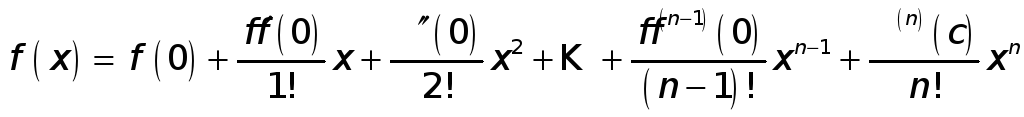, (1а)

где ;

.

(8а)

Замечание 2. Формула Тейлора имеет важные применения во многих вопросах математического анализа и его приложений. В частности, во многих случаях она позволяет функцию сложной природы с большой степенью точности заменить полиномом, т. е. функцией более простой; дает простой способ приближенного вычисления значений функции.

Замечание 3. Пусть , . Форула Тейлора с остаточным членом в форме Лагранжа запишется так:

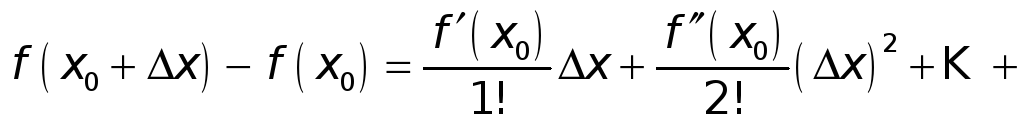
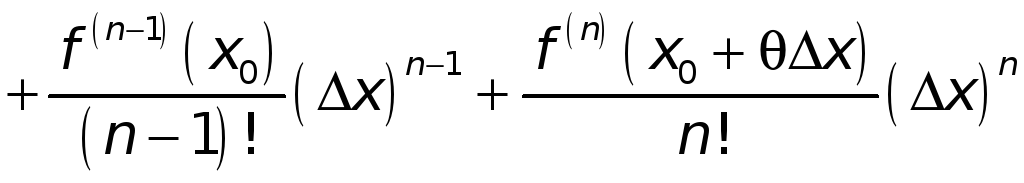
или

.
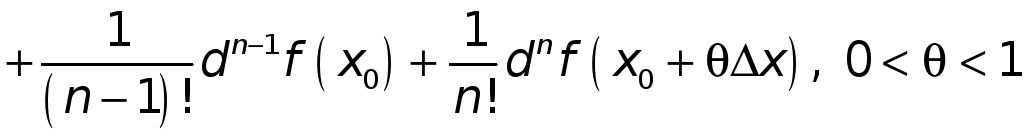