2. Примеры разложения по формуле Тейлора.
1.
.
Напишем для этой функции формулу
Маклорена. Имеем
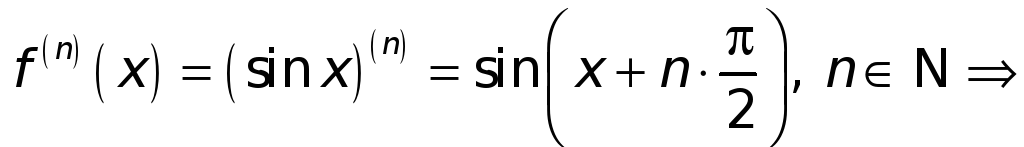
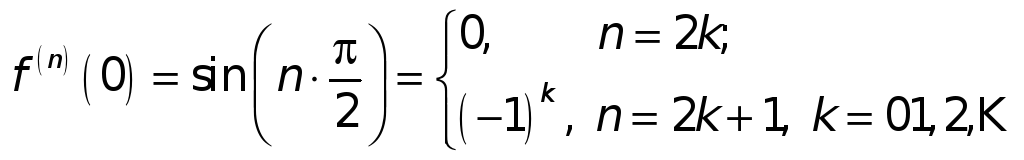
Согласно формуле (1а) находим
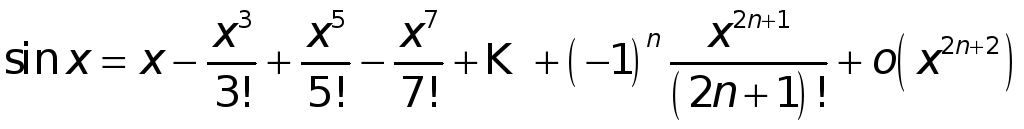при
.
Мы записали здесь
остаточный член в виде
,
а не в виде
,
так как следующий за выписанным слагаемым
член формулы Маклорена равен нулю.
2.
.
Напишем для этой функции формулу
Маклорена. Имеем
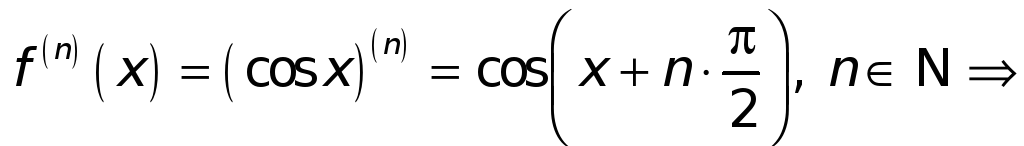
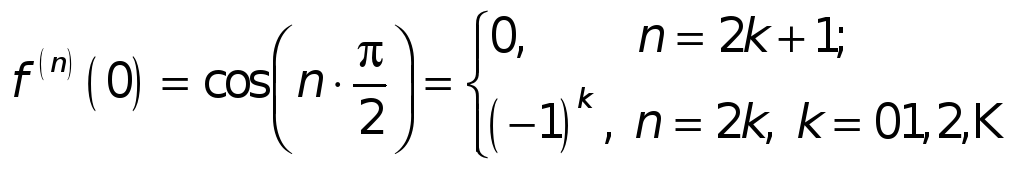
Согласно формуле (1а) находим
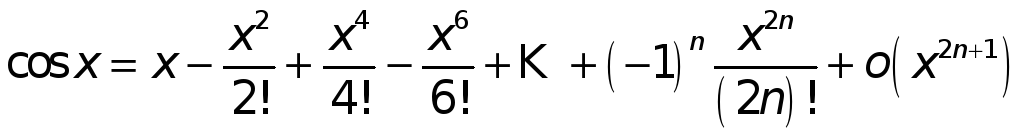при
.
3.
.
Получим для этой функции формулу
Маклорена. Имеем
Согласно формуле (1а) находим
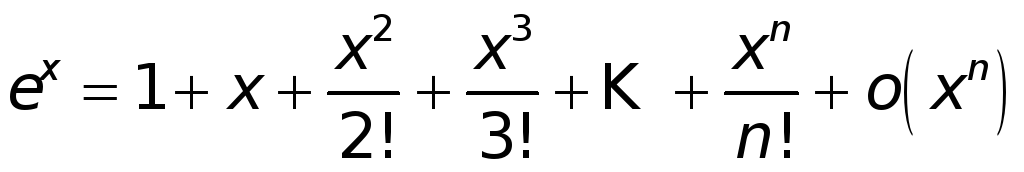при
(9)
.
Заменяя в формуле
(9)
на
,
получим
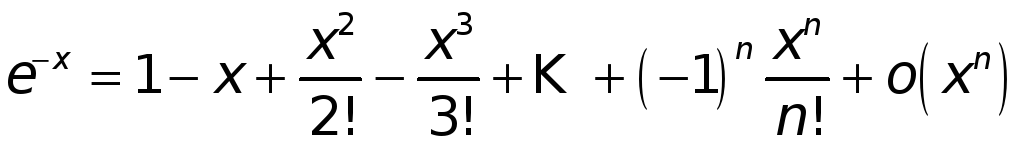при
(10)
.
4.
и
.
Вычитая из формулы (9) соответствующие
части формулы (10), получаем
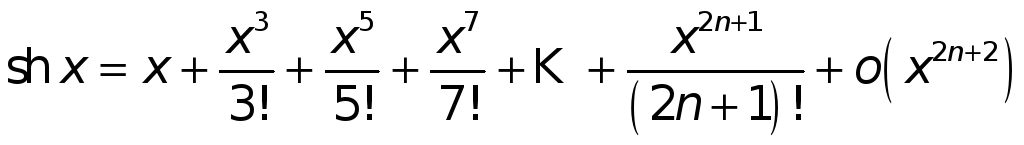при
.
Складывая соответствующие части формул (9) и (10), находим
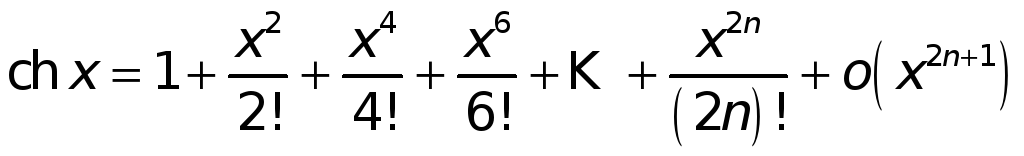при
.
5.
(
— любое вещественное число, не равное
нулю). Получим для этой функции формулу
Маклорена. Имеем
;
;
;
……………………………………
;
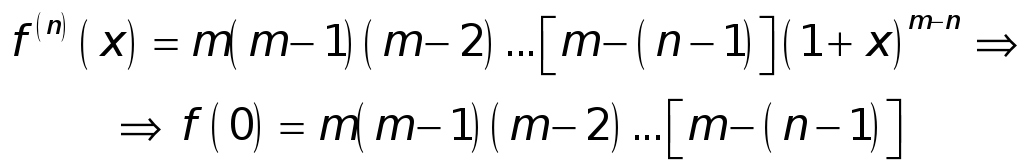Согласно формуле (8а) находим
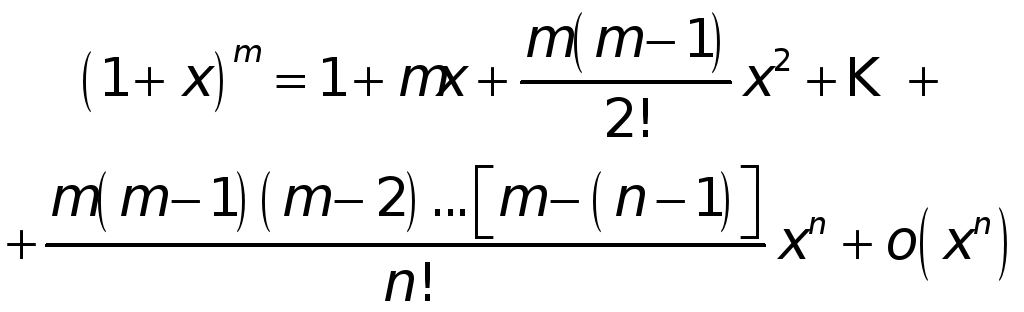
при
.
6.
.
Получим для этой функции формулу
Маклорена. Имеем
;
;
;
;
……………………………………
.
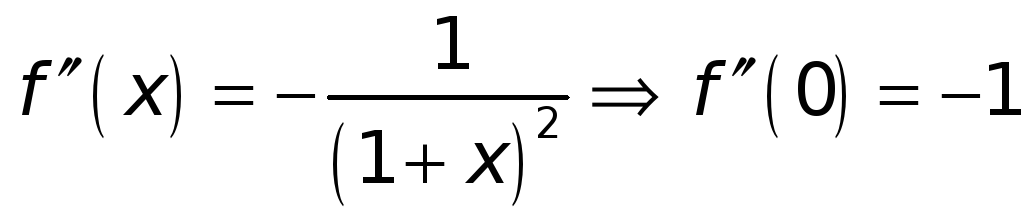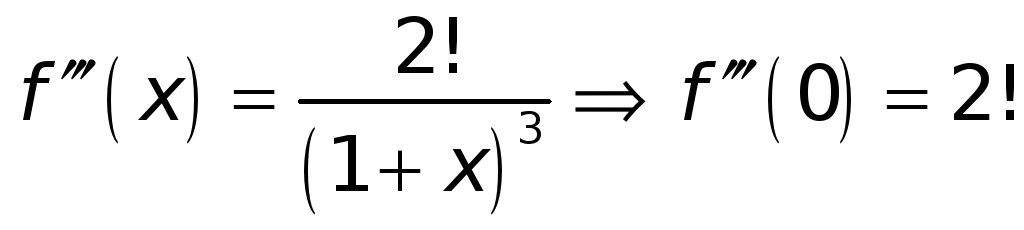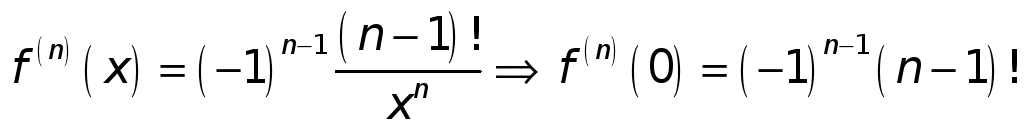Согласно формуле (8а) находим
при
.
§ 10. Раскрытие неопределенностей по правилу Лопиталя
Под раскрытием неопределенностей понимают вычисление пределов функций в некоторых особых, но часто встречающихся случаях.
Пусть, например, речь идет о вычислении
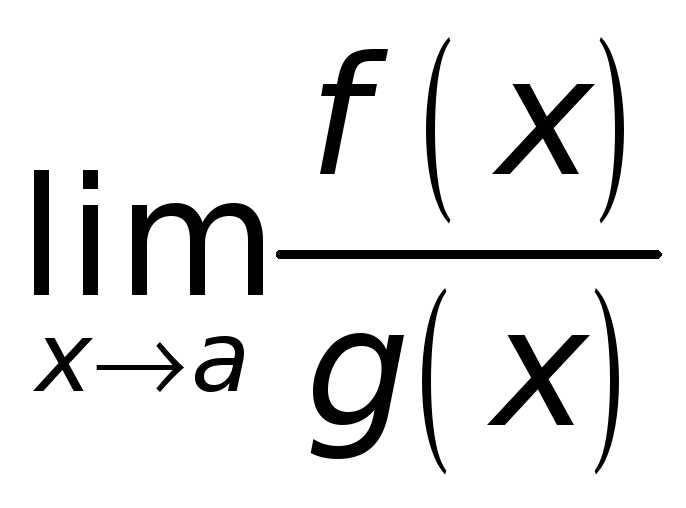(1)
в случаях, когда
и
при
одновременно стремятся либо к нулю,
либо к бесконечности. Непосредственное
применение правила вычисления предела
дроби здесь невозможно. Формальное же
применение этого правила приводит к
символу
или, соответственно
.
В связи с этим
говорят, чтоотношение
при
в этих случаях представляет собой
неопределенность вида
или
.
В этом параграфе
мы дадим некоторые общие правила для
раскрытия неопределенностей вида
или
,
носящих общее название правил Лопиталя.
1. Неопределенность вида .
Теорема 1.
Пусть функции
и
:
1) определены в
промежутке
(
— конечное число,
);
2) имеют конечные
производные
и
в
,
причем
для
;
3) 
;
.
Тогда, если существует конечный или бесконечный (определенного знака) предел
,
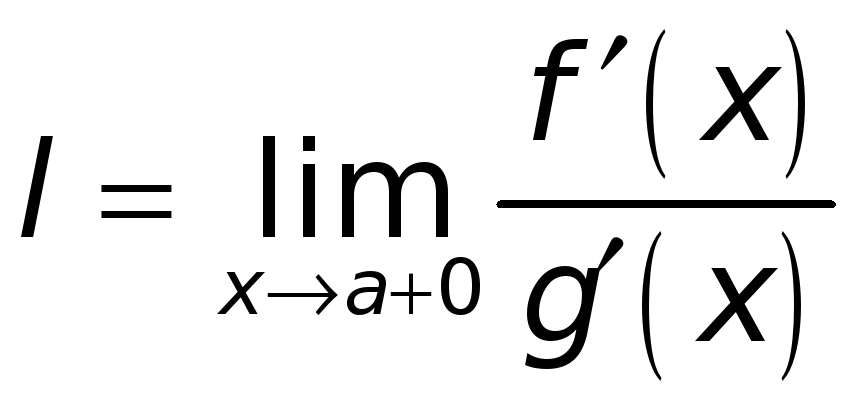то к тому же пределу
/
при
стремится и отношение
,
(т.е.
).
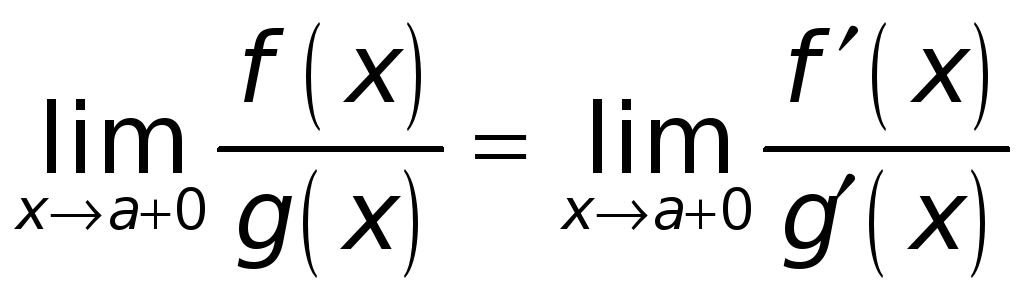► Из условия 1)
теоремы следует, что функции
и
не определены в точке а.
Доопределим эти функции в точке а,
положив
,
.
Возьмем любое х
из промежутка
(а
< х
< b).
Ясно, что теперь на промежутке [а, х]
функции
и
удовлетворяют условиям теоремы Коши.
Поэтому для каждого х
из промежутка
между точками а
и х
существует точка с
такая, что имеет место равенство
,
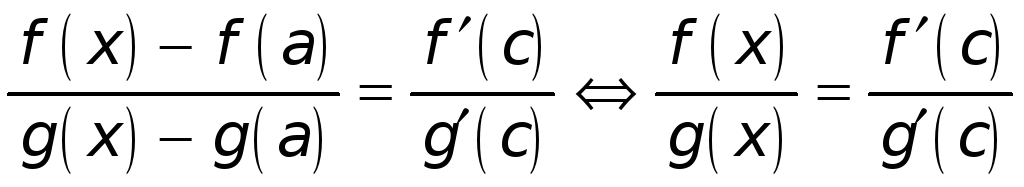ибо у нас
,
.
Так как точка с
лежит между точками а
и х,
то
,
если
.
В соотношении
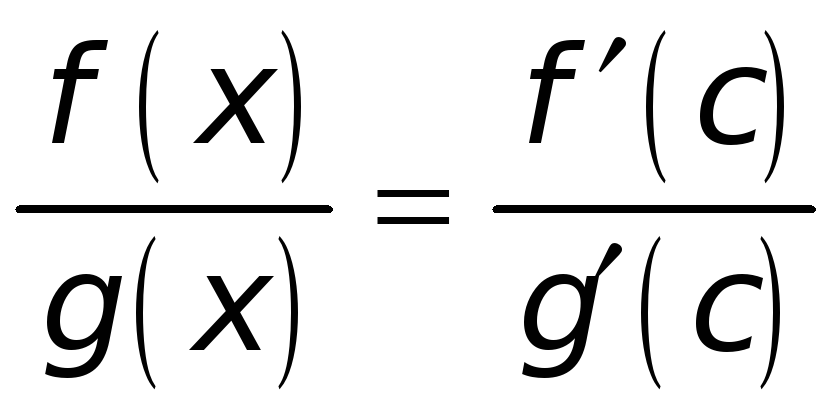перейдем к пределу при
.
Получим
.
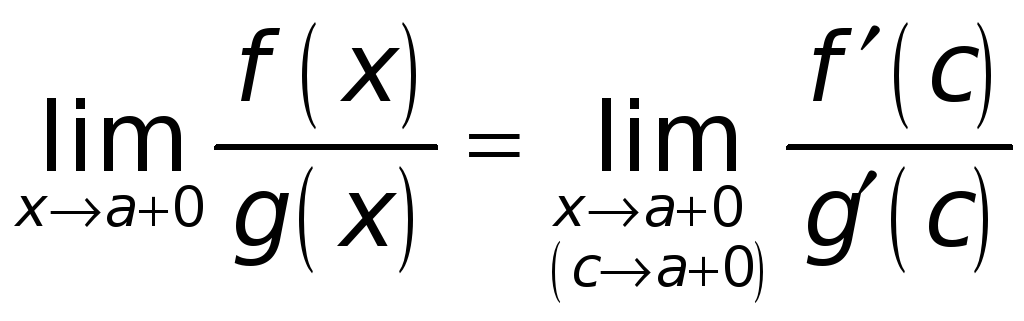По условию
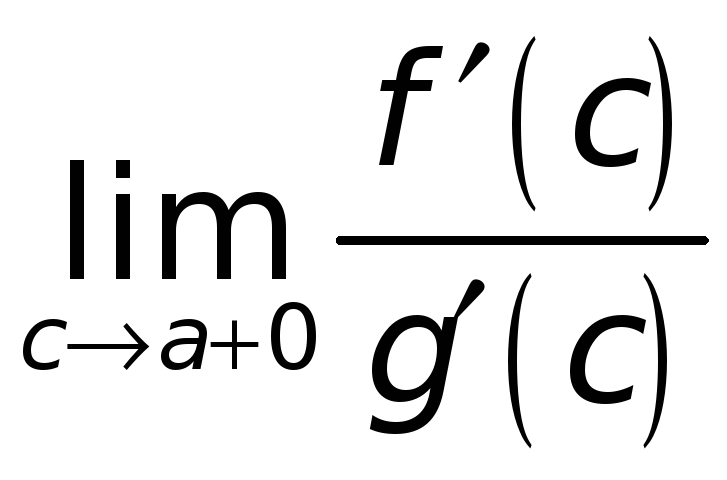существует и равен
(
— конечное число или бесконечность
определенного знака). Но тогда и
.
◄
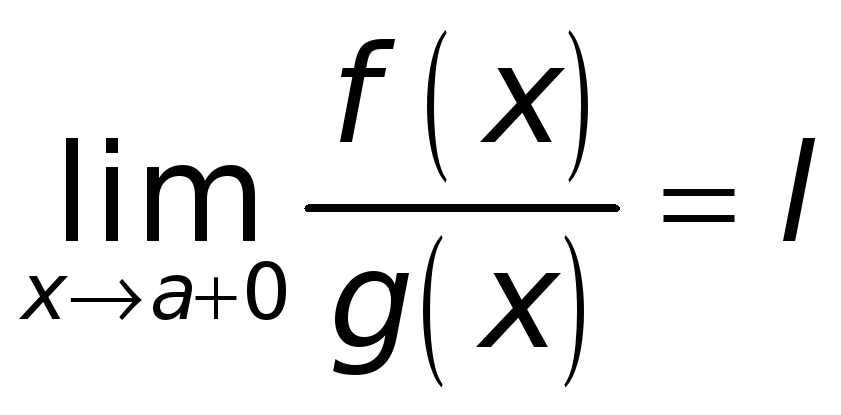Замечание.
В теореме 1 речь шла о правостороннем
пределе отношения
в точке а.
Отметим, что совершенно аналогичные
утверждения остаются справедливыми в
случаях, когда речь идет о левостороннем
или двустороннем пределе отношения
в точке а.
Пример.
Найти
.
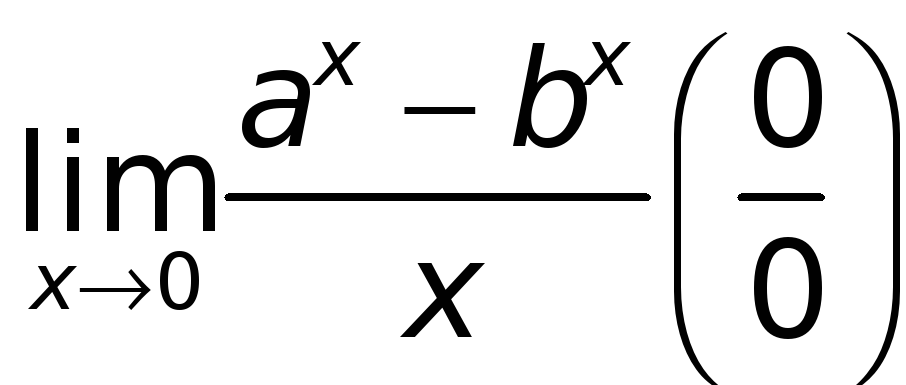► Здесь
,
.
Ищем предел отношения производных
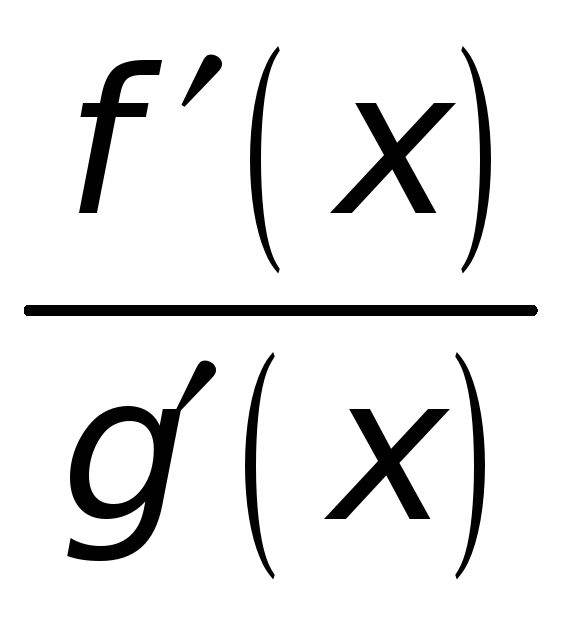при
.
Имеем
.
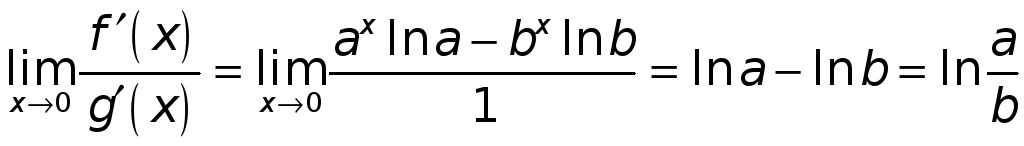Значит, и
.
◄
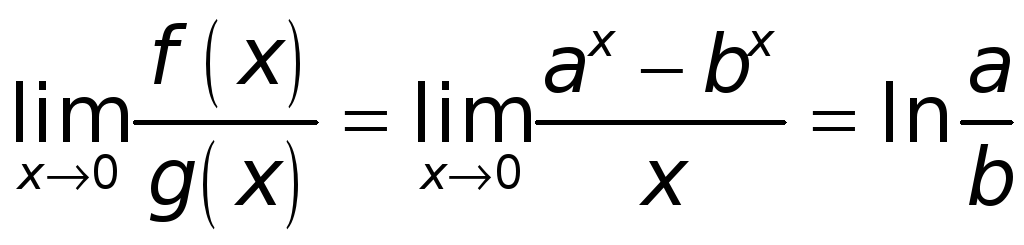Замечание. Может случиться, что отношение производных опять
приводит к
неопределенности вида
.
Но к отношению производных можно
снова применить установленное правило
(если, конечно, выполнены условия его
применимости), т. е. перейти к отношению
вторых производных. Если и здесь
получается неопределенность
,
то переходим к отношению третьих
производных и т. д. Если на каком-то шаге
мы получим предел, который сможем
вычислить, то найденное его значение и
будет искомым пределом отношения
функций.
Замечание. Если не существует предел отношения производных, то это вовсе не означает, что не существует и предел отношения самих функций.
Например, пусть
.
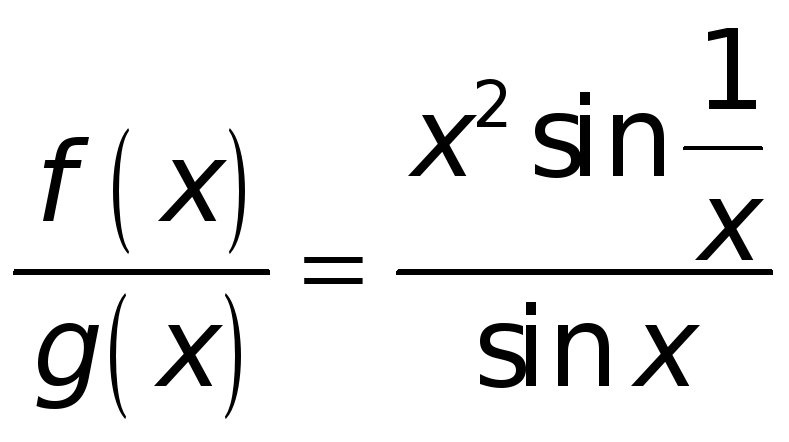Это отношение представляет собой при
неопределенность вида
.
Имеем
.
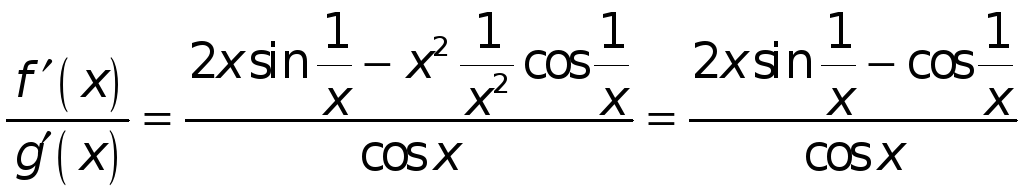Ясно, что
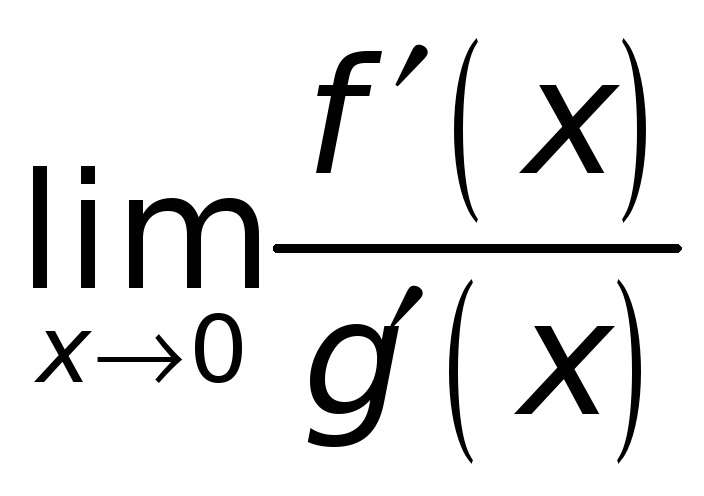не существует, так как не существует
.
Однако
,
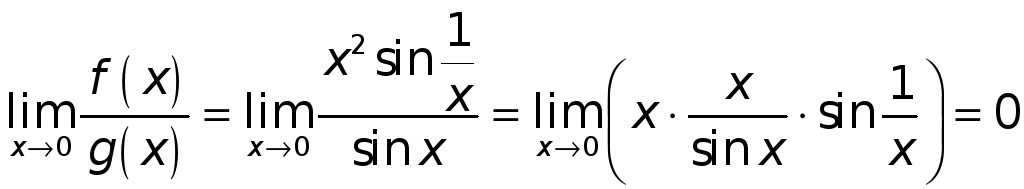ибо
,
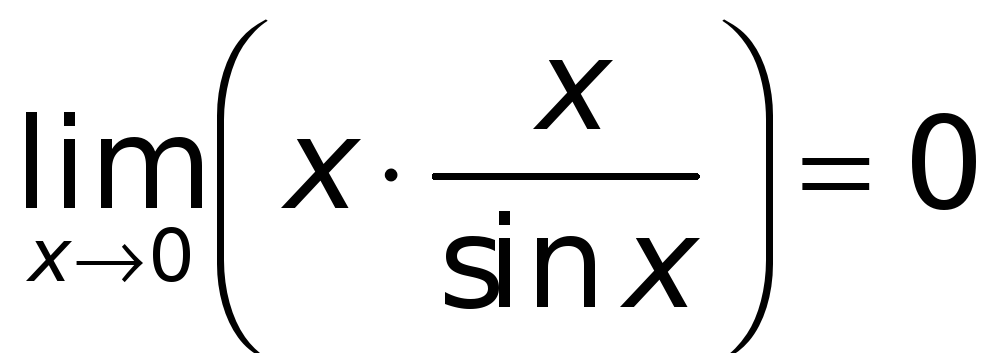а функция
— ограниченная.
Замечание.
Теорема 1 доказана для случая, когда
— конечное число. Отметим. Что утверждение
теоремы справедливо и для случая, когда
— несобственное число
.