
- •Глава 4 Производная и дифференциал § 1. Производная. Механический и геометрический смысл производной
- •4. Односторонние производные.
- •§2. Понятие дифференцируемости функции
- •§ 3. Формулы и правила вычисления производных
- •7. Простейшие правила вычисления производных.
- •12. Формула для приращения функции.
- •13. Правило дифференцирования сложной функции.
- •14. Правила дифференцирования обратных функций.
- •§ 4. Дифференциал функции
- •2. Геометрический смысл дифференциала.
- •3. Сводка формул для дифференциалов.
- •4. Дифференциал сложной функции. Инвариантность формы дифференциала.
- •§ 5. Производные высших порядков
- •2. Формула Лейбница для производной n-го порядка от произведения двух функций.
- •3. Механическое истолкование второй производной.
- •§ 6. Дифференциалы высших порядков
- •§ 7. Дифференцирование функции, заданной параметрически
- •§ 8. Основные теоремы дифференциального исчисления
- •§ 9. Формула Тейлора
- •2. Примеры разложения по формуле Тейлора.
- •§ 10. Раскрытие неопределенностей по правилу Лопиталя
- •1. Неопределенность вида .
- •2. Неопределенность вида .
- •§ 11. Признаки постоянства, возрастания и убывания функций
- •§ 12. Теория экстремальных значений функции
- •2. Исследование стационарных критических точек функции с помощью второй производной.
- •§ 13. Характер выпуклости кривой. Точки перегиба
- •§ 14. Асимптоты кривой
- •§ 15. Построение графика функции по характерным точкам
§ 7. Дифференцирование функции, заданной параметрически
Бывают случаи,
когда зависимость переменной
![]() от переменной
от переменной
![]() не задана непосредственно, а вместо
этого задана зависимость обеих переменных
не задана непосредственно, а вместо
этого задана зависимость обеих переменных
![]() и
и
![]() от некоторой третьей, вспомогательной,
переменной t
(называемой параметром):
от некоторой третьей, вспомогательной,
переменной t
(называемой параметром):
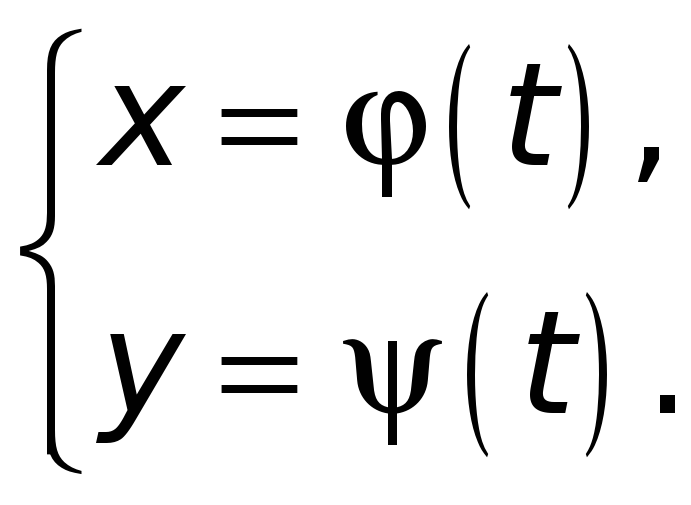 (1)
(1)
Считаем, что функции
![]() ,
,
![]() определены на одном и том же промежутке
определены на одном и том же промежутке
![]() .
.
Пусть точка
![]() и пусть в окрестности
и пусть в окрестности
![]() точки
точки
![]() функции
функции
![]() и
и
![]() имеют нужное количество конечных
производных по переменной
имеют нужное количество конечных
производных по переменной
![]() .
Будем предполагать, что
.
Будем предполагать, что
![]() в
в
![]() и что функция
и что функция
![]() строго монотонная в
строго монотонная в
![]() .
Но тогда, как мы знаем, у функции
.
Но тогда, как мы знаем, у функции
![]() существует обратная
функция
существует обратная
функция
![]() ,
определенная в окрестности
,
определенная в окрестности
![]() точки
точки
![]() (
(![]() ;
;![]() — образ
— образ
![]() при отображении
при отображении
![]() ).
).
Отметим, что функция
![]() в
в
![]() будет непрерывной, строго монотонной
и имеющей конечную производную
будет непрерывной, строго монотонной
и имеющей конечную производную
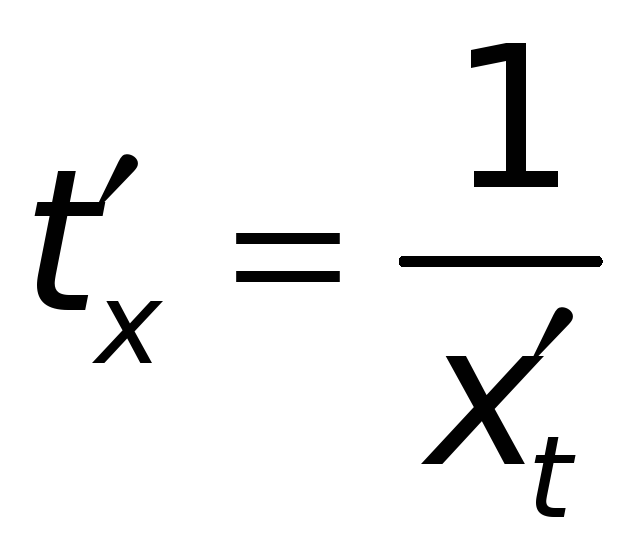 .
Подставив
.
Подставив
![]() в соотношение
в соотношение
![]() ,
получим
,
получим
![]() .
(2)
.
(2)
Видим, что
![]() можно рассматривать как функцию
независимой переменной х,
а переменную
можно рассматривать как функцию
независимой переменной х,
а переменную
![]() считать промежуточным аргументом. По
правилу дифференцирования сложной
функции имеем:
считать промежуточным аргументом. По
правилу дифференцирования сложной
функции имеем:
![]() .
Так как
.
Так как
 ,
то окончательно получаем
,
то окончательно получаем
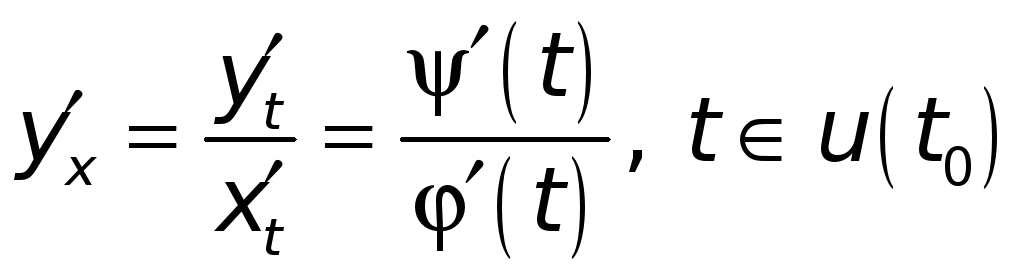 .
(3)
.
(3)
Пример. Пусть
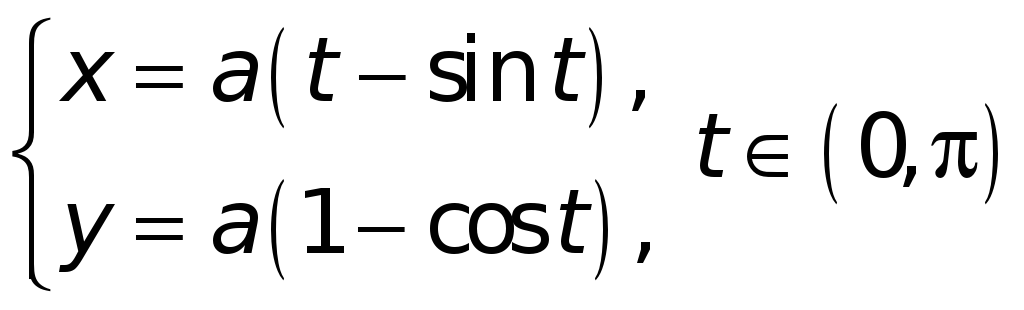 .
.
Имеем,
![]() .
.
Значит
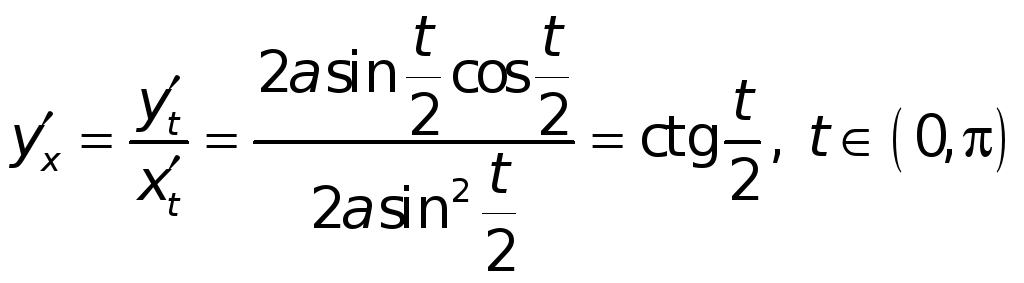
Чтобы найти
![]() ,
поступаем следующим образом. Замечаем,
что функция
,
поступаем следующим образом. Замечаем,
что функция
![]() параметрически задается уравнениями
параметрически задается уравнениями
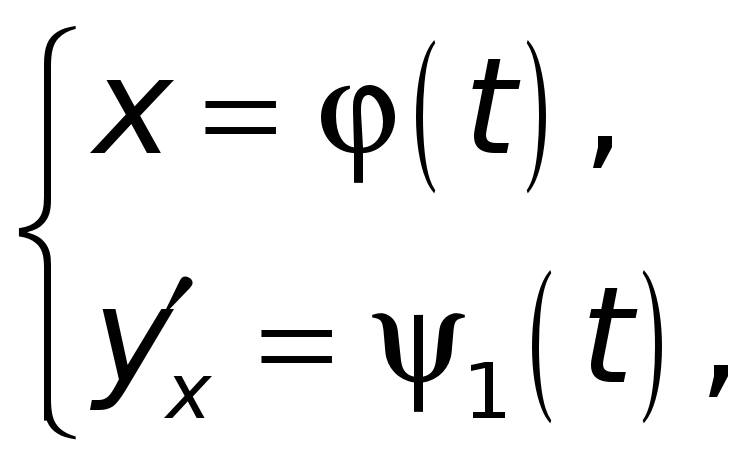 где
где
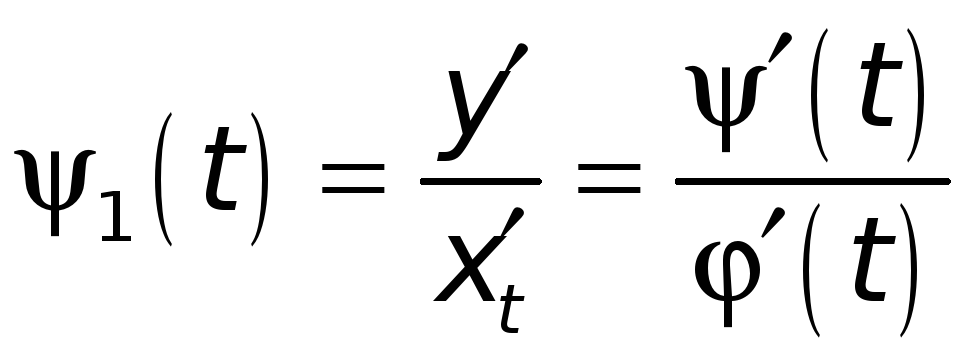 .
.
А тогда, по установленному выше (см. (3)), находим
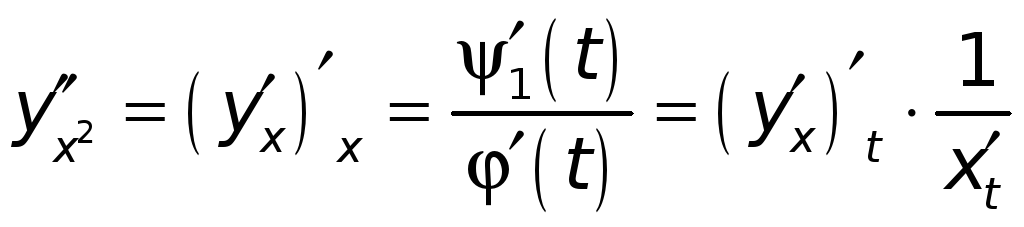 .
.
В нашем примере
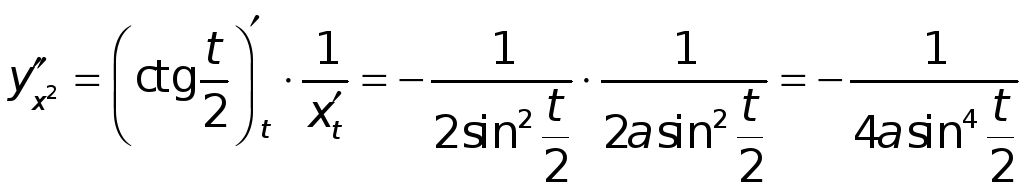 .
.
Аналогично, считая,
что функция
![]() задана параметрически уравнениями
задана параметрически уравнениями
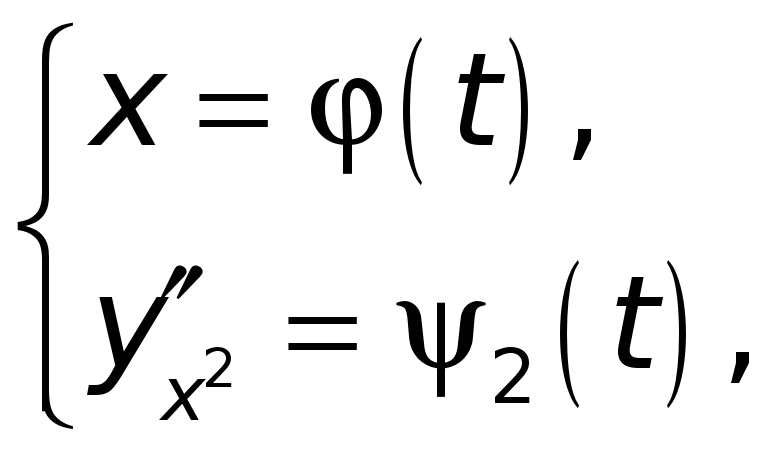 где
где
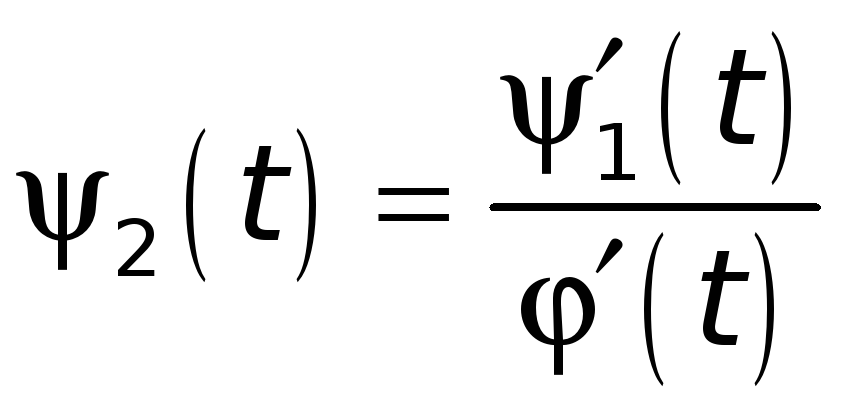 ,
,
находим
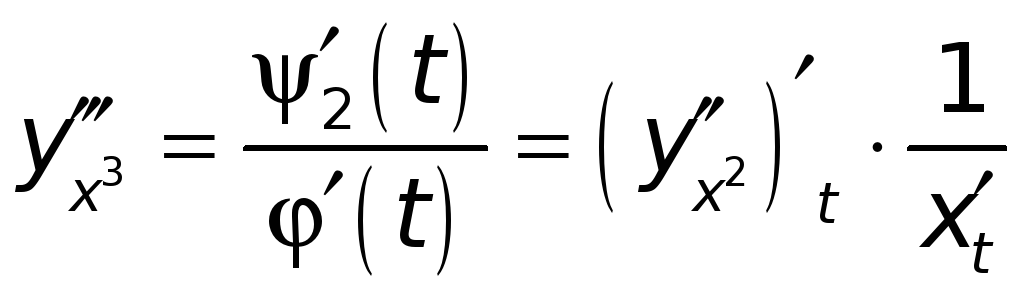
и т. д. И вообще для
любого
![]() получаем
получаем
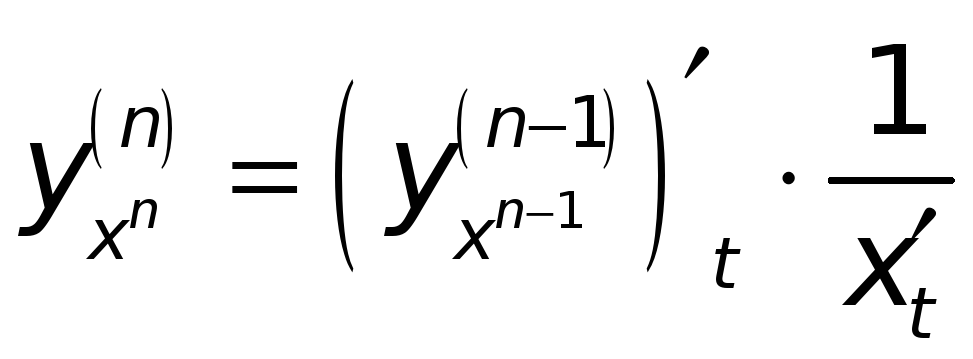 .
.
§ 8. Основные теоремы дифференциального исчисления
Пусть функция
![]() определена в некоторой окрестности
определена в некоторой окрестности
![]() точки
точки
![]() .
Если
.
Если
![]() в точке
в точке
![]() имеет конечную или бесконечную, но
определенного знака производную, то
будем говорить, что функция
имеет конечную или бесконечную, но
определенного знака производную, то
будем говорить, что функция
![]() в точке
в точке
![]() имеет
определенную производную.
имеет
определенную производную.
1. Теорема Ферма.
Пусть функция
![]() определена на замкнутом промежутке
определена на замкнутом промежутке
![]() и пусть в некоторой внутренней точке с
этого промежутка (т. е. в точке
и пусть в некоторой внутренней точке с
этого промежутка (т. е. в точке
![]() )
)
![]() принимает либо свое наибольшее, либо
свое наименьшее значение. Тогда, если
в этой точке с
функция
принимает либо свое наибольшее, либо
свое наименьшее значение. Тогда, если
в этой точке с
функция
![]() имеет определенную производную, то
обязательно
имеет определенную производную, то
обязательно
![]() .
.
► Пусть, для
определенности,
![]() в точке с
принимает свое наибольшее значение.
Тогда для всех
в точке с
принимает свое наибольшее значение.
Тогда для всех
![]() будет
будет
![]() .
.
1). Возьмем
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Имеем
.
Имеем
![]() .
Значит,
.
Значит,
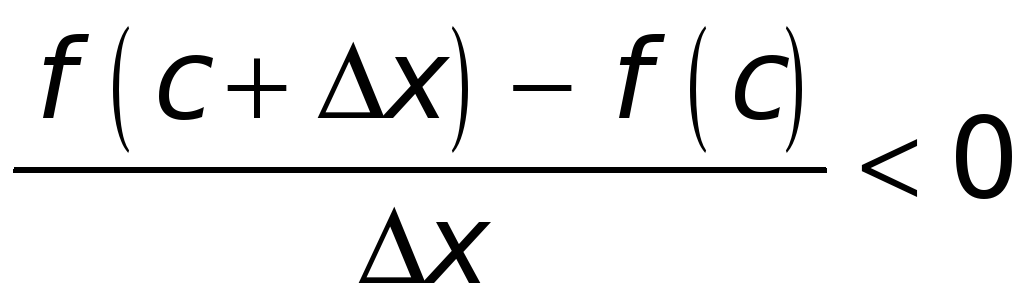 ,
,
и, следовательно,
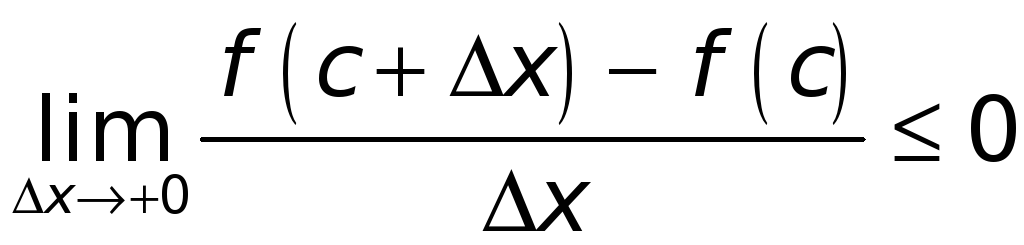 ,
т. е.
,
т. е.
![]() .
(*)
.
(*)
2). Возьмем теперь
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Имеем
.
Имеем
![]() .
Значит,
.
Значит,
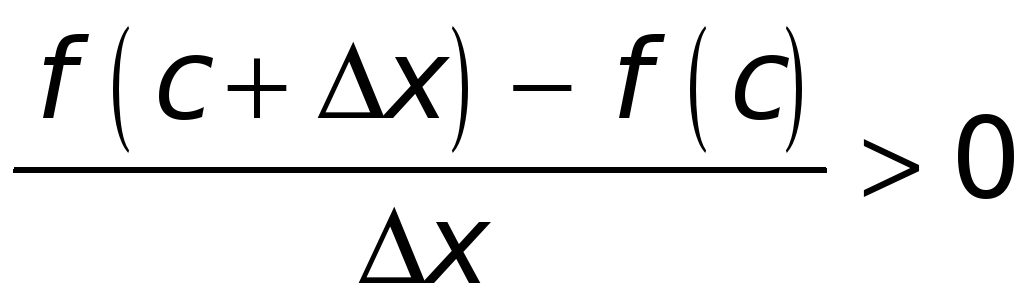 ,
,
и, следовательно,
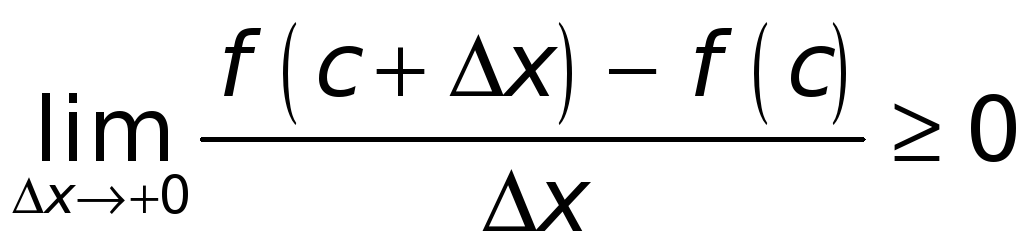 ,
т. е.
,
т. е.
![]() .
(**)
.
(**)
По условию функция
![]() в точке с
имеет определенную производную. Поэтому
правосторонняя и левосторонняя
производные функции
в точке с
имеет определенную производную. Поэтому
правосторонняя и левосторонняя
производные функции
![]() в точке с
должны совпадать. Но из (*) и (**) следует,
что осуществление соотношения
в точке с
должны совпадать. Но из (*) и (**) следует,
что осуществление соотношения
![]() возможно лишь тогда, когда
возможно лишь тогда, когда
![]() и
и
![]() ,
т. е. когда
,
т. е. когда
![]() .
◄
.
◄
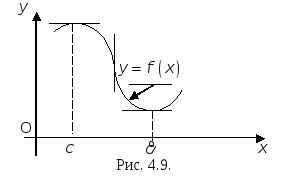
Геометрическая
интерпретация теоремы Ферма состоит в
том, что если в точке
![]() функция
функция
![]() принимает наибольшее или наименьшее
значение, то касательная к графику
функции
принимает наибольшее или наименьшее
значение, то касательная к графику
функции
![]() в точке
в точке
![]() параллельна оси Ох
(см. рис. 4.9).
параллельна оси Ох
(см. рис. 4.9).
Замечание.
Доказанная теорема неприменима, если
функция
![]() принимает свое наибольшее или наименьшее
значение на концах промежутка
принимает свое наибольшее или наименьшее
значение на концах промежутка
![]() .
Так, например, функция
.
Так, например, функция
![]() ,
рассматриваемая на промежутке
,
рассматриваемая на промежутке
![]() ,
принимает в точке
,
принимает в точке
![]() наименьшее значение, а в точке
наименьшее значение, а в точке
![]() — наибольшее значение. Однако
— наибольшее значение. Однако
![]() ,
,
![]() (см. рис. 4.10).
(см. рис. 4.10).
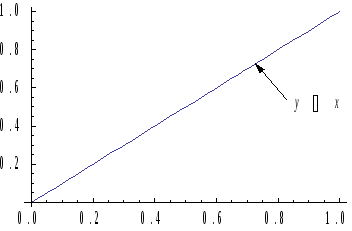
Рис. 4.10.
Теорема неприменима
и в том случае, когда функция
![]() принимает свое наибольшее или наименьшее
значение во внутренней точке с промежутка
принимает свое наибольшее или наименьшее
значение во внутренней точке с промежутка
![]() ,
но не имеет в точке с
определенной производной. Так, например,
функции
,
но не имеет в точке с
определенной производной. Так, например,
функции
![]() и
и
![]() ,
рассматриваемые в промежутке
,
рассматриваемые в промежутке
![]() принимают в точке
принимают в точке
![]() свое наименьшее значение. Однако, для
функции
свое наименьшее значение. Однако, для
функции
![]() имеем:
имеем:
![]() ,
,
![]() ,
а для функции
,
а для функции
![]() имеем:
имеем:
![]() ,
,
![]() (см. рис. 4.11 и 4.12).
(см. рис. 4.11 и 4.12).
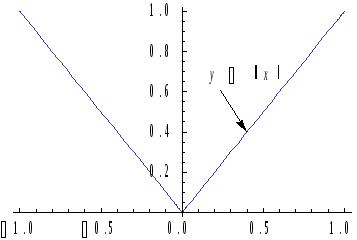
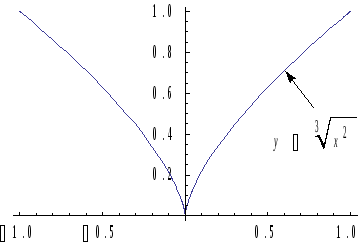
Рис. 4.11. Рис. 4.12.
2. Теорема Ролля.
Пусть функция
![]() удовлетворяет условиям:
удовлетворяет условиям:
-
 определена и
непрерывна на замкнутом промежутке
определена и
непрерывна на замкнутом промежутке
 ;
; -
 имеет определенную
производную
имеет определенную
производную
 хотя бы в открытом промежутке
хотя бы в открытом промежутке
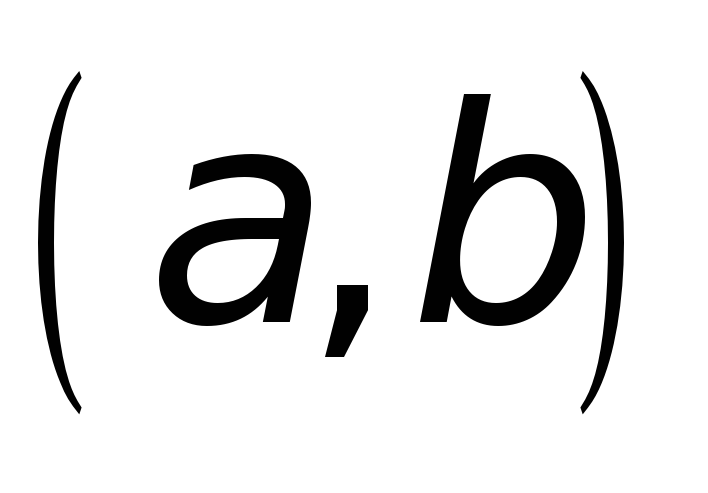 ;
; -
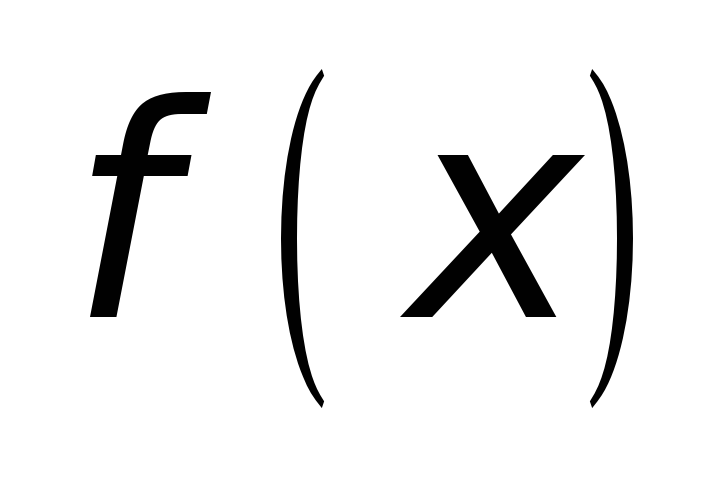 принимает равные
значения на концах промежутка, т. е.
принимает равные
значения на концах промежутка, т. е.
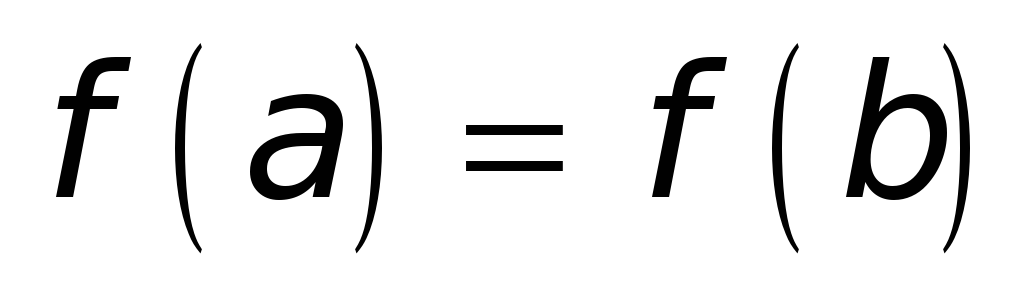 .
.
Тогда между точкой
а
и точкой b
найдется, по крайней мере, одна точка
с,
в которой производная функции обращается
в нуль, т.е.
![]() .
.
► По условию
функция
![]() определена и непрерывна в замкнутом
промежутке
определена и непрерывна в замкнутом
промежутке
![]() .
Значит,
.
Значит,
![]() достигает в этом промежутке как своего
наибольшего
достигает в этом промежутке как своего
наибольшего
![]() ,
так и своего наименьшего
,
так и своего наименьшего
![]() значений. Значит, для всех
значений. Значит, для всех
![]() будет:
будет:
![]() .
(1)
.
(1)
Могут реализоваться
два случая: 1)
![]() и 2)
и 2)
![]() .
.
1). Если
![]() ,
то из неравенства (1) следует, что все
значения
функции
,
то из неравенства (1) следует, что все
значения
функции
![]() в промежутке
в промежутке
![]() равны между собой, т. е.
равны между собой, т. е.
![]() ,
,
![]() ,
и, следовательно,
,
и, следовательно,
![]() для всех
для всех
![]() .
.
2). Если
![]() .
В этом случае хотя бы одно из двух
значений
.
В этом случае хотя бы одно из двух
значений
![]() или
или
![]() функция
функция
![]() принимает во внутренней точке с
промежутка
принимает во внутренней точке с
промежутка
![]() (так как иначе, ввиду того, что
(так как иначе, ввиду того, что
![]() ,
мы имели бы, что
,
мы имели бы, что
![]() ,
а это не так). Видим, что у нас выполнены
все условия теоремы Ферма. Значит,
,
а это не так). Видим, что у нас выполнены
все условия теоремы Ферма. Значит,
![]() .
◄
.
◄
Геометрически
теорема Ролля означает следующее: если
крайние ординаты графика функции
![]() равны, то на кривой обязательно найдется
точка, где касательная параллельна оси
Ох
(см. рис. 4.13).
равны, то на кривой обязательно найдется
точка, где касательная параллельна оси
Ох
(см. рис. 4.13).
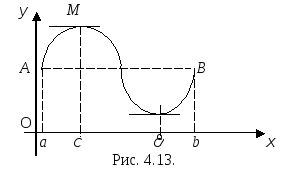
Обращаем внимание
на то, что непрерывность функции
![]() на замкнутом промежутке
на замкнутом промежутке
![]() и существование определенной производной
во всем открытом промежутке
и существование определенной производной
во всем открытом промежутке
![]() существенны для верности заключения
теоремы.
существенны для верности заключения
теоремы.
Функция
![]() в промежутке
в промежутке
![]() удовлетворяет всем условиям теоремы
Ролля, за исключением того, что имеет
разрыв в точке
удовлетворяет всем условиям теоремы
Ролля, за исключением того, что имеет
разрыв в точке
![]()
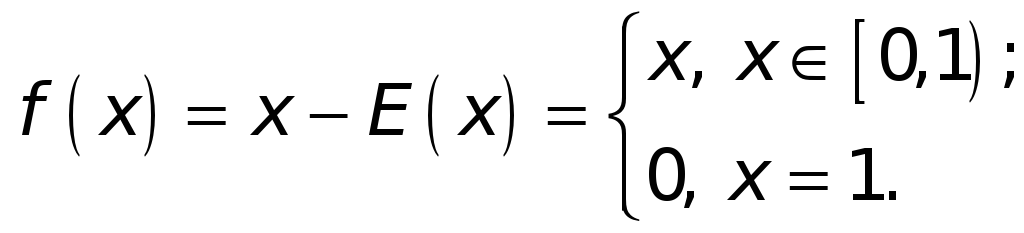
Имеем
![]() для всех
для всех
![]() ,
т. е.
,
т. е.
![]() не обращается в нуль ни в одной точке
промежутка
не обращается в нуль ни в одной точке
промежутка
![]() .
.
Функции
![]() и
и
![]() ,
рассматриваемые в промежутке
,
рассматриваемые в промежутке
![]() ,
удовлетворяют всем условиям теоремы
Ролля, за исключением того, что в точке
,
удовлетворяют всем условиям теоремы
Ролля, за исключением того, что в точке
![]() не имеют определенной (двусторонней)
производной.
не имеют определенной (двусторонней)
производной.
Для функции
![]() имеем:
имеем:
![]() ,
если
,
если
![]() ,
и
,
и
![]() ,
если
,
если
![]() =>
=>
![]() для
для
![]() .
.
Для функции
![]() имеем:
имеем:
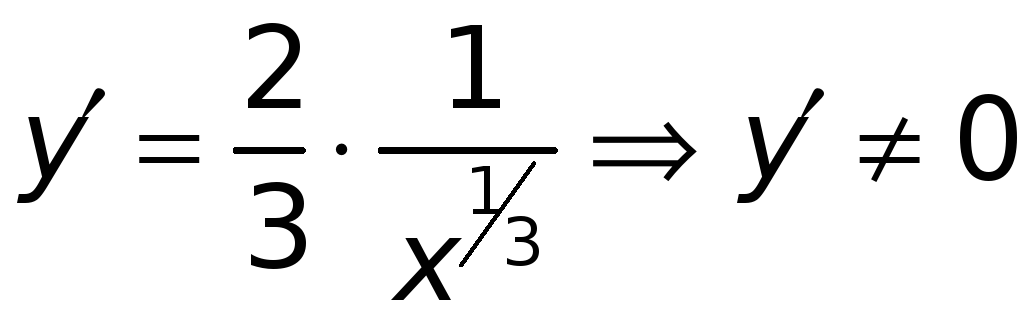 для
для
![]() (см. рис. 9 и 10).
(см. рис. 9 и 10).
Точно так же
существенно и условие 3) теоремы:
![]() .
Функция
.
Функция
![]() в промежутке
в промежутке
![]() ]
удовлетворяет всем условиям теоремы
Ролля, за исключением условия 3):
]
удовлетворяет всем условиям теоремы
Ролля, за исключением условия 3):
![]() .
Для функции
.
Для функции
![]() имеем:
имеем:
![]() для всех
для всех
![]() =>
=>
![]() не обращается в нуль ни в одной точке
промежутка
не обращается в нуль ни в одной точке
промежутка
![]() .
.
Частный случай
(теоремы Ролля).
Пусть функция
![]() удовлетворяет условиям:
удовлетворяет условиям:
-
 определена и
непрерывна на замкнутом промежутке
определена и
непрерывна на замкнутом промежутке
 ;
; -
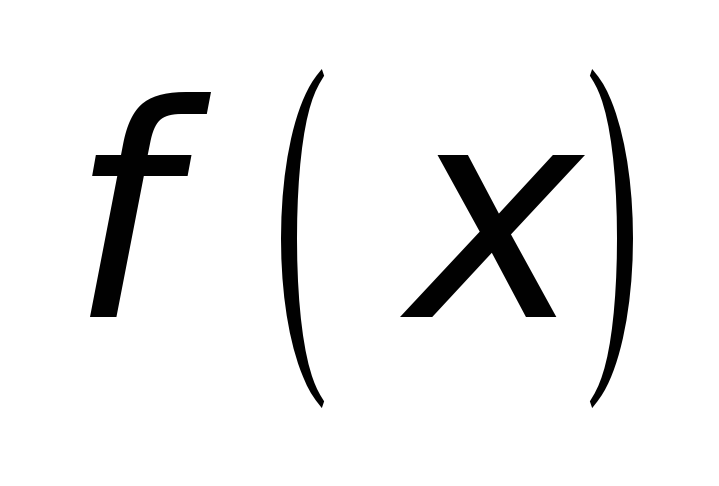 дифференцируема
во всех точках в открытого промежутка
дифференцируема
во всех точках в открытого промежутка
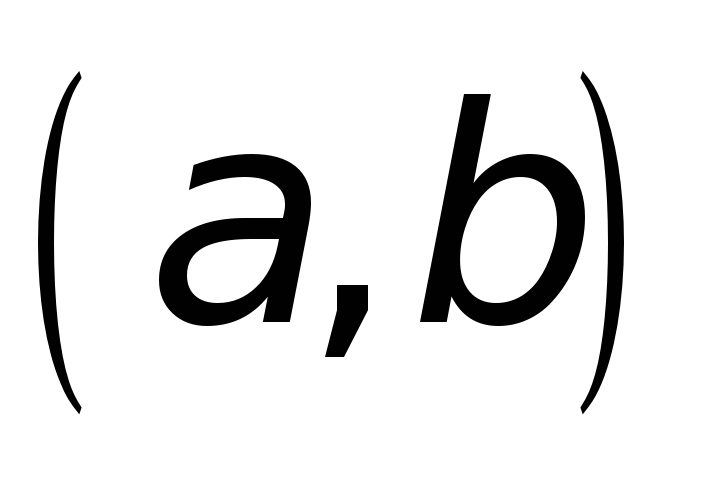 ;
; -
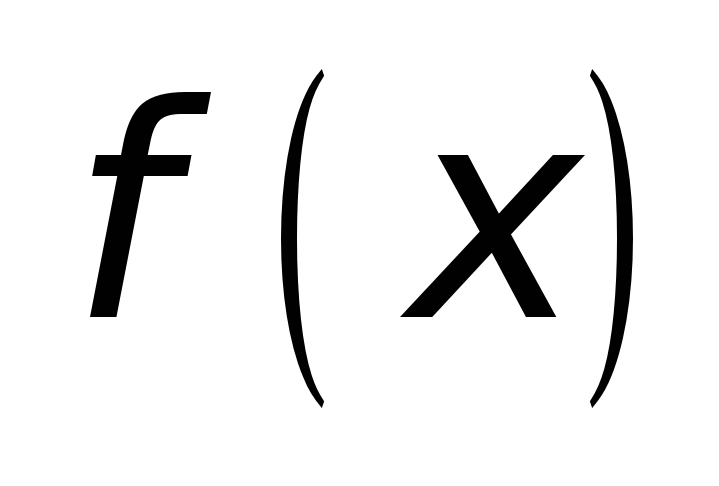 обращается в нуль
на концах промежутка
обращается в нуль
на концах промежутка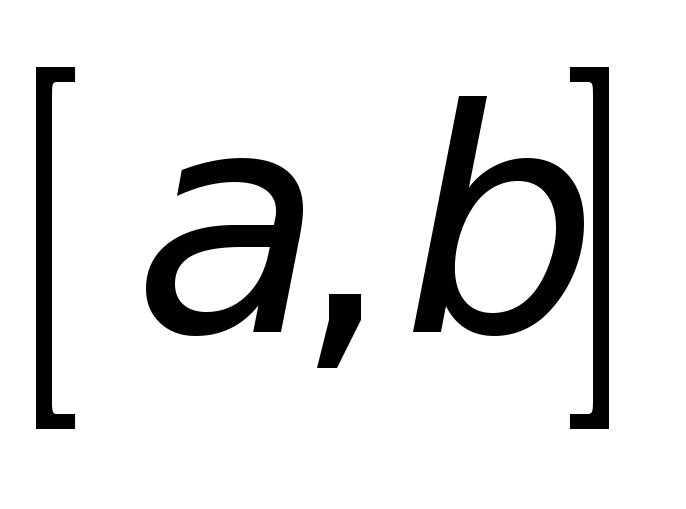 ,
т. е.
,
т. е.
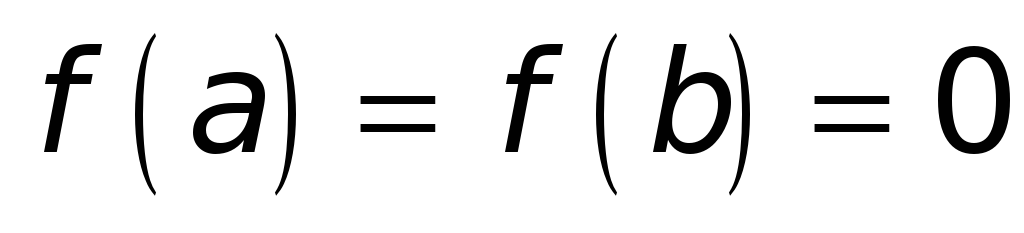 .
.
Тогда существует
хотя бы одна точка
![]() ,
в которой производная
,
в которой производная
![]() обращается в нуль.
обращается в нуль.
Короче: между двумя нулями дифференцируемой функции всегда лежит хотя бы один нуль ее производной.
3. Теорема Лагранжа.
Пусть функция
![]() удовлетворяет условиям:
удовлетворяет условиям:
-
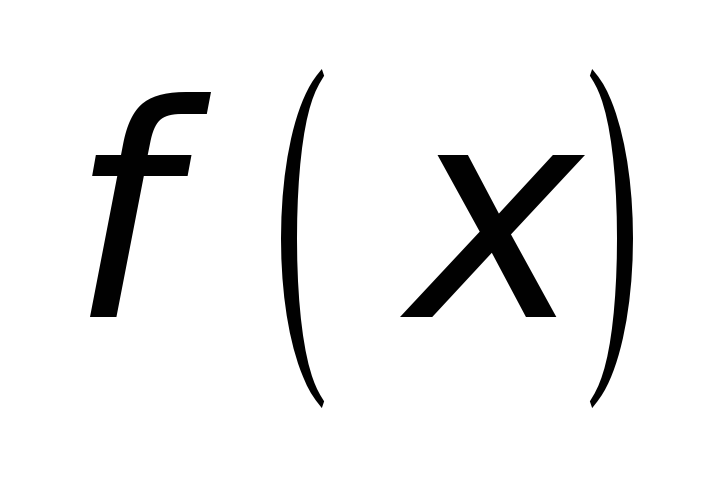 определена и
непрерывна на замкнутом промежутке
определена и
непрерывна на замкнутом промежутке
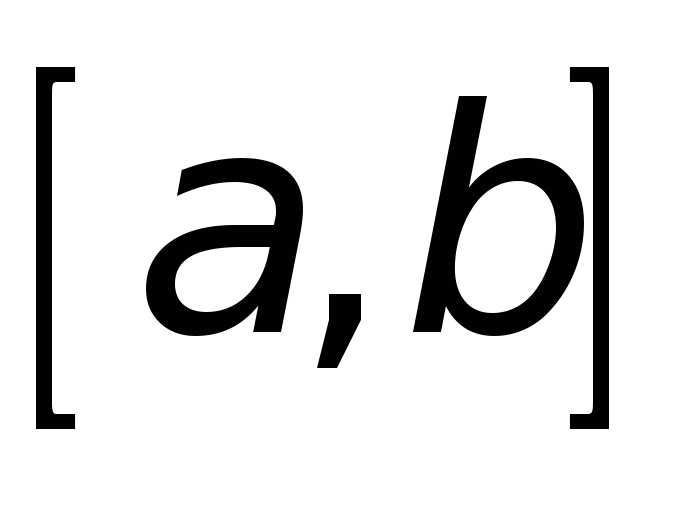 ;
; -
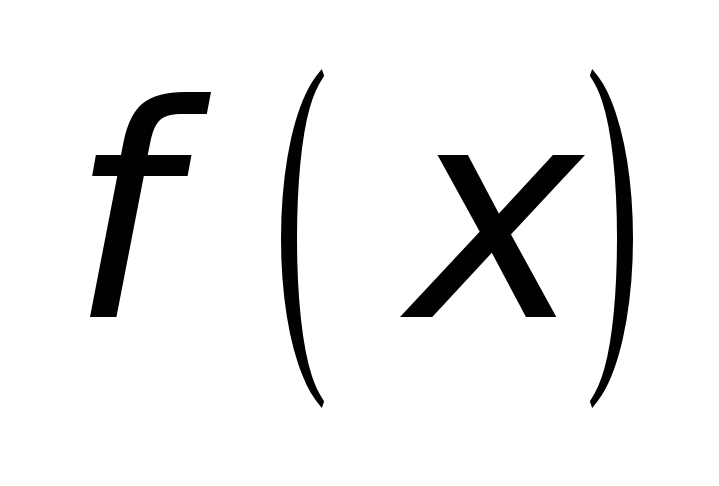 имеет определенную
производную
имеет определенную
производную
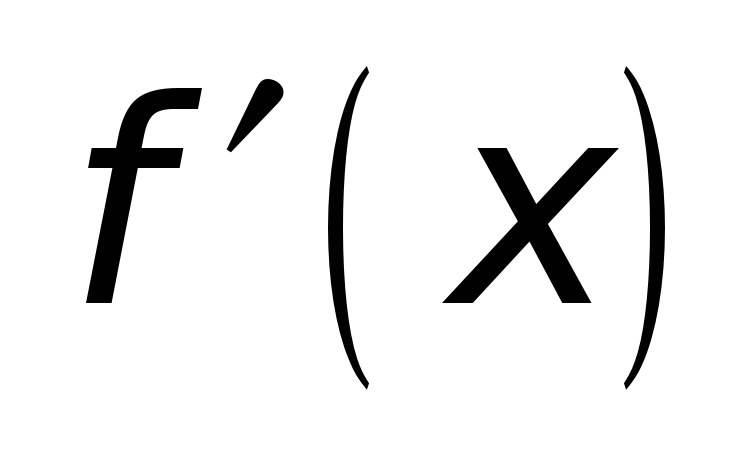 хотя бы в открытом промежутке
хотя бы в открытом промежутке
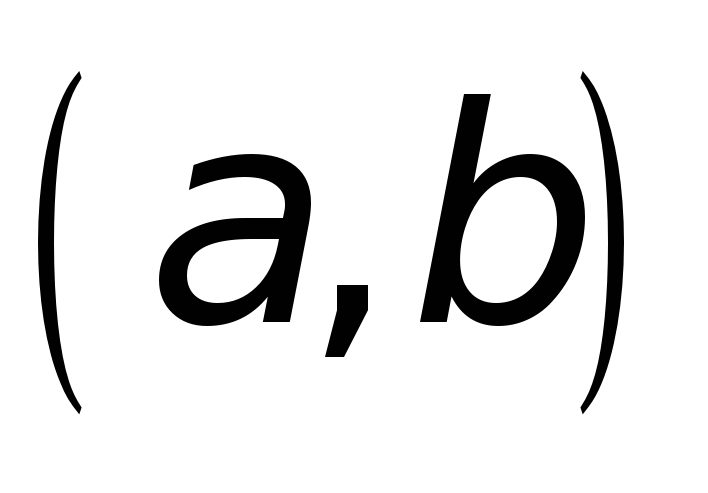 ;
;
Тогда между точкой а и точкой b найдется, по крайней мере, одна точка с такая, в которой имеет место равенство:
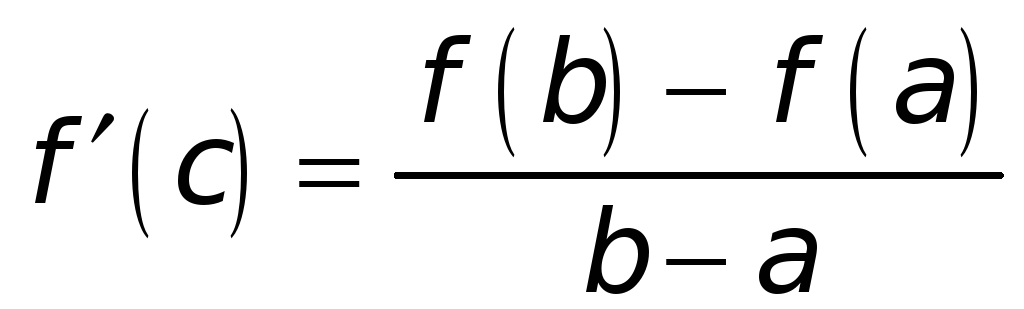 .
.
► Для доказательства введем в рассмотрение вспомогательную Функцию
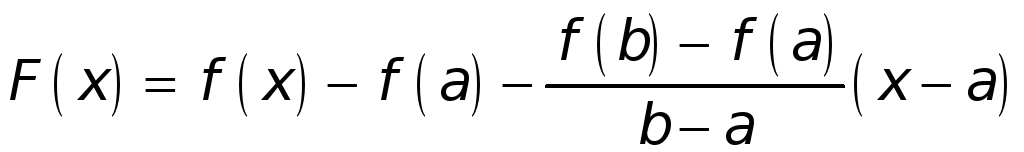 .
.
Отметим, что:
-
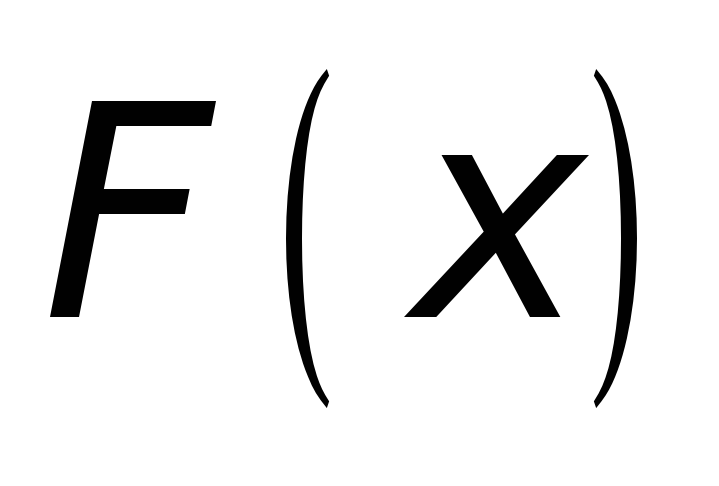 определена и
непрерывна на замкнутом промежутке
определена и
непрерывна на замкнутом промежутке
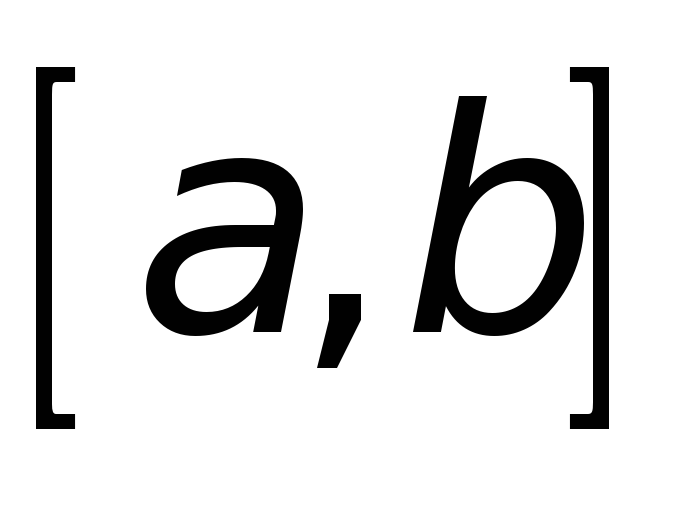 ,
ибо
,
ибо
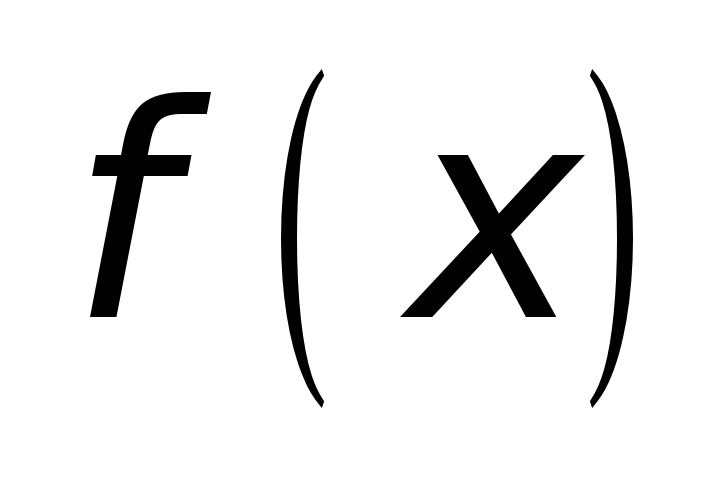 определена и непрерывна на
определена и непрерывна на
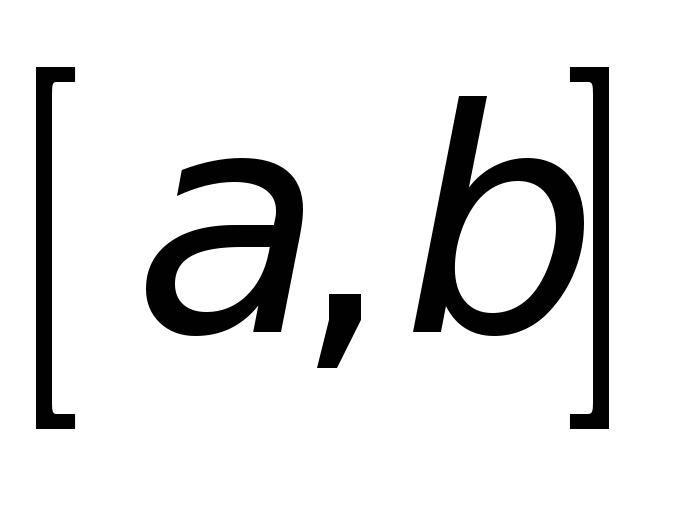 ;
; -
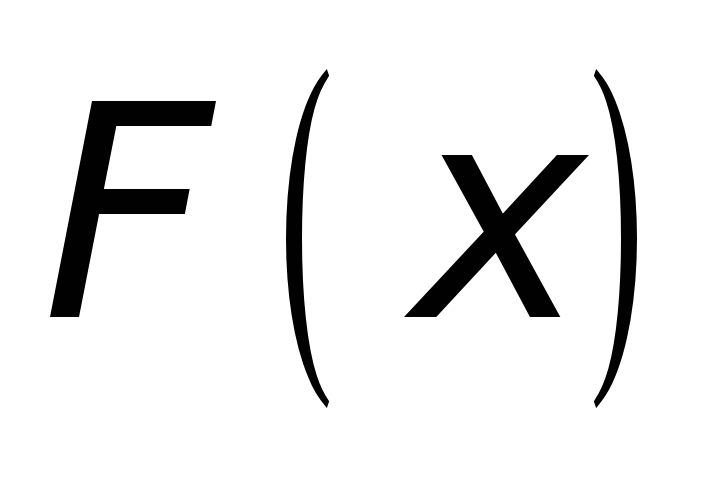 имеет определенную
производную
имеет определенную
производную
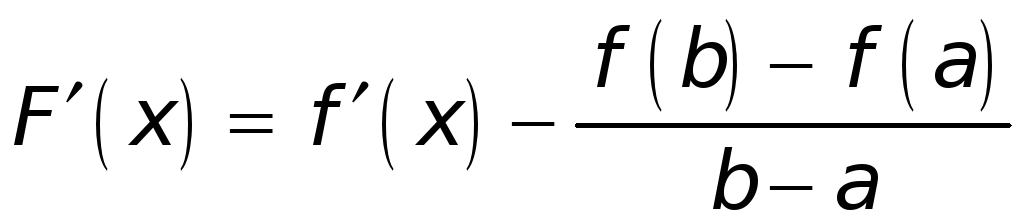
хотя бы в открытом
промежутке
![]() , ибо в
, ибо в
![]() существует определенная производная
существует определенная производная
![]() ;
;
-
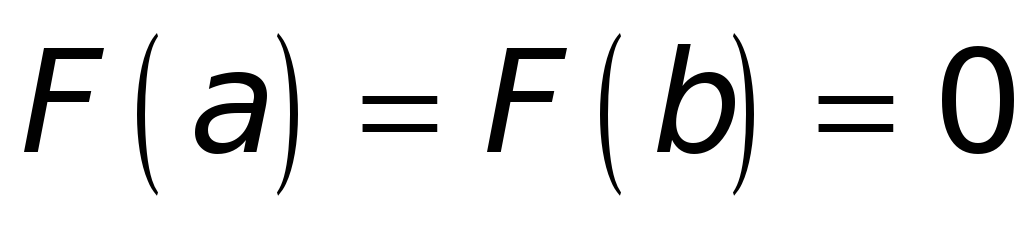 .
.
Видим, что функция
![]() удовлетворяет всем трем условиям теоремы
Ролля. Следовательно, между точкой а
и точкой b
обязательно найдется хотя бы одна точка
с
такая, что будет
удовлетворяет всем трем условиям теоремы
Ролля. Следовательно, между точкой а
и точкой b
обязательно найдется хотя бы одна точка
с
такая, что будет
![]() ,
т. е.
,
т. е.
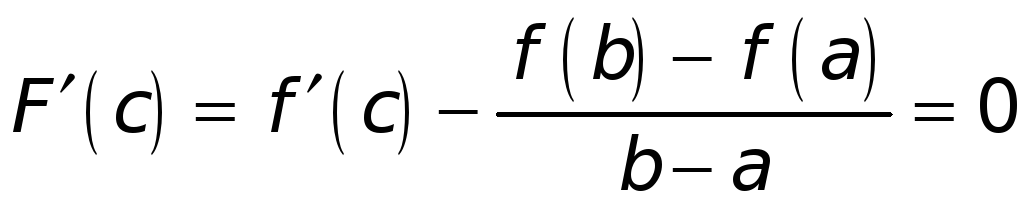 ,
,
а значит,
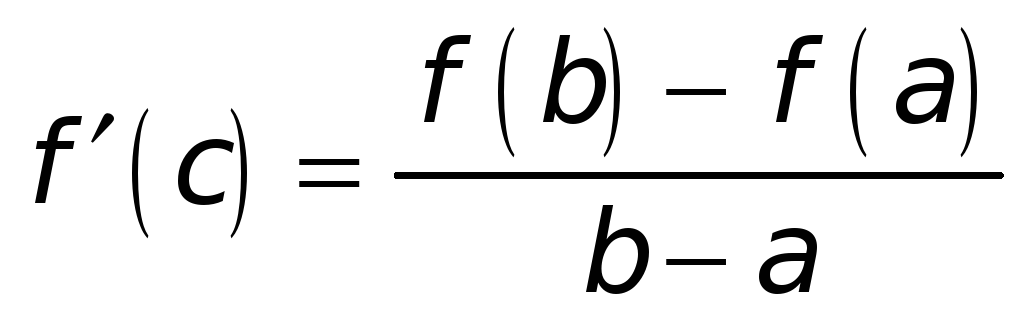 .
◄
.
◄
Полученную формулу называют формулой конечных приращений Лагранжа. Приведем другие формы записи формулы Лагранжа.
1.
![]() ,
где
,
где
![]() .
(*)
.
(*)
Заметим, что формуле (*) можно придать и такой вид:
![]() ,
,
откуда следует
несущественность того, будет ли
![]() или, наоборот,
или, наоборот,
![]() .
.
2. Пусть
![]() .
Из каждого члена этого неравенства
вычтем а.
Получим
.
Из каждого члена этого неравенства
вычтем а.
Получим
![]() .
Так как
.
Так как
![]() ,
то все члены последнего неравенства
можно поделить на
,
то все члены последнего неравенства
можно поделить на
![]() .
Будем иметь
.
Будем иметь
![]() .
.
Обозначим
![]() (это — обычное обозначение величины,
лежащей между 0 и 1). Отсюда
(это — обычное обозначение величины,
лежащей между 0 и 1). Отсюда
![]() .
Поэтому формулу Лагранжа можно записать
в виде
.
Поэтому формулу Лагранжа можно записать
в виде
![]() .
.
3. Рассмотрим
промежуток
![]() ,
т. е. положим
,
т. е. положим
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
и формула Лагранжа запишется в виде
,
и формула Лагранжа запишется в виде
![]() .
.
Следствие из
теоремы Лагранжа.
Пусть функция
![]() определена и непрерывна в окрестности
определена и непрерывна в окрестности
![]() точки
точки
![]() .
Пусть
.
Пусть
![]() имеет конечную производную
имеет конечную производную
![]() в проколотой окрестности
в проколотой окрестности
![]() точки
точки
![]() .
Тогда, если существует конечный или
бесконечный предел
.
Тогда, если существует конечный или
бесконечный предел
![]() ,
то существует и производная
,
то существует и производная
![]() ,
равная этому пределу.
,
равная этому пределу.
► Дадим
![]() приращение
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
В промежутке
.
В промежутке
![]() применим к функции
применим к функции
![]() теорему Лагранжа. Будем иметь
теорему Лагранжа. Будем иметь
![]() ,
,
откуда
![]() .
.
Если положить
![]() ,
то очевидно, что
,
то очевидно, что
![]() ,
если
,
если
![]() ,
причем
,
причем
![]() .
Поэтому
.
Поэтому
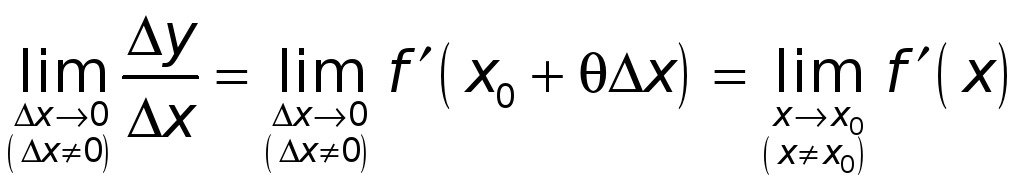 .
.
Это означает, что
![]() существует, и справедливо равенство
существует, и справедливо равенство
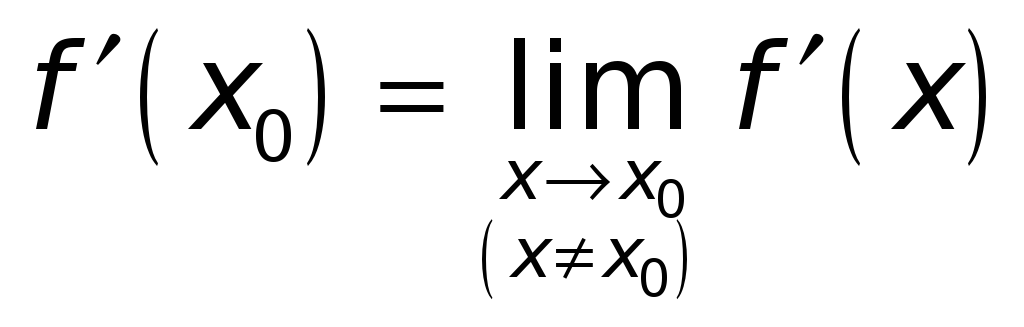 .
◄
.
◄
4. Теорема Коши.
Пусть имеются две функции
![]() и
и
![]() ,
удовлетворяющие следующим условиям:
,
удовлетворяющие следующим условиям:
-
 и
и
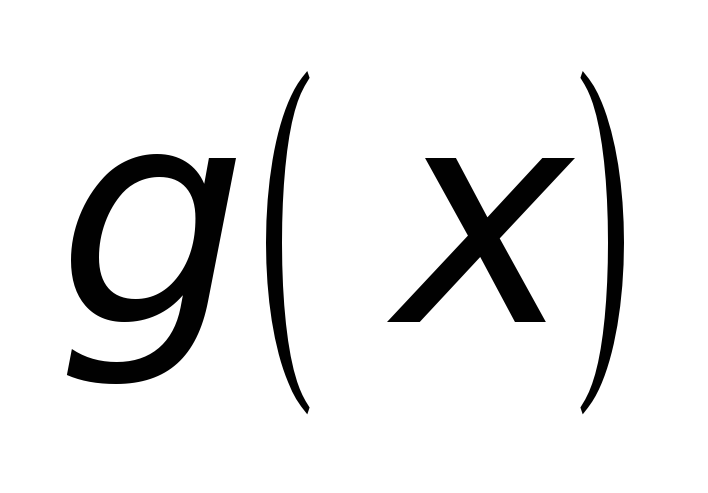 определены и непрерывны на замкнутом
промежутке
определены и непрерывны на замкнутом
промежутке
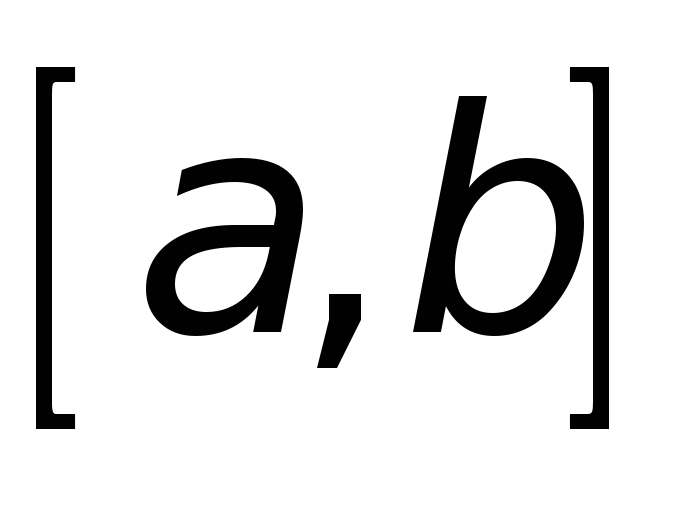 ;
; -
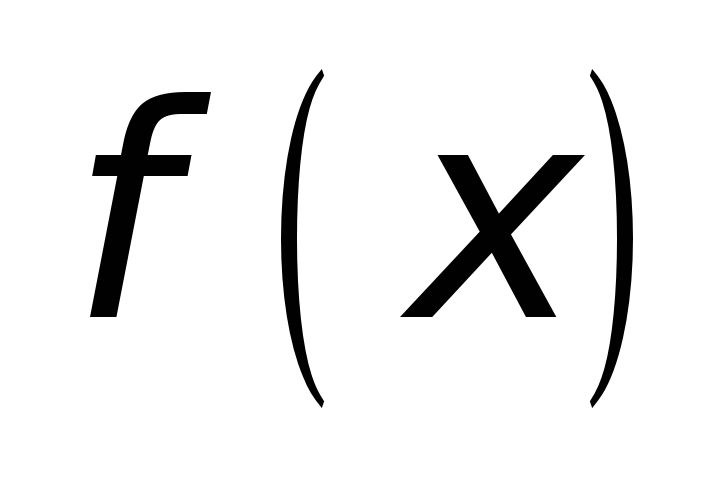 и
и
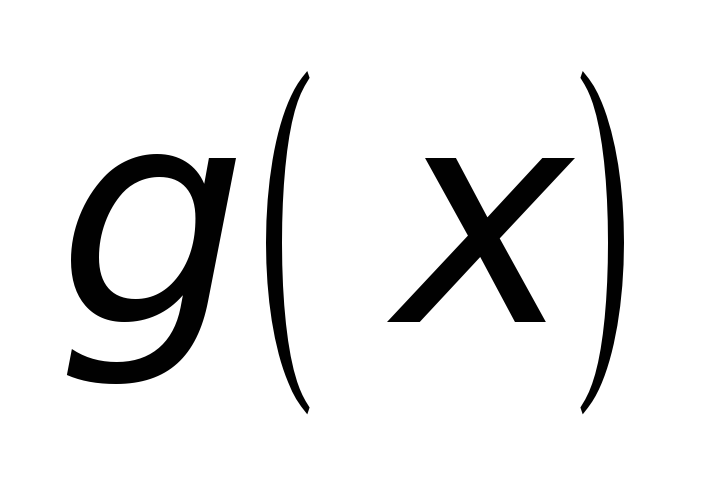 имеют конечные производные
имеют конечные производные
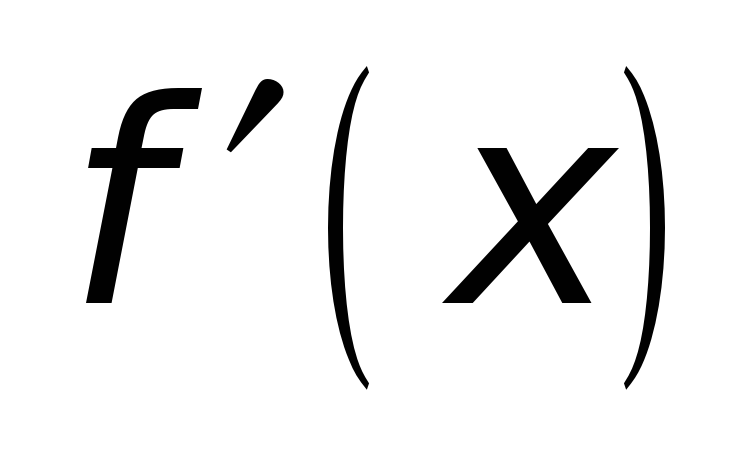 и
и
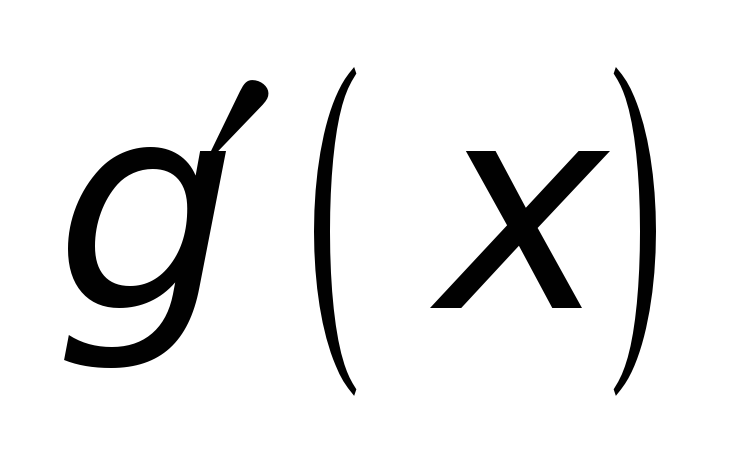 хотя бы в открытом промежутке
хотя бы в открытом промежутке
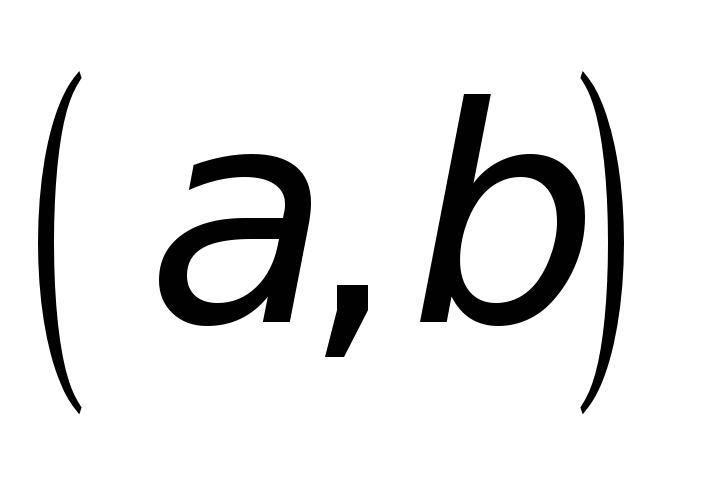 ;
; -
для всех
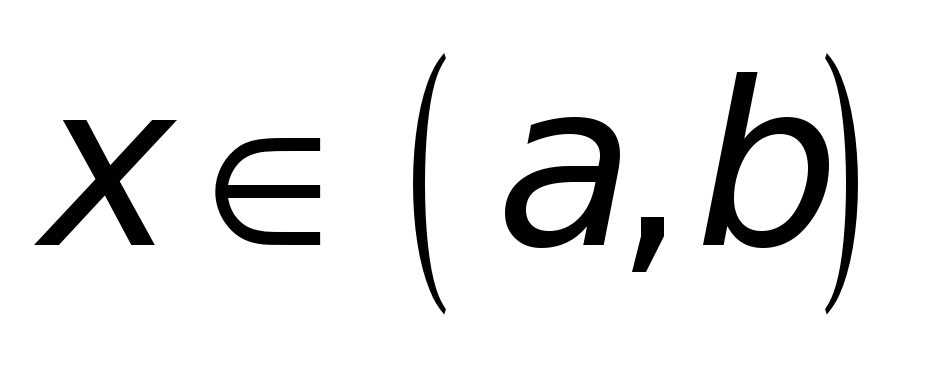 :
:
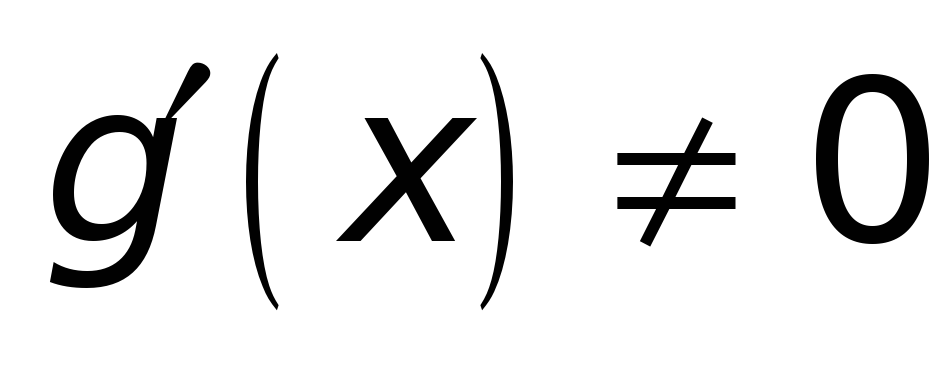 .
.
Тогда между точками а и b обязательно найдется по крайней мере одна точка с такая, в которой имеет место равенство
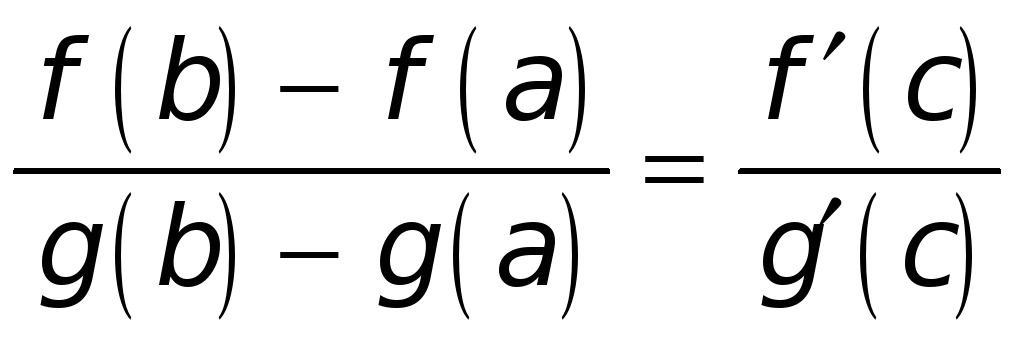 .
.
► Заметим сначала,
что
![]() .
Действительно, если предположить, что
.
Действительно, если предположить, что
![]() ,
то функция g(x)
будет удовлетворять всем трем условиям
теоремы Ролля, и тогда по этой теореме
между точками a
и b обязательно найдется хотя бы одна
точка
,
то функция g(x)
будет удовлетворять всем трем условиям
теоремы Ролля, и тогда по этой теореме
между точками a
и b обязательно найдется хотя бы одна
точка
![]() такая, что будет
такая, что будет
![]() .
А это невозможно, ибо по условию
.
А это невозможно, ибо по условию
![]() для всех
для всех
![]() .
.
Введем в рассмотрение вспомогательную функцию
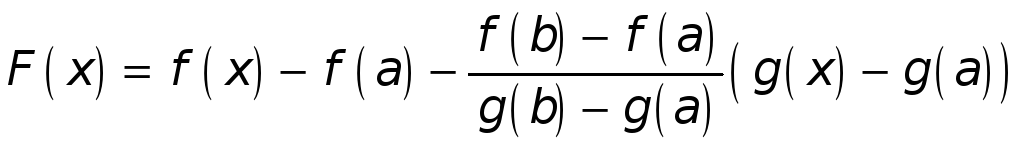 .
(*)
.
(*)
Замечаем, что:
1)
![]() определена и непрерывна на замкнутом
промежутке
определена и непрерывна на замкнутом
промежутке
![]() ,
ибо
,
ибо
![]() и
и
![]() определены и непрерывны на
определены и непрерывны на
![]()
2)
![]() имеет конечную производную
имеет конечную производную
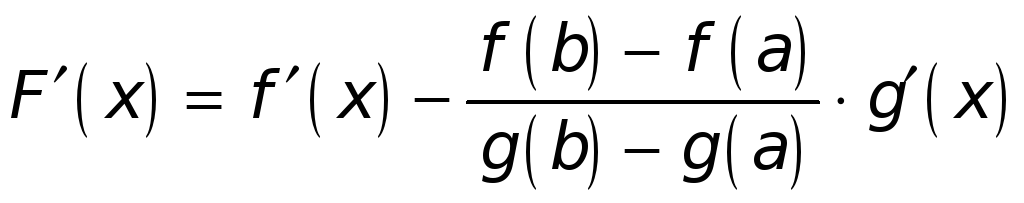
хотя бы в открытом
промежутке
![]() ,
ибо в
,
ибо в
![]() существуют конечные производные
существуют конечные производные
![]() и
и
![]() ;
;
3)
![]() (в этом убеждаемся непосредственной
подстановкой в выражение (*) для
(в этом убеждаемся непосредственной
подстановкой в выражение (*) для
![]() значений
значений
![]() и
и
![]() ).
).
Видим, что функция
![]() удовлетворяет всем трем условиям теоремы
Ролля. Следовательно, между точками а
и b
обязательно найдется хотя бы одна точка
с
такая, что будет
удовлетворяет всем трем условиям теоремы
Ролля. Следовательно, между точками а
и b
обязательно найдется хотя бы одна точка
с
такая, что будет
![]() ,
т. е.
,
т. е.
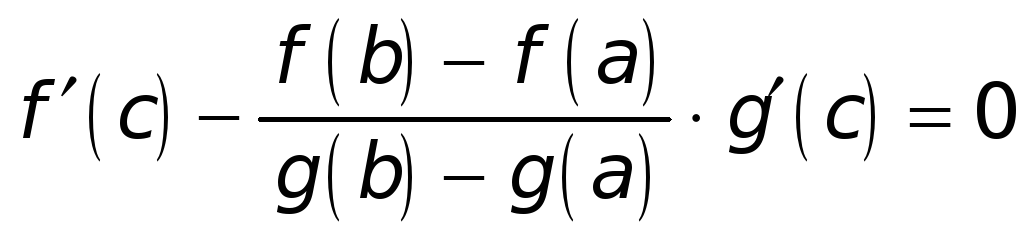 ,
,
а значит,
 .
◄
.
◄
Установленная формула называется формулой Коши.
Замечание 1.
В условии 2) теоремы можно допустить,
что
![]() и
и
![]() могут принимать в промежутке
могут принимать в промежутке
![]() и бесконечные, но определенного знака,
значения. Только эти бесконечные значения
они не должны принимать в одной и той
же точке.
и бесконечные, но определенного знака,
значения. Только эти бесконечные значения
они не должны принимать в одной и той
же точке.
Замечание 2.
Формула конечных приращений Лагранжа
является частным случаем формулы Коши,
когда
![]() ,
,
![]() .
.
Замечание 3.
Формула Коши, так же как и формула
Лагранжа, имеет место не только когда
![]() ,
но и в случае, когда
,
но и в случае, когда
![]() .
.
