
- •Глава 4 Производная и дифференциал § 1. Производная. Механический и геометрический смысл производной
- •4. Односторонние производные.
- •§2. Понятие дифференцируемости функции
- •§ 3. Формулы и правила вычисления производных
- •7. Простейшие правила вычисления производных.
- •12. Формула для приращения функции.
- •13. Правило дифференцирования сложной функции.
- •14. Правила дифференцирования обратных функций.
- •§ 4. Дифференциал функции
- •2. Геометрический смысл дифференциала.
- •3. Сводка формул для дифференциалов.
- •4. Дифференциал сложной функции. Инвариантность формы дифференциала.
- •§ 5. Производные высших порядков
- •2. Формула Лейбница для производной n-го порядка от произведения двух функций.
- •3. Механическое истолкование второй производной.
- •§ 6. Дифференциалы высших порядков
- •§ 7. Дифференцирование функции, заданной параметрически
- •§ 8. Основные теоремы дифференциального исчисления
- •§ 9. Формула Тейлора
- •2. Примеры разложения по формуле Тейлора.
- •§ 10. Раскрытие неопределенностей по правилу Лопиталя
- •1. Неопределенность вида .
- •2. Неопределенность вида .
- •§ 11. Признаки постоянства, возрастания и убывания функций
- •§ 12. Теория экстремальных значений функции
- •2. Исследование стационарных критических точек функции с помощью второй производной.
- •§ 13. Характер выпуклости кривой. Точки перегиба
- •§ 14. Асимптоты кривой
- •§ 15. Построение графика функции по характерным точкам
2. Неопределенность вида .
Теорема 2.
Пусть функции
![]() и
и
![]() :
:
1) определены в
промежутке
![]() (а
— конечное число,
(а
— конечное число,
![]() );
);
2) имеют конечные
производные
![]() и
и
![]() в
в
![]() ,
причем
,
причем
![]() в
в
![]() ;
;
3) ![]() ;
;
![]() .
.
Тогда, если существует конечный или бесконечный (определенного знака) предел
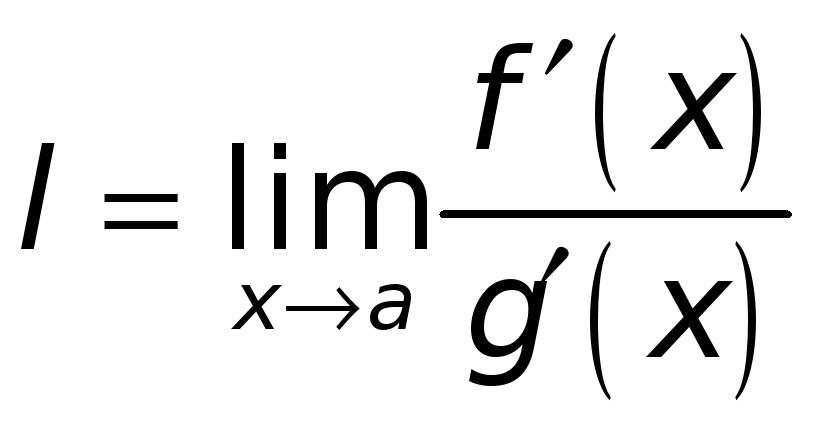 ,
,
то к тому же пределу
![]() при
при
![]() стремится и отношение
стремится и отношение
![]() (т.е.
(т.е.
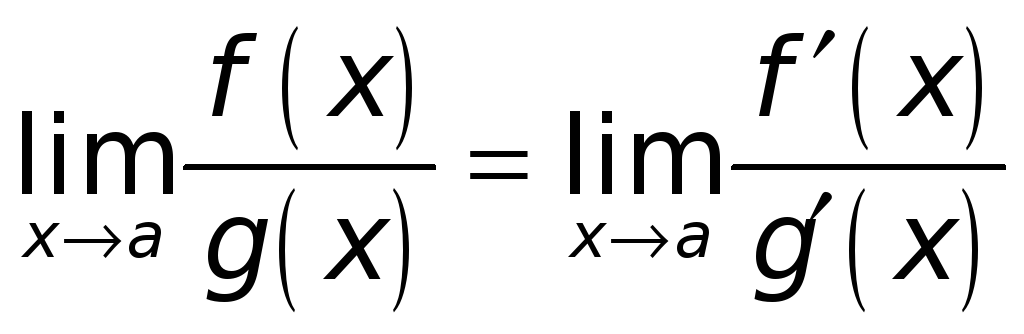 ).
).
Замечание.
Здесь не исключаются случаи, когда
![]() — несобственное число
— несобственное число
![]() .
.
Замечание. И в этом случае, если не существует предел отношения производных, то это вовсе не означает, что не существует и предел отношения самих функций.
(Принимаем без доказательства.)
§ 11. Признаки постоянства, возрастания и убывания функций
Теорема 1 (признак
постоянства функции).
Пусть функция
![]() определена и непрерывна в некотором
промежутке Х
и имеет внутри этого промежутка конечную
производную
определена и непрерывна в некотором
промежутке Х
и имеет внутри этого промежутка конечную
производную
![]() .
Для того, чтобы
.
Для того, чтобы
![]() имела в промежутке
имела в промежутке
![]() постоянное значение, необходимо и
достаточно, чтобы во всех точках х,
лежащих внутри X,
было:
постоянное значение, необходимо и
достаточно, чтобы во всех точках х,
лежащих внутри X,
было:
![]() .
.
► Необходимость.
Пусть
![]() .
Тогда для любого х,
лежащего внутри X,
будет
.
Тогда для любого х,
лежащего внутри X,
будет
![]() .
.
Достаточность.
Дано:
![]() для всех х,
лежащих внутри X.
Требуется доказать, что
для всех х,
лежащих внутри X.
Требуется доказать, что
![]() .
Возьмем в промежутке любую точку х0
и закрепим ее. Пусть х
— любая другая точка из промежутка X.
.
Возьмем в промежутке любую точку х0
и закрепим ее. Пусть х
— любая другая точка из промежутка X.
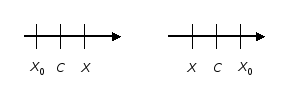
Замечаем, что в
промежутке
![]() функция
функция
![]() удовлетворяет всем условиям теоремы
Лагранжа. Но тогда между точками х0
и х
обязательно найдется точка с
такая, что будет
удовлетворяет всем условиям теоремы
Лагранжа. Но тогда между точками х0
и х
обязательно найдется точка с
такая, что будет
![]() .
(1)
.
(1)
Так как точка с
лежит между точками х0
и х,
то точка с
лежит внутри промежутка X.
По условию
![]() для всех х,
лежащих внутри X.
Значит, в частности,
для всех х,
лежащих внутри X.
Значит, в частности,
![]() .
А тогда из (1) получаем
.
А тогда из (1) получаем
![]() ,
т. e.
,
т. e.
![]() .
(2)
.
(2)
Так как в соотношении
(2) точка х
— любая из промежутка X,
то заключаем, что
![]() .
◄
.
◄
Следствие.
Пусть имеются две функции
![]() и
и
![]() ,
и пусть:
,
и пусть:
1)
![]() и
и
![]() определены и непрерывны в промежутке
X;
определены и непрерывны в промежутке
X;
2)
![]() и
и
![]() имеют внутри промежутка X
конечные производные
имеют внутри промежутка X
конечные производные
![]() и
и
![]() ;
;
3) во всех точках
х
внутри промежутка X:
![]() .
.
Тогда во всем
промежутке X
функции
![]() и
и
![]() отличаются друг от друга на постоянную
величину.
отличаются друг от друга на постоянную
величину.
► Введем в
рассмотрение функцию
![]() .
Имеем:
.
Имеем:
-
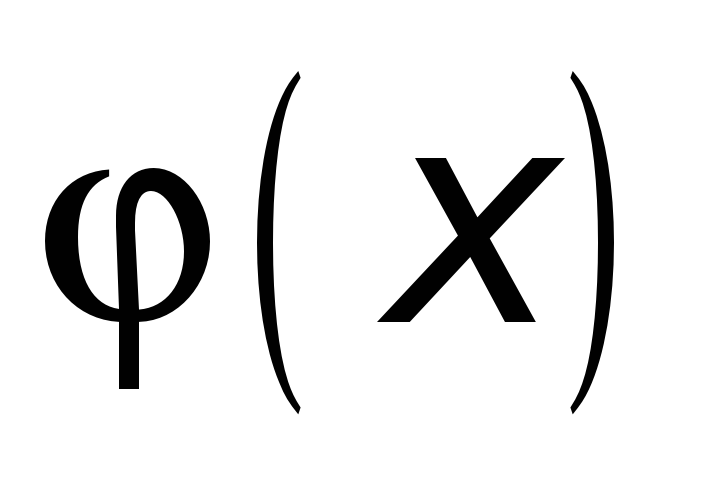 определена и
непрерывна в промежутке X;
определена и
непрерывна в промежутке X; -
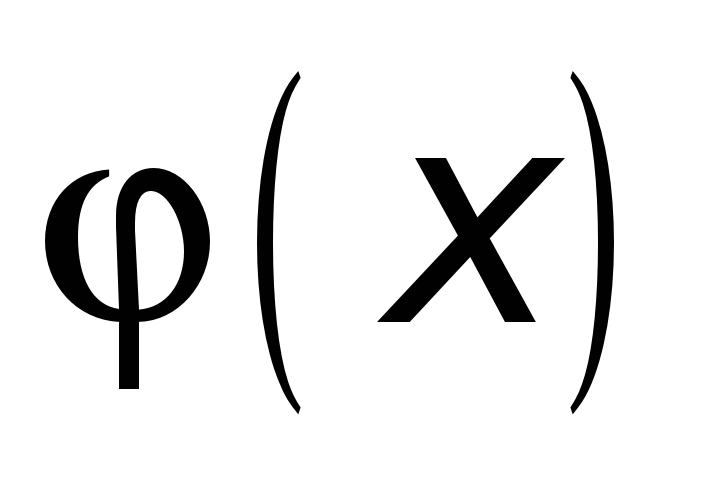 имеет внутри X
конечную производную
имеет внутри X
конечную производную
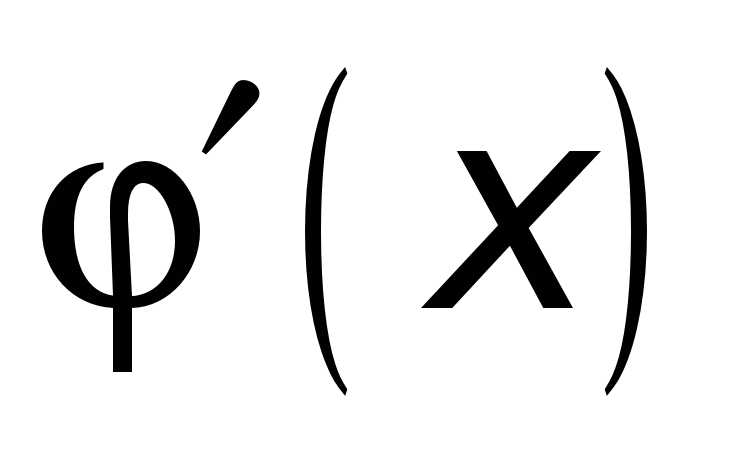 ;
; -
во всех точках х внутри X:
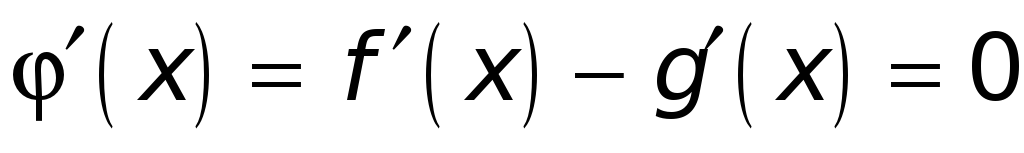 .
.
Видим, что функция
![]() удовлетворяет всем условиям теоремы
1. Следовательно,
удовлетворяет всем условиям теоремы
1. Следовательно,
![]() ,
,
![]() ,
т. е.
,
т. е.
![]() ,
,
![]() .
◄
.
◄
Теорема 2 (признак возрастания и убывания функции в широком смысле). Пусть:
1) функция
![]() определена и непрерывна в промежутке
X;
определена и непрерывна в промежутке
X;
2)
![]() имеет внутри промежутка X
конечную или бесконечную (определенного
знака) производную
имеет внутри промежутка X
конечную или бесконечную (определенного
знака) производную
![]() .
.
При этих условиях:
I. Для того чтобы
![]() была возрастающей (в широком смысле) в
промежутке X,
необходимо и достаточно, чтобы для всех
х
внутри X
было:
была возрастающей (в широком смысле) в
промежутке X,
необходимо и достаточно, чтобы для всех
х
внутри X
было:
![]() .
.
II. Для того чтобы
![]() была убывающей (в широком смысле) в
промежутке X,
необходимо и достаточно, чтобы для всех
х
внутри X
было:
была убывающей (в широком смысле) в
промежутке X,
необходимо и достаточно, чтобы для всех
х
внутри X
было:
![]() .
.
► Докажем утверждение I (утверждение II доказывается аналогично).
Необходимость.
Дано: функция
![]() в промежутке
в промежутке
![]() возрастает (в широком смысле). Требуется
доказать, что
возрастает (в широком смысле). Требуется
доказать, что
![]() внутри промежутка X.
внутри промежутка X.
Возьмем внутри
промежутка X
любую точку х.
Дадим этому х
приращение
![]() — любое, но такое, что
— любое, но такое, что
![]() и точка
и точка
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
а значит,
,
а значит,
![]() ,
т. е.
,
т. е.
![]() .
Но тогда
.
Но тогда
![]() ,
и, следовательно,
,
и, следовательно,
![]() ,
т. е.
,
т. е.
![]() .
.
Если
![]() ,
то
,
то
![]() ,
а значит,
,
а значит,
![]() .
Но тогда
.
Но тогда
![]() ,
и, следовательно,
,
и, следовательно,
![]() ,
т. е.
,
т. е.
![]() .
.
По условию в точке
х
существует производная функции
![]() в обычном смысле. Следовательно,
в обычном смысле. Следовательно,
![]() .
Значит,
.
Значит,
![]() .
Так как точка х
была любой, лежащей внутри X,
то заключаем, что
.
Так как точка х
была любой, лежащей внутри X,
то заключаем, что
![]() внутри промежутка X.
внутри промежутка X.
Достаточность.
Дано:
![]() внутри промежутка X.
Требуется доказать, что
внутри промежутка X.
Требуется доказать, что
![]() возрастает (в широком смысле) в промежутке
X.
возрастает (в широком смысле) в промежутке
X.
В промежутке X
возьмем две точки
![]() и
и
![]() — любые, но такие, что
— любые, но такие, что
![]() .
Рассмотрим промежуток
.
Рассмотрим промежуток
![]() .
Заметим, что
.
Заметим, что
![]() и что на промежутке
и что на промежутке
![]() функция
функция
![]() удовлетворяет условиям теоремы Лагранжа.
(
удовлетворяет условиям теоремы Лагранжа.
(![]() определена и непрерывна на
определена и непрерывна на
![]() и имеет в промежутке
и имеет в промежутке
![]() конечную или бесконечную определенного
знака производную
конечную или бесконечную определенного
знака производную
![]() .)
По теореме Лагранжа, имеем
.)
По теореме Лагранжа, имеем
![]() ,
где
,
где
![]() — некоторая точка из
— некоторая точка из
![]() .
Так как по условию
.
Так как по условию
![]() и так как
и так как
![]() ,
то
,
то
![]() ,
т. е.
,
т. е.
![]() .
.
Итак, для любых
двух точек
![]() и
и
![]() из X,
из того, что
из X,
из того, что
![]() ,
следует, что
,
следует, что
![]() .
Значит, функция
.
Значит, функция
![]() возрастает (в широком смысле) в промежутке
X.
◄
возрастает (в широком смысле) в промежутке
X.
◄
Теорема 3 (признак строгого возрастания и строгого убывания функции). Пусть:
1) функция
![]() определена и непрерывна в промежутке
X;
определена и непрерывна в промежутке
X;
2)
![]() имеет внутри промежутка X
конечную или бесконечную (определенного
знака) производную
имеет внутри промежутка X
конечную или бесконечную (определенного
знака) производную
![]() .
.
При этих условиях:
I. Для того чтобы
![]() была строго возрастающей в промежутке
X,
необходимо и достаточно выполнение еще
следующих двух условий:
была строго возрастающей в промежутке
X,
необходимо и достаточно выполнение еще
следующих двух условий:
а) для всех х
внутри X
должно быть
![]() ;
;
б) внутри X
не существует такого интервала
![]() ,
во всех точках которого
,
во всех точках которого
![]() .
.
П. Для того, чтобы
![]() была строго убывающей в промежутке X,
необходимо и достаточно выполнение еще
следующих двух условий:
была строго убывающей в промежутке X,
необходимо и достаточно выполнение еще
следующих двух условий:
а) для всех х
внутри
![]() должно быть
должно быть
![]() ;
;
б) внутри Х
не существует такого интервала
![]() ,
во всех точках которого
,
во всех точках которого
![]() .
.
Докажем утверждение I (утверждение II доказывается аналогично).
► Необходимость.
Дано: функция
![]() строго возрастающая в промежутке X.
Требуется доказать необходимость
выполнения условий а) и б).
строго возрастающая в промежутке X.
Требуется доказать необходимость
выполнения условий а) и б).
Необходимость условия а) показывается так же, как и при доказательстве теоремы 2. Установим необходимость условия б).
Предположим, что
условие б) не выполнено. Но тогда внутри
X
существует промежуток
![]() ,
во всех точках которого
,
во всех точках которого
![]() и, следовательно, по теореме 1 будет
и, следовательно, по теореме 1 будет
![]() для
для
![]() ,
т. е.
,
т. е.
![]() не будет строго возрастающей в промежутке
не будет строго возрастающей в промежутке
![]() (ибо, например,
(ибо, например,
![]() ,
a
,
a
![]() ).
).
Вывод:
выполнение условия б) необходимо для
строгого возрастания функции
![]() в промежутке X.
в промежутке X.
Достаточность.
Дано: для функции
![]() выполнены условия а) и б). Требуется
доказать, что
выполнены условия а) и б). Требуется
доказать, что
![]() строго возрастающая в промежутке X.
строго возрастающая в промежутке X.
Если выполнено
условие а), то по теореме 2 функция
![]() возрастает (по крайней мере, в широком
смысле) в промежутке X.
Надо показать теперь, что выполнение
еще и условия б) обеспечивает строгое
возрастание
возрастает (по крайней мере, в широком
смысле) в промежутке X.
Надо показать теперь, что выполнение
еще и условия б) обеспечивает строгое
возрастание
![]() в промежутке X.
в промежутке X.
Рассуждаем от
противного. Предположим, что несмотря
на выполнение условий а) и б) в промежутке
X
имеются точки
![]() и
и
![]() (пусть, для определенности,
(пусть, для определенности,
![]() )
такие, что
)
такие, что
![]() .
Возьмем любое х,
удовлетворяющее условию:
.
Возьмем любое х,
удовлетворяющее условию:
![]() .
Так как
.
Так как
![]() по условию а) возрастает (по крайней
мере, в широком смысле) в промежутке X,
то из неравенства
по условию а) возрастает (по крайней
мере, в широком смысле) в промежутке X,
то из неравенства
![]() следует неравенство
следует неравенство
![]() .
(*)
.
(*)
Так как, по
предположению,
![]() ,
то из соотношения (*) следует, что
,
то из соотношения (*) следует, что
![]() для всех
для всех
![]() .
Но тогда, по теореме 1,
.
Но тогда, по теореме 1,
![]() ,
для всех
,
для всех
![]() .
У нас, по условию, внутри промежутка Х
не может существовать интервала
.
У нас, по условию, внутри промежутка Х
не может существовать интервала
![]() ,
во всех точках которого
,
во всех точках которого
![]() .
Следовательно, получили противоречие.
Значит, предположение, что
.
Следовательно, получили противоречие.
Значит, предположение, что
![]() неверно. Отсюда заключаем, что должно
быть
неверно. Отсюда заключаем, что должно
быть
![]() .
◄
.
◄
Замечание.
Не следует думать, что при строгом
возрастании (или строгом убывании)
функции
![]() в промежутке X
будет обязательно
в промежутке X
будет обязательно
![]() (или
(или
![]() )
во всех точках внутри промежутка X.
Например, функция
)
во всех точках внутри промежутка X.
Например, функция
![]() ,
,
![]() строго возрастает на всем бесконечном
промежутке
строго возрастает на всем бесконечном
промежутке
![]() ,
и, тем не менее,
,
и, тем не менее,
![]() обращается в нуль при
обращается в нуль при
![]() .
.
И для строго
возрастающих, и для строго убывающих
функций
![]() производная
производная
![]() в отдельных точках может обращаться в
нуль (но именно в отдельных точках, не
заполняющих никакого, хотя бы и малого
промежутка).
в отдельных точках может обращаться в
нуль (но именно в отдельных точках, не
заполняющих никакого, хотя бы и малого
промежутка).
